Giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - x + 3}}{{x + 2}}\) bằng
-
A.
\( - 1\)
-
B.
\(1\)
-
C.
\(\frac{{ - 3}}{2}\)
-
D.
\( - 3\)
Áp dụng quy tắc tính giới hạn đặc biệt: \(\mathop {\lim }\limits_{x \to \infty } \frac{1}{x} = 0\).
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - x + 3}}{{x + 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( { - 1 + \frac{3}{x}} \right)}}{{x\left( {1 + \frac{2}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1 + \frac{3}{x}}}{{1 + \frac{2}{x}}} = \frac{{ - 1 + 0}}{{1 + 0}} = - 1\).
Đáp án : A

Các bài tập cùng chuyên đề
Cho tam giác vuông OAB với \(A = \left( {a;0} \right)\) và \(B = \left( {0;1} \right)\) như Hình 5.5. Đường cao OH có độ dài là h.
a) Tính h theo a,.
b) Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao?
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H thay đổi thế nào? Tại sao?
Tính: \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 2} }}{{x + 1}}\).
Cho hàm số \(f\left( x \right) = 1 + \frac{2}{{x - 1}}\) có đồ thị như Hình 5.4.

Giả sử \(\left( {{x_n}} \right)\) là dãy số sao cho \({x_n} > 1,\;{x_n} \to \; + \infty \). Tính \(f\left( {{x_n}} \right)\) và \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } f\left( {{x_n}} \right)\).
Tính các giới hạn sau:
a) \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{1 - 2x}}{{\sqrt {{x^2} + 1} }}\)
b) \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 2} - x} \right)\)
Cho hàm số \(f\left( x \right) = \sqrt {x + 1} - \sqrt {x + 2} \). Mệnh đề đúng là
A. \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \)
B. \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0\)
C. \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - 1\)
D. \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \frac{1}{2}\)
Tính \(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 2}}{{4x - 5}}.\)
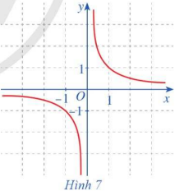
Cho hàm số \(f\left( x \right) = \frac{1}{x}\,\,\left( {x \ne 0} \right)\) có đồ thị như ở Hình 7. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
Một cái hồ đang chứa \(200{m^3}\) nước mặn với nồng độ muối \(10kg/{m^3}\). Người ta ngọt hóa nước trong hồ bằng cách bơm nước ngọt vào hồ với tốc độ \(2{m^3}/\)phút.
a) Viết biểu thức \(C\left( t \right)\) biểu thị nồng độ muối trong hồ sau \(t\) phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và giải thích ý nghĩa.
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}}\).
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.

a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng lớn (dần tới \( + \infty \))?
b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng bé (dần tới \( - \infty \))?
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{4x + 3}}{{2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{3x + 1}}\);
c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}}\).
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{\rm{x}} - 1}}{x}\) bằng:
A. 2.
B. ‒1.
C. 0.
D. 1.
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{ - x + 2}}{{x + 1}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{x - 2}}{{{x^2}}}\).
Cho hai hàm số f(x) và g(x) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 3\) và \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) + 2g\left( x \right)} \right] = 7\). Tìm \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2f\left( x \right) + g\left( x \right)}}{{2f\left( x \right) - g\left( x \right)}}\)
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{x}{{x + 4}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} + 1}}{{{{\left( {2x + 1} \right)}^2}}}\);
c) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 1}}{{\sqrt {{x^2} - 2x} }}\);
d) \(\mathop {\lim }\limits_{x \to + \infty } \left( {x - \sqrt {{x^2} + 2x} } \right)\).
Biết rằng \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2,\mathop {\lim }\limits_{x \to + \infty } \left( {f\left( x \right) + 2g\left( x \right)} \right) = 4\). Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right) - 2g\left( x \right)}}{{f\left( x \right) + 2g\left( x \right)}}\) bằng
A. \( - 1\).
B. 0.
C. \(\frac{1}{2}\).
D. \( - \frac{1}{2}\).
Biết rằng \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2ax}}{{\sqrt {{x^2} + ax} + x}} = 3\). Giá trị của a là
A. \(\frac{3}{4}\).
B. 6.
C. \(\frac{3}{2}\).
D. 3.
Với \(c\), \(k\) là các hằng số và \(k\) nguyên dương thì
A. \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = 0\)
B. \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = + \infty \)
C. \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = - \infty \)
D. \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = - \infty \)
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Phát biểu nào sau đây là đúng?
A. Nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} > a\) và \({x_n} \to + \infty \), ta có \(f\left( {{x_n}} \right) \to L\) thì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\).
B. Nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} < a\) và \({x_n} \to + \infty \), ta có \(f\left( {{x_n}} \right) \to L\) thì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\).
C. Nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} > a\), ta có \(f\left( {{x_n}} \right) \to L\) thì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\).
D. Nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} > a\) và \({x_n} \to L\), ta có \(f\left( {{x_n}} \right) \to + \infty \) thì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\).
Cho hàm số \(f\left( x \right)\) thoả mãn \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2022\). Tính \(\mathop {\lim }\limits_{x \to + \infty } \frac{{xf\left( x \right)}}{{x + 1}}\).
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\) bằng:
A. \(2\)
B. \(1\)
C. \( + \infty \)
D. \( - \infty \)
Một bể chứa 5000\(l\) nước tinh khiết. Nước muối có chứa 30 gam muối trên mỗi lít nước được bơm vào bể với tốc độ 25\(l\)/phút.
a) Chứng minh rằng nồng độ muối của nước trong bể sau \(t\) phút (tính bằng khối lượng muối chia thể tích nước trong bể, đơn vị: g/\(l\)) là \(C\left( t \right) = \frac{{30t}}{{200 + t}}\).
b) Tính \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và cho biết ý nghĩa của kết quả đó.
Cho hàm số \(f\left( x \right) = \frac{{\sqrt {{x^2} - x + 2} }}{x}\). Tính
a) \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
b) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\).
Cho hàm số \(g\left( x \right) = \sqrt {{x^2} + 2x} - \sqrt {{x^2} - 1} - 2m\) với m là tham số. Biết \(\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 0\), tìm giá trị của m.
Cho hàm số \(f\left( x \right) = \frac{{{{\sin }^2}x}}{{{x^2}}}\). Chứng minh rằng \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0\).
Một đơn vị sản xuất hàng thủ công ước tính chi phí để sản xuất x đơn vị sản phẩm là \(C\left( x \right) = 2x + 55\) (triệu đồng).
a) Tìm hàm số f(x) biểu thị chi phí trung bình để sản xuất mỗi đơn vị sản phẩm.
b) Tính \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\). Giới hạn này có ý nghĩa gì?
Biết \(\mathop {\lim }\limits_{n \to + \infty } \frac{{2{n^2} + n - 1}}{{a{n^2} + 1}} = 1\) với a là tham số. Giá trị của \({a^2} - 2a\) là
A.\( - 1\)
B. 0
C. 2
D. Không xác định
Cho hàm số \(f(x)\) thỏa mãn \(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = 2\) và \(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = m + 1\). Biết giới hạn của \(f(x)\) khi \(x \to 1\) tồn tại. Giá trị của m là
A. \(m = 1\)
B. \(m = 2\)
C. \(m = 3\)
D. Không tồn tại m.
Giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 2} - x}}{{x}}\) là
A. \( + \infty \)
B. 0
C. - 2
D. Không tồn tại.
Tìm a là số thực thỏa mãn \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{2{x^2} + 1}}{{{x^2} + 2x + 3}} + {a^2} + 3a} \right) = 0\).






