Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{x}{{x + 4}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} + 1}}{{{{\left( {2x + 1} \right)}^2}}}\);
c) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 1}}{{\sqrt {{x^2} - 2x} }}\);
d) \(\mathop {\lim }\limits_{x \to + \infty } \left( {x - \sqrt {{x^2} + 2x} } \right)\).
+ Sử dụng kiến thức về các phép toán về giới của hàm số tại vô cực để tính: Cho \(\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = L,\mathop {\lim }\limits_{x \to \pm \infty } g\left( x \right) = M\), khi đó: \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {f\left( x \right) \pm g\left( x \right)} \right] = L \pm M\), \(\mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{L}{M}\)
+ Sử dụng kiến thức về giới hạn hữu hạn cơ bản để tính: \(\mathop {\lim }\limits_{x \to \pm \infty } c = c,\mathop {\lim }\limits_{x \to \pm \infty } \frac{c}{{{x^k}}} = 0\) (với c là hằng số, k là số nguyên dương)
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{x}{{x + 4}} \) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{1 + \frac{4}{x}}} \) \( = \frac{1}{{1 + 4\mathop {\lim }\limits_{x \to + \infty } \frac{1}{x}}} \) \( = \frac{1}{{1 + 4.0}} \) \( = 1\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} + 1}}{{{{\left( {2x + 1} \right)}^2}}} \) \( = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 + \frac{1}{{{x^2}}}}}{{{{\left( {2 + \frac{1}{x}} \right)}^2}}} \) \( = \frac{{2 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{{x^2}}}}}{{{{\left( {2 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}} \right)}^2}}} \) \( = \frac{{2 + 0}}{{{{\left( {2 + 0} \right)}^2}}} \) \( = \frac{1}{2}\);
c) Với \(x < 0\) thì \(\sqrt {{x^2}} \) \( = \left| x \right| \) \( = - x\).
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 1}}{{\sqrt {{x^2} - 2x} }} \) \( = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {3 + \frac{1}{x}} \right)}}{{ - x\sqrt {1 - \frac{2}{x}} }} \) \( = \frac{{3 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}}}{{ - \sqrt {1 - \mathop {\lim }\limits_{x \to - \infty } \frac{2}{x}} }} \) \( = \frac{{3 + 0}}{{ - \sqrt {1 - 0} }} \) \( = - 3\);
d) \(\mathop {\lim }\limits_{x \to + \infty } \left( {x - \sqrt {{x^2} + 2x} } \right) \) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {x - \sqrt {{x^2} + 2x} } \right)\left( {x + \sqrt {{x^2} + 2x} } \right)}}{{x + \sqrt {{x^2} + 2x} }} \) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 2x}}{{x + \sqrt {{x^2} + 2x} }}\)
\( \) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 2}}{{1 + \sqrt {1 + \frac{2}{x}} }} \) \( = \frac{{ - 2}}{{1 + \sqrt {1 + \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x}} }} \) \( = \frac{{ - 2}}{{1 + \sqrt {1 + 0} }} \) \( = - 1\).

Các bài tập cùng chuyên đề
Cho tam giác vuông OAB với \(A = \left( {a;0} \right)\) và \(B = \left( {0;1} \right)\) như Hình 5.5. Đường cao OH có độ dài là h.
a) Tính h theo a,.
b) Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao?
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H thay đổi thế nào? Tại sao?
Tính: \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 2} }}{{x + 1}}\).
Cho hàm số \(f\left( x \right) = 1 + \frac{2}{{x - 1}}\) có đồ thị như Hình 5.4.

Giả sử \(\left( {{x_n}} \right)\) là dãy số sao cho \({x_n} > 1,\;{x_n} \to \; + \infty \). Tính \(f\left( {{x_n}} \right)\) và \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } f\left( {{x_n}} \right)\).
Tính các giới hạn sau:
a) \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{1 - 2x}}{{\sqrt {{x^2} + 1} }}\)
b) \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 2} - x} \right)\)
Cho hàm số \(f\left( x \right) = \sqrt {x + 1} - \sqrt {x + 2} \). Mệnh đề đúng là
A. \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \)
B. \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0\)
C. \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - 1\)
D. \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \frac{1}{2}\)
Tính \(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 2}}{{4x - 5}}.\)
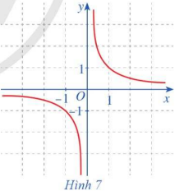
Cho hàm số \(f\left( x \right) = \frac{1}{x}\,\,\left( {x \ne 0} \right)\) có đồ thị như ở Hình 7. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
Một cái hồ đang chứa \(200{m^3}\) nước mặn với nồng độ muối \(10kg/{m^3}\). Người ta ngọt hóa nước trong hồ bằng cách bơm nước ngọt vào hồ với tốc độ \(2{m^3}/\)phút.
a) Viết biểu thức \(C\left( t \right)\) biểu thị nồng độ muối trong hồ sau \(t\) phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và giải thích ý nghĩa.
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}}\).
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.

a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng lớn (dần tới \( + \infty \))?
b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng bé (dần tới \( - \infty \))?
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{4x + 3}}{{2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{3x + 1}}\);
c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}}\).
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{\rm{x}} - 1}}{x}\) bằng:
A. 2.
B. ‒1.
C. 0.
D. 1.
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{ - x + 2}}{{x + 1}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{x - 2}}{{{x^2}}}\).
Cho hai hàm số f(x) và g(x) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 3\) và \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) + 2g\left( x \right)} \right] = 7\). Tìm \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2f\left( x \right) + g\left( x \right)}}{{2f\left( x \right) - g\left( x \right)}}\)
Biết rằng \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2,\mathop {\lim }\limits_{x \to + \infty } \left( {f\left( x \right) + 2g\left( x \right)} \right) = 4\). Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right) - 2g\left( x \right)}}{{f\left( x \right) + 2g\left( x \right)}}\) bằng
A. \( - 1\).
B. 0.
C. \(\frac{1}{2}\).
D. \( - \frac{1}{2}\).
Biết rằng \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2ax}}{{\sqrt {{x^2} + ax} + x}} = 3\). Giá trị của a là
A. \(\frac{3}{4}\).
B. 6.
C. \(\frac{3}{2}\).
D. 3.
Với \(c\), \(k\) là các hằng số và \(k\) nguyên dương thì
A. \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = 0\)
B. \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = + \infty \)
C. \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = - \infty \)
D. \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = - \infty \)
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Phát biểu nào sau đây là đúng?
A. Nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} > a\) và \({x_n} \to + \infty \), ta có \(f\left( {{x_n}} \right) \to L\) thì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\).
B. Nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} < a\) và \({x_n} \to + \infty \), ta có \(f\left( {{x_n}} \right) \to L\) thì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\).
C. Nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} > a\), ta có \(f\left( {{x_n}} \right) \to L\) thì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\).
D. Nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} > a\) và \({x_n} \to L\), ta có \(f\left( {{x_n}} \right) \to + \infty \) thì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\).
Cho hàm số \(f\left( x \right)\) thoả mãn \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2022\). Tính \(\mathop {\lim }\limits_{x \to + \infty } \frac{{xf\left( x \right)}}{{x + 1}}\).
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\) bằng:
A. \(2\)
B. \(1\)
C. \( + \infty \)
D. \( - \infty \)
Một bể chứa 5000\(l\) nước tinh khiết. Nước muối có chứa 30 gam muối trên mỗi lít nước được bơm vào bể với tốc độ 25\(l\)/phút.
a) Chứng minh rằng nồng độ muối của nước trong bể sau \(t\) phút (tính bằng khối lượng muối chia thể tích nước trong bể, đơn vị: g/\(l\)) là \(C\left( t \right) = \frac{{30t}}{{200 + t}}\).
b) Tính \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và cho biết ý nghĩa của kết quả đó.
Cho hàm số \(f\left( x \right) = \frac{{\sqrt {{x^2} - x + 2} }}{x}\). Tính
a) \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
b) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\).
Cho hàm số \(g\left( x \right) = \sqrt {{x^2} + 2x} - \sqrt {{x^2} - 1} - 2m\) với m là tham số. Biết \(\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 0\), tìm giá trị của m.
Cho hàm số \(f\left( x \right) = \frac{{{{\sin }^2}x}}{{{x^2}}}\). Chứng minh rằng \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0\).
Một đơn vị sản xuất hàng thủ công ước tính chi phí để sản xuất x đơn vị sản phẩm là \(C\left( x \right) = 2x + 55\) (triệu đồng).
a) Tìm hàm số f(x) biểu thị chi phí trung bình để sản xuất mỗi đơn vị sản phẩm.
b) Tính \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\). Giới hạn này có ý nghĩa gì?
Biết \(\mathop {\lim }\limits_{n \to + \infty } \frac{{2{n^2} + n - 1}}{{a{n^2} + 1}} = 1\) với a là tham số. Giá trị của \({a^2} - 2a\) là
A.\( - 1\)
B. 0
C. 2
D. Không xác định
Cho hàm số \(f(x)\) thỏa mãn \(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = 2\) và \(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = m + 1\). Biết giới hạn của \(f(x)\) khi \(x \to 1\) tồn tại. Giá trị của m là
A. \(m = 1\)
B. \(m = 2\)
C. \(m = 3\)
D. Không tồn tại m.
Giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 2} - x}}{{x}}\) là
A. \( + \infty \)
B. 0
C. - 2
D. Không tồn tại.
Tìm a là số thực thỏa mãn \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{2{x^2} + 1}}{{{x^2} + 2x + 3}} + {a^2} + 3a} \right) = 0\).
Nghiên cứu về quá trình tăng trưởng của một quần thể sinh vật trong điều kiện môi trường sống hạn chế cho thấy: ban đầu số lượng cá thể tăng trưởng chậm, sau đó nhanh và cuối cùng khi thời gian đủ dài, số lượng cá thể của quần thể đạt đến trạng thái cân bằng, khi đó số lượng cá thể sinh ra xấp xỉ bằng số lượng chết đi. Số lượng cá thể \(N\) trong quần thể theo thời gian \(t\) (ngày) được mô hình hóa và xấp xỉ theo hàm số: \(N\left( t \right) = \frac{{16398{e^{0,5\left( {t - 9,19} \right)}}}}{{0,12 + {e^{0,5\left( {t - 9,19} \right)}}}}\). Khi quần thể sinh vật trên đạt trạng thái cân bằng, số cá thể của quần thể gần nhất với giá trị nào sau đây?
-
A.
9264
-
B.
136650
-
C.
16398
-
D.
224630







Danh sách bình luận