Cho tam giác ABC có M, N lần lượt là trung điểm của AC, BC.
a) Chứng minh tứ giác AMNB là hình thang.
b) Gọi I là giao điểm của AN và BM. Trên tia đối của tia NA lấy điểm E sao cho \(NE = NI\). Trên tia đối của tia MB lấy điểm F sao cho \(MF = MI\). Chứng minh EF//AB.
+ Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+ Sử dụng kiến thức về tính chất của đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
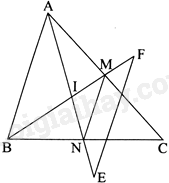
a) Xét tam giác ABC có: \(MA = MC,NB = NC\) nên MN là đường trung bình của tam giác ABC, suy ra MN//AB, suy ra tứ giác AMNB là hình thang.
b) Xét tam giác IEF có: \(NE = NI\), \(MF = MI\) nên MN là đường trung bình của tam giác EIF, suy ra MN//EF
Mà MN//AB, suy ra EF//AB.

Các bài tập cùng chuyên đề
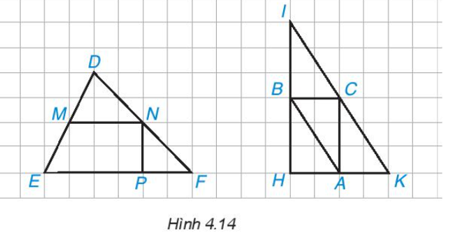
Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
Mỗi tam giác có bao nhiêu đường trung bình?
A. 1.
B. 2.
C. 3.
D. 4.
Trong Hình 5, chứng minh \(MN\) là đường trung bình của tam giác \(ABC\).

Quan sát ta, giác ABC ở Hình 29 và cho biết hai đầu mút D, E của đoạn thẳng DE có đặc điểm gì.

Vẽ tam giác ABC và các đường trung bình của tam giác đó.
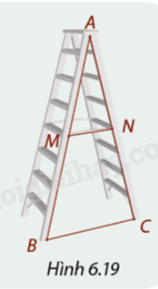
Trong Hình 6.19, để thang xếp đứng vững, hai chân \(AB\) và \(AC\) của nó được nối với nhau bằng thanh khóa \(MN.\) So sánh các đoạn thẳng \(AM\) và \(BN,AN\) và \(CN,\) em có nhận xét gì về vị trí điểm \(M\) và \(N\) trên cạnh \(AB\) và \(AC\) của tam giác \(ABC?\)
Vẽ tam giác \(MNP\) bất kì và vẽ các đường trung bình của nó.
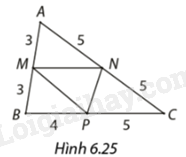
Đoạn thẳng nào trong các đoạn thẳng \(MN,NP,MP\) là đường trung bình của tam giác \(ABC\) trong hình 6.25?
-
A.
trung điểm của hai cạnh của một tam giác.
-
B.
trung điểm của một cạnh của một tam giác.
-
C.
hai đỉnh của một tam giác.
-
D.
một đỉnh và một trung điểm của một cạnh của một tam giác.
Đường trung bình của tam giác là đoạn thẳng đi qua
-
A.
trung điểm một cạnh của tam giác đó.
-
B.
trung điểm hai cạnh của tam giác đó.
-
C.
hai đỉnh của tam giác đó.
-
D.
một đỉnh và một trung điểm của cạnh đối diện của tam giác đó.
Cho hình vẽ bên. Khẳng định nào sau đây đúng về \(MN\)?
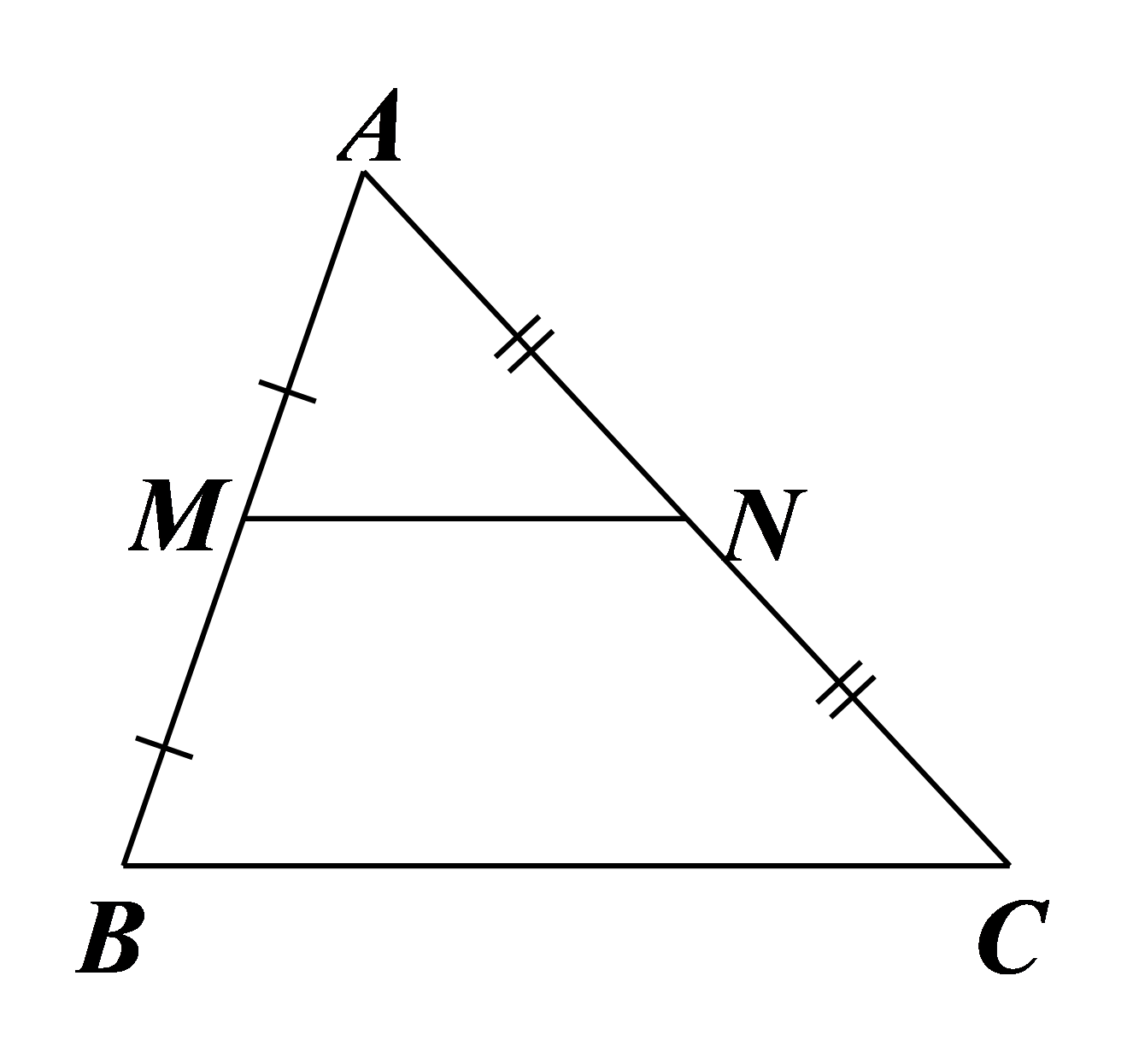
-
A.
Là đường trung tuyến của \(\Delta ABC\).
-
B.
Là đường trung bình của \(\Delta ABC\).
-
C.
Là đường trung trực của \(\Delta ABC\).
-
D.
Là đường phân giác của \(\Delta ABC\).
Cho hình vẽ bên. Khẳng định nào sau đây là đúng về \(MN\)?
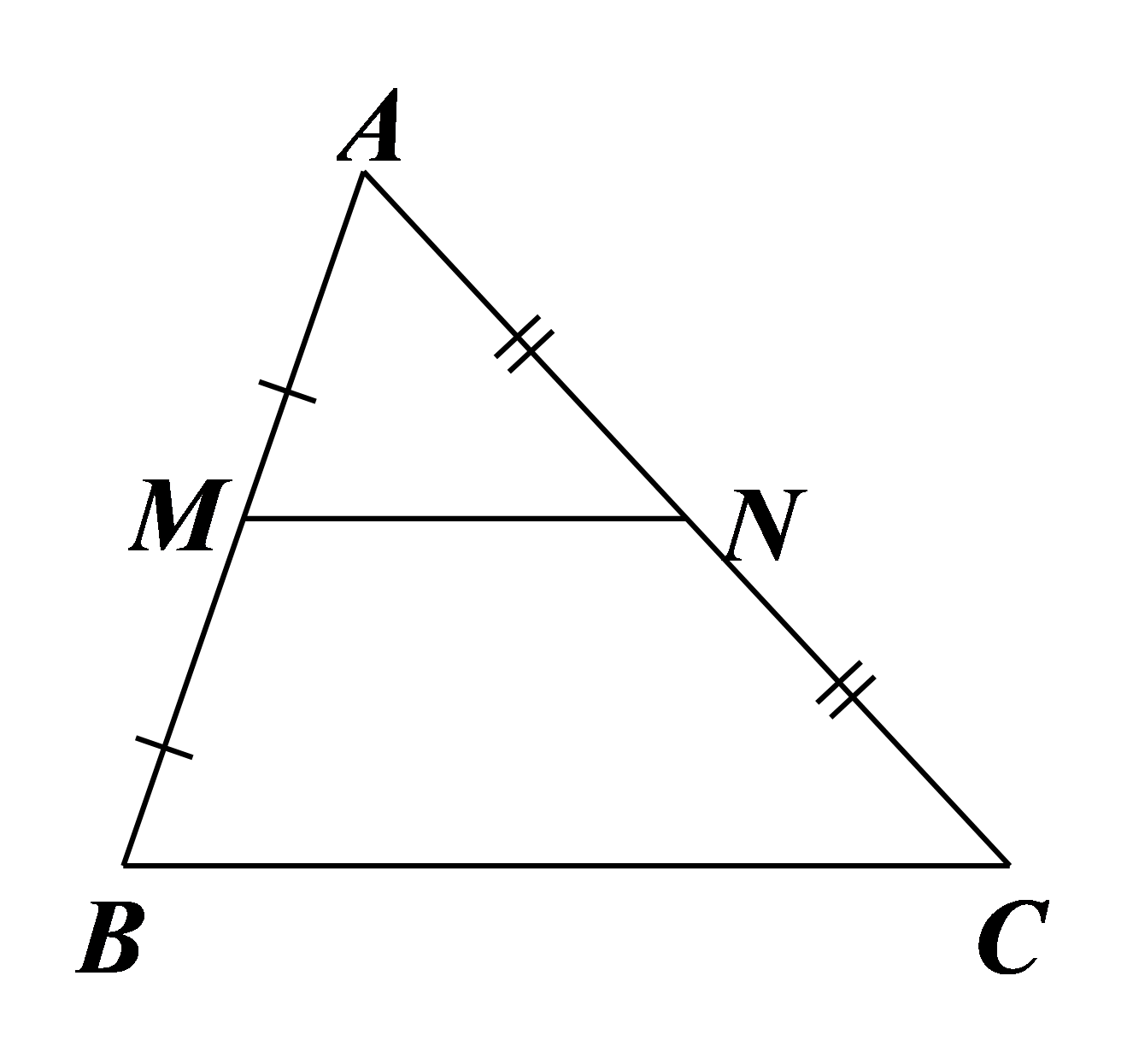
-
A.
Là đường trung tuyến của \(\Delta ABC\)
-
B.
Là đường trung bình của \(\Delta ABC\)
-
C.
Là đường trung trực của \(\Delta ABC\)
-
D.
Là đường phân giác của \(\Delta ABC\)
Một tam giác có bao nhiêu đường trung bình?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Cho hình vẽ: Đoạn thẳng nào là đường trung bình của tam giác ABC?
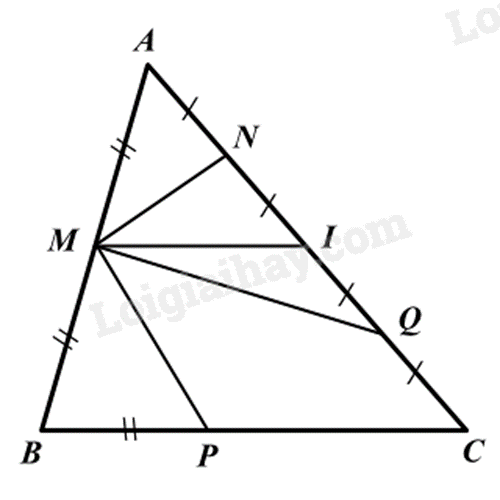
-
A.
MP.
-
B.
MN.
-
C.
MI.
-
D.
MQ.
Cho các hình sau:
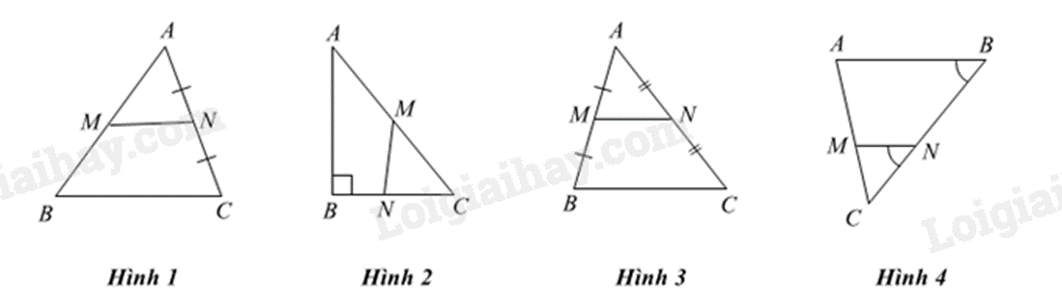
Đoạn thẳng MN là đường trung bình của tam giác ABC trong hình vẽ nào?
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.







Danh sách bình luận