Cho hàm số \(y = \dfrac{{x - 2}}{{x + 1}}\) có đồ thị \(\left( C \right).\) Gọi \(I\) là giao điểm của hai tiệm cận của \(\left( C \right).\) Xét tam giác đều \(ABI\) có hai đỉnh \(A,\;B\) thuộc \(\left( C \right),\) đoạn thẳng \(AB\) có độ dài bằng:
-
A.
\(2\sqrt 3 \)
-
B.
\(2\sqrt 2 \)
-
C.
\(\sqrt 3 \)
-
D.
\(\sqrt 6 \)
- Viết phương trình đường thẳng \(AB\)
- Tính khoảng cách \(AB\) và sử dụng tính chất tam giác đều \(d\left( {I,AB} \right) = \dfrac{{AB\sqrt 3 }}{2}\)
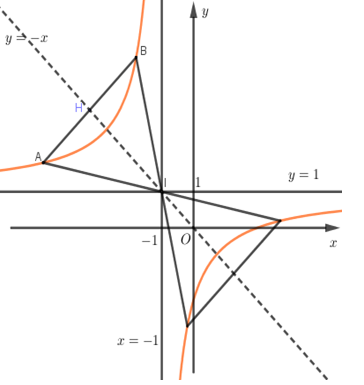
Ta có: \(x = - 1\) là TCĐ của đồ thị hàm số, \(y = 1\) là TCN của đồ thị hàm số.
\( \Rightarrow I\left( { - 1;\;1} \right)\) là giao điểm của hai đường tiệm cận của đồ thị hàm số.
Dựa vào đồ thị hàm số ta có \(\Delta IAB\) là tam giác đều
\( \Rightarrow IH\) vừa là đường cao đồng thời là đường phân giác của \(\angle AIB \Rightarrow IH\) cũng là đường phân giác của góc phần tư thứ hai.
\( \Rightarrow IH:\;\;y = - x.\)
Ta có: \(AB \bot IH \Rightarrow AB:\;\;y = x + m \Leftrightarrow x - y + m = 0.\)
\( \Rightarrow d\left( {I;\;AB} \right) = \dfrac{{\left| { - 1 - 1 + m} \right|}}{{\sqrt 2 }} = \dfrac{{\left| {m - 2} \right|}}{{\sqrt 2 }}.\)
Xét phương trình hoành độ giao điểm: \(\dfrac{{x - 2}}{{x + 1}} = x + m \Leftrightarrow {x^2} + mx + m + 2 = 0\)
Phương trình có hai nghiệm phân biệt \( \Leftrightarrow {m^2} - 4\left( {m + 2} \right) > 0 \Leftrightarrow {m^2} - 4m > 8\)
Khi đó hoành độ các giao điểm \(A,\;B\) là nghiệm của phương trình trên.
Gọi \(A\left( {{x_1};\;{x_1} + m} \right);B\left( {{x_2};\;{x_2} + m} \right)\)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - m\\{x_1}{x_2} = m + 2\end{array} \right..\)
\( \Rightarrow A{B^2} = {\left( {{x_1} - {x_2}} \right)^2} + {\left( {{x_1} + m - {x_2} - m} \right)^2}\) \( = 2{\left( {{x_1} - {x_2}} \right)^2} = 2{\left( {{x_1} + {x_2}} \right)^2} - 8{x_1}{x_2}\) \( = 2{m^2} - 8\left( {m + 2} \right)\)
Do tam giác \(IAB\) đều nên \(d\left( {I,AB} \right) = \dfrac{{AB\sqrt 3 }}{2}\) \( \Leftrightarrow {d^2}\left( {I,AB} \right) = \dfrac{{3A{B^2}}}{4}\)
\( \Leftrightarrow \dfrac{{{{\left( {m - 2} \right)}^2}}}{2} = \dfrac{{3\left[ {2{m^2} - 8\left( {m + 2} \right)} \right]}}{4}\) $ \Leftrightarrow {m^2} - 4m = 14$ (thỏa điều kiện \({m^2} - 4m > 8\))
$ \Rightarrow AB = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2}} $ $ = \sqrt {2{m^2} - 8\left( {m + 2} \right)} $ $ = \sqrt {2\left( {{m^2} - 4m - 8} \right)} $ \( = \sqrt {2.\left( {14 - 8} \right)} = \sqrt {12} = 2\sqrt 3 .\)
Đáp án : A

Các bài tập cùng chuyên đề
Tìm giá trị nhỏ nhất của hàm số \(y = \left| {\sin x + \cos x + \tan x + \cot x + \dfrac{1}{{\sin x}} + \dfrac{1}{{\cos x}}} \right|\)
Biết rằng đồ thị hàm số bậc 4: \(y = f\left( x \right)\) được cho như hình vẽ sau:
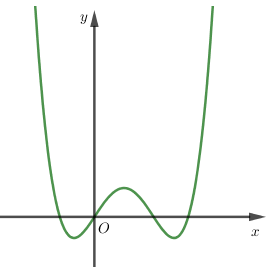
Tìm số giao điểm của đồ thị hàm số \(y = g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right)\) và trục $Ox.$
Với điều kiện \(\left\{ \begin{array}{l}ac\left( {{b^2} - 4ac} \right) > 0\\ab < 0\end{array} \right.\) thì đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) cắt trục hoành tại bao nhiêu điểm?
Cho hàm số $f(x) = {x^3} + a{x^2} + bx - 2$ thỏa mãn $\left\{ \begin{array}{l}a + b > 1\\3 + 2a + b < 0\end{array} \right.$. Số điểm cực trị của hàm số $y = \left| {f\left( {\left| x \right|} \right)} \right|$ bằng:
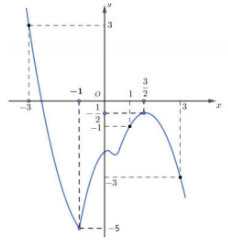
Cho hàm số $y = f(x)$ có đồ thị hàm số $f'(x)$ như hình vẽ. Hàm số $y = f(1 - x) + \dfrac{{{x^2}}}{2} - x$ nghịch biến trên khoảng
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = {x^8} + \left( {m - 2} \right){x^5} - \left( {{m^2} - 4} \right){x^4} + 1\) đạt cực tiểu tại \(x = 0\)?
Cho hàm số \(y = \dfrac{1}{6}{x^4} - \dfrac{7}{3}{x^2}\) có đồ thị hàm số \(\left( C \right).\) Có bao nhiêu điểm \(A\) thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(A\) cắt \(\left( C \right)\) tại hai điểm phân biệt \(M\left( {{x_1};\;{y_1}} \right),\;N\left( {{x_2};\;{y_2}} \right)\;\;\left( {M,\;N \ne A} \right)\) thỏa mãn \({y_1} - {y_2} = 4\left( {{x_1} - {x_2}} \right)?\)
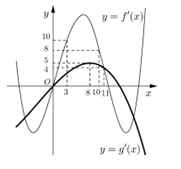
Cho hai hàm số \(y = f\left( x \right),\;y = g\left( x \right).\) Hai hàm số \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị hàm như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right).\) Hàm số \(h\left( x \right) = f\left( {x + 6} \right) - g\left( {2x + \dfrac{5}{2}} \right)\) đồng biến trên khoảng nào dưới đây?
Cho hàm số \(f\left( x \right) = {x^3} - 6{x^2} + 9x\). Đặt \({f^k}\left( x \right) = f\left( {{f^{k - 1}}\left( x \right)} \right)\) (với $k$ là số tự nhiên lớn hơn $1$). Tính số nghiệm của phương trình \({f^8}\left( x \right) = 0\)
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 7} \right)\left( {{x^2} - 9} \right),\,\forall \,x \in \,\mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {\left| {{x^3} + 5x} \right| + m} \right)\) có ít nhất 3 điểm cực trị?






