Cho hàm số $f(x) = {x^3} + a{x^2} + bx - 2$ thỏa mãn $\left\{ \begin{array}{l}a + b > 1\\3 + 2a + b < 0\end{array} \right.$. Số điểm cực trị của hàm số $y = \left| {f\left( {\left| x \right|} \right)} \right|$ bằng:
-
A.
$5$
-
B.
$9$
-
C.
$2$
-
D.
$11$
- Tìm số giao điểm của đồ thị hàm số đã cho với \(Ox\), sử dụng kiến thức:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {a;b} \right)\). Nếu \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất \(1\) nghiệm \({x_0} \in \left( {a;b} \right)\)
- Vẽ phác dáng đồ thị hàm số \(y = f\left( x \right)\)
- Vẽ dáng đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có được từ đồ thị hàm số \(y = f\left( x \right)\)
- Vẽ dáng đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) và kết luận số điểm cực trị của hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\)
Ta có: $f(x) = {x^3} + a{x^2} + bx - 2$
$ + )f\left( 0 \right) = - 2 < 0;$ $f(1) = a + b - 1 > 0$ nên \(f\left( 0 \right).f\left( 1 \right) < 0\)
\( \Rightarrow \) phương trình \(f\left( x \right) = 0\) có ít nhất \(1\) nghiệm \({x_1} \in \left( {0;1} \right)\)
\( + )f\left( 2 \right) = 2\left( {3 + 2a + b} \right) < 0\) nên \(f\left( 1 \right).f\left( 2 \right) < 0\)
\( \Rightarrow \) phương trình \(f\left( x \right) = 0\) có ít nhất \(1\) nghiệm \({x_2} \in \left( {1;2} \right)\)
Do đó phương trình \(f\left( x \right) = 0\) có ít nhất hai nghiệm và đồ thị hàm số \(y = f\left( x \right)\) chỉ có thể có dạng:
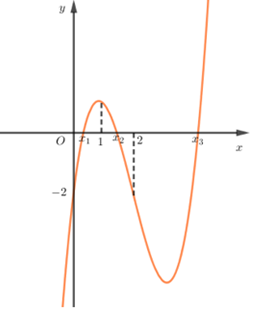
Khi đó, đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\)(màu tím) và \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) (màu cam) lần lượt có đồ thị như sau:
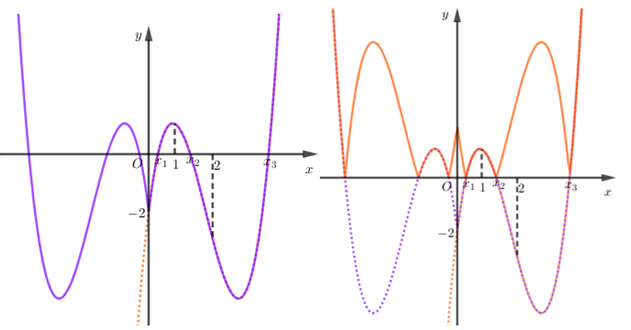
Như vậy, hàm số $y = \left| {f\left( {\left| x \right|} \right)} \right|$ có tất cả $11$ cực trị.
Đáp án : D
Các bài tập cùng chuyên đề
Tìm giá trị nhỏ nhất của hàm số \(y = \left| {\sin x + \cos x + \tan x + \cot x + \dfrac{1}{{\sin x}} + \dfrac{1}{{\cos x}}} \right|\)
Biết rằng đồ thị hàm số bậc 4: \(y = f\left( x \right)\) được cho như hình vẽ sau:
Tìm số giao điểm của đồ thị hàm số \(y = g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right)\) và trục $Ox.$
Với điều kiện \(\left\{ \begin{array}{l}ac\left( {{b^2} - 4ac} \right) > 0\\ab < 0\end{array} \right.\) thì đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) cắt trục hoành tại bao nhiêu điểm?
Cho hàm số $y = f(x)$ có đồ thị hàm số $f'(x)$ như hình vẽ. Hàm số $y = f(1 - x) + \dfrac{{{x^2}}}{2} - x$ nghịch biến trên khoảng
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = {x^8} + \left( {m - 2} \right){x^5} - \left( {{m^2} - 4} \right){x^4} + 1\) đạt cực tiểu tại \(x = 0\)?
Cho hàm số \(y = \dfrac{{x - 2}}{{x + 1}}\) có đồ thị \(\left( C \right).\) Gọi \(I\) là giao điểm của hai tiệm cận của \(\left( C \right).\) Xét tam giác đều \(ABI\) có hai đỉnh \(A,\;B\) thuộc \(\left( C \right),\) đoạn thẳng \(AB\) có độ dài bằng:
Cho hàm số \(y = \dfrac{1}{6}{x^4} - \dfrac{7}{3}{x^2}\) có đồ thị hàm số \(\left( C \right).\) Có bao nhiêu điểm \(A\) thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(A\) cắt \(\left( C \right)\) tại hai điểm phân biệt \(M\left( {{x_1};\;{y_1}} \right),\;N\left( {{x_2};\;{y_2}} \right)\;\;\left( {M,\;N \ne A} \right)\) thỏa mãn \({y_1} - {y_2} = 4\left( {{x_1} - {x_2}} \right)?\)
Cho hai hàm số \(y = f\left( x \right),\;y = g\left( x \right).\) Hai hàm số \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị hàm như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right).\) Hàm số \(h\left( x \right) = f\left( {x + 6} \right) - g\left( {2x + \dfrac{5}{2}} \right)\) đồng biến trên khoảng nào dưới đây?
Cho hàm số \(f\left( x \right) = {x^3} - 6{x^2} + 9x\). Đặt \({f^k}\left( x \right) = f\left( {{f^{k - 1}}\left( x \right)} \right)\) (với $k$ là số tự nhiên lớn hơn $1$). Tính số nghiệm của phương trình \({f^8}\left( x \right) = 0\)
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 7} \right)\left( {{x^2} - 9} \right),\,\forall \,x \in \,\mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {\left| {{x^3} + 5x} \right| + m} \right)\) có ít nhất 3 điểm cực trị?
