Cho hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm. Tính \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right|\).
Cho hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm. Tính \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right|\).
-
A.
5 cm
-
B.
7 cm
-
C.
9 cm
-
D.
11 cm
Sử dụng quy tắc hình bình hành và định lí Pythagore.
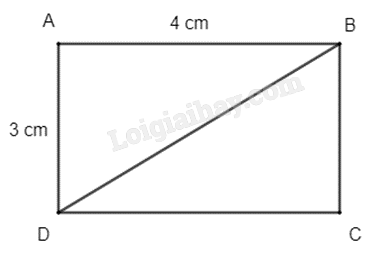
Vì ABCD là hình chữ nhật nên đồng thời là hình bình hành. Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow {BC} + \overrightarrow {BA} = \overrightarrow {BD} \).
Suy ra, \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right| = \left| {\overrightarrow {BD} } \right| = BD\).
Áp dụng định lí Pythagore trong tam giác vuông ABD:
\(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{4^2} + {3^2}} = 5\) (cm).
Vậy \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right| = \left| {\overrightarrow {BD} } \right| = BD\) = 5 cm.
Đáp án : A
Các bài tập cùng chuyên đề
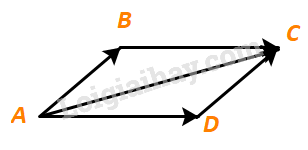
Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)
Hãy giải thích hướng đi của thuyền ở Hình 48.
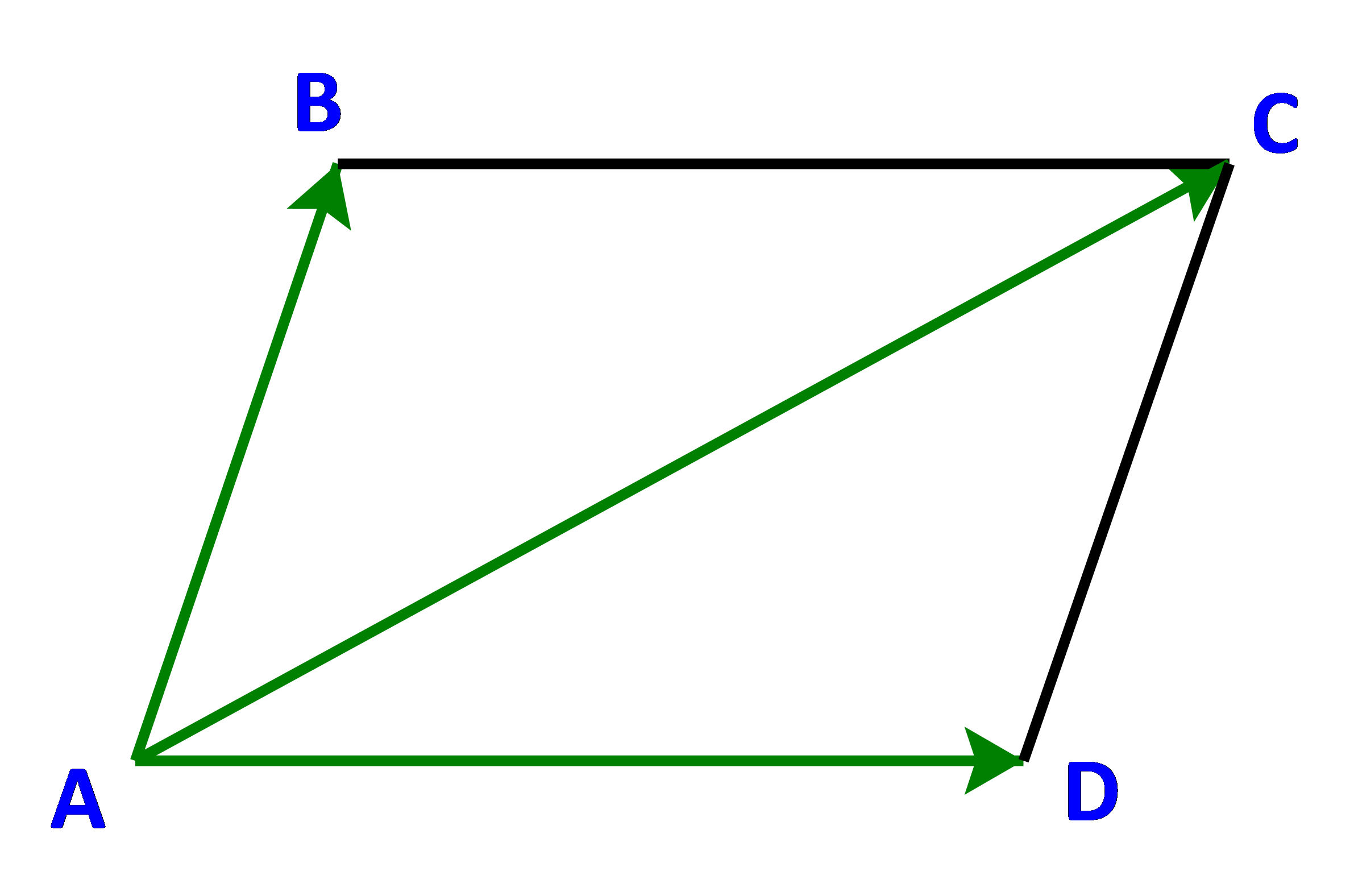
Cho ABCD là hình bình hành (Hình 52). So sánh:
a) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
b) Vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \) và vecto \(\overrightarrow {AC} \)
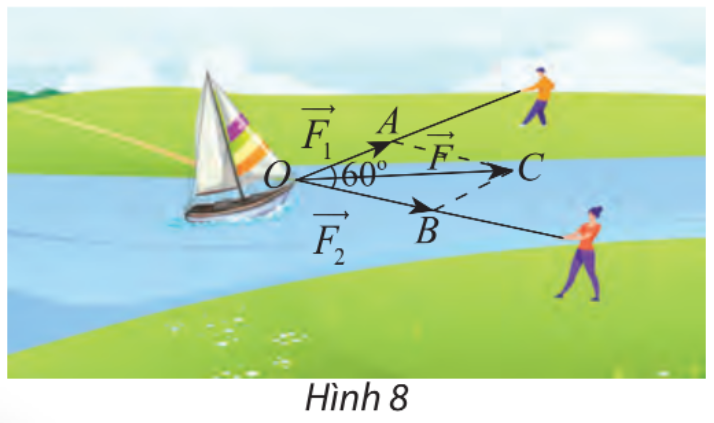
Hai người cùng kéo một con thuyền với hai lực \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} \) có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là \({60^\circ }\). Tìm độ lớn của vectơ hợp lực \(\overrightarrow F \) là tổng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \)
Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC}\)
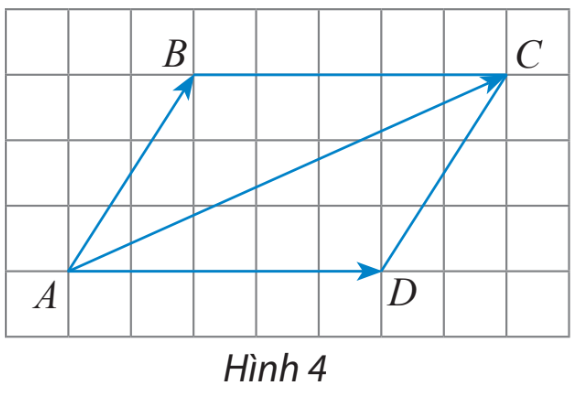
Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {CA} \)
B. \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} \)
C. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {CA} \)
D. \(\overrightarrow {AB} + \overrightarrow {BC} = - \overrightarrow {AC} \)
Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} \)
B. \(\overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} \)
C. \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {CD} \)
D. \(\overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {CD} \)
Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ \(\overrightarrow {OM} \).
