Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC}\)
Bước 1: Dựng hình bình hành ABDC
Bước 2: Áp dụng quy tắc hình bình hành tìm tổng vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \)
Bước 3: Tìm độ dài vectơ tổng.
Dựng hình bình hành ABDC.
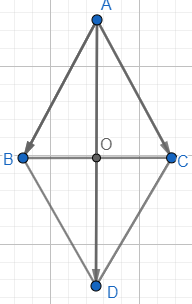
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)
Các bài tập cùng chuyên đề
Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)
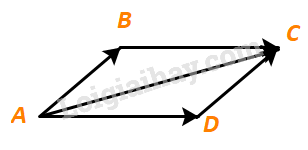
Hãy giải thích hướng đi của thuyền ở Hình 48.
Cho ABCD là hình bình hành (Hình 52). So sánh:
a) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
b) Vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \) và vecto \(\overrightarrow {AC} \)
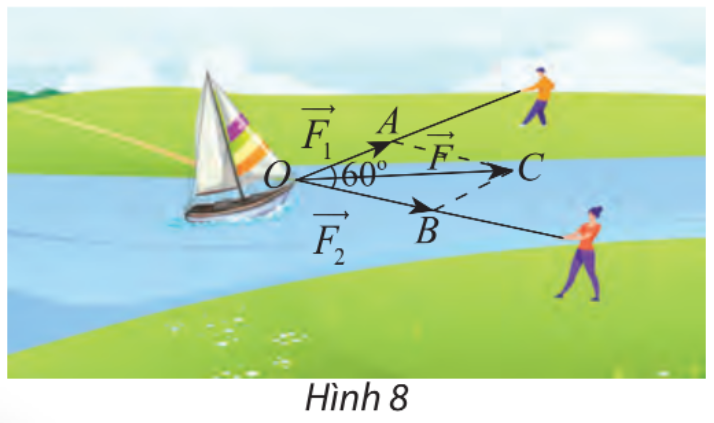
Hai người cùng kéo một con thuyền với hai lực \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} \) có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là \({60^\circ }\). Tìm độ lớn của vectơ hợp lực \(\overrightarrow F \) là tổng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \)
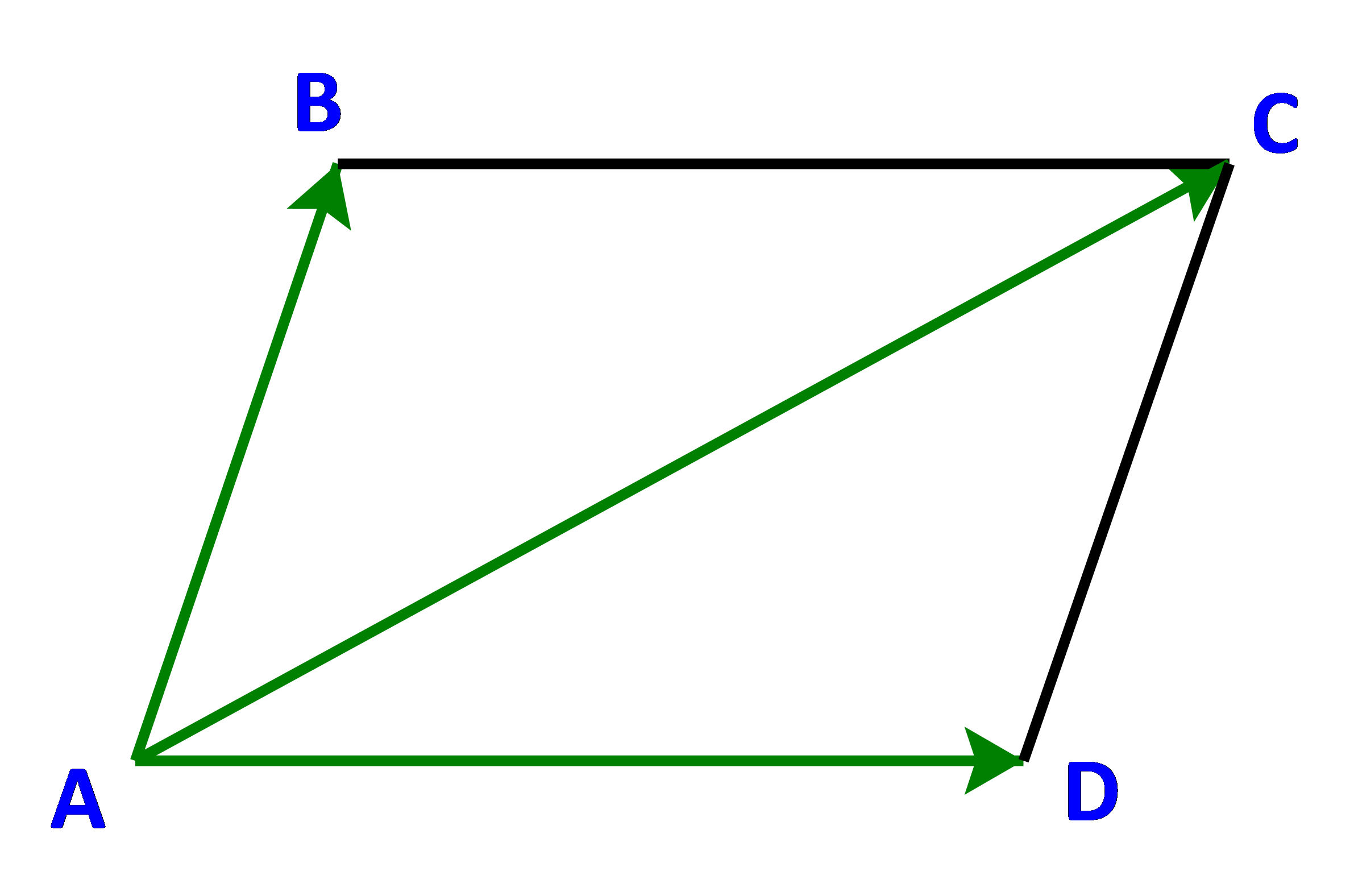
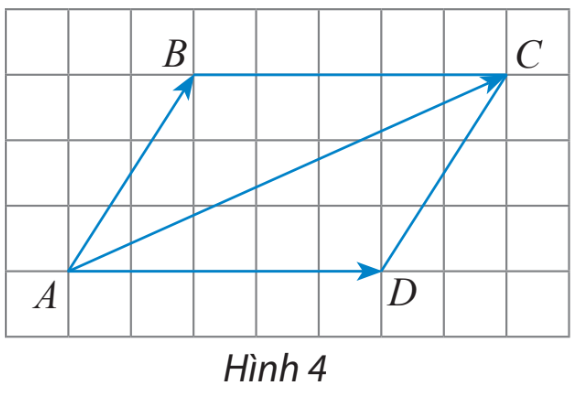
Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {CA} \)
B. \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} \)
C. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {CA} \)
D. \(\overrightarrow {AB} + \overrightarrow {BC} = - \overrightarrow {AC} \)
Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} \)
B. \(\overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} \)
C. \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {CD} \)
D. \(\overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {CD} \)
Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ \(\overrightarrow {OM} \).
Cho hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm. Tính \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right|\).
-
A.
5 cm
-
B.
7 cm
-
C.
9 cm
-
D.
11 cm
