Cho $\Delta ABC$ đều có cạnh $3cm$ ngoại tiếp đường tròn $\left( O,r \right)$. Tính $r$
-
A.
$2\sqrt{3}$
-
B.
$3\sqrt{3}$
-
C.
$\frac{3\sqrt{3}}{2}$
-
D.
$\frac{\sqrt{3}}{2}$
Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng $\frac{a\sqrt{3}}{6}$.
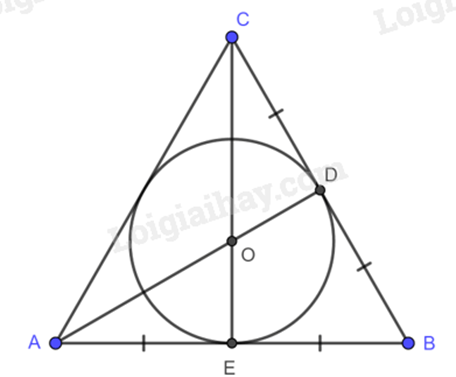
Bán kính đường tròn nội tiếp tam giác đều ABC là:
$r=\frac{3\sqrt{3}}{6}=\frac{\sqrt{3}}{2}$.
Đáp án D
Đáp án : D

Các bài tập cùng chuyên đề
Cho tam giác ABC có I là giao điểm của ba đường phân giác. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hình 12).
a) So sánh các đoạn thẳng IM, IN, IP.
b) Đặt r = IM. Đường tròn (I; r) có phải là đường tròn nội tiếp tam giác ABC hay không? Vì sao?
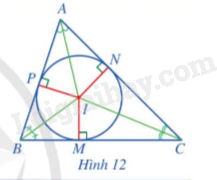
Tâm đường tròn nội tiếp của một tam giác là giao của các đường
-
A.
trung trực.
-
B.
phân giác.
-
C.
trung tuyến.
-
D.
đường cao.
Cho lục giác đều ABCDEF cạnh bằng a.
a) Chứng minh sáu điểm A, B, C, D, E, F cùng thuộc một đường tròn. Tính theo a bán kính của đường tròn đó.
b) Chứng minh các tam giác ACE, BFD là các tam giác đều. Tính theo a bán kính đường tròn nội tiếp tương ứng của tam giác đó.
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến MA và MB với đường tròn đó (A, B là các tiếp điểm) sao cho MA = \(R\sqrt 3 \)
a) Xác định tâm và bán kính đường tròn nội tiếp tam giác MAB.
b) Tính chu vi tam giác MAB.
c) Vẽ đường thẳng d đi qua M cắt đường tròn (O) tại hai điểm P, Q. Xác định vị trí của đường thẳng d sao cho MQ + MP đạt giá trị nhỏ nhất.
Cho tam giác ABC vuông tại A có \(AB = 4cm,AC = 6cm\). Tính bán kính của đường tròn nội tiếp tam giác ABC.
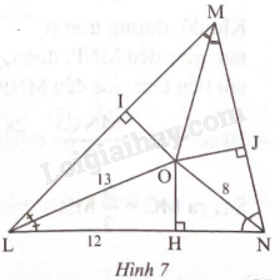
Một công viên hình tam giác được bao quanh bởi ba con đường ML, LN, NM với kích thước (tính theo mét) được ghi trên bản vẽ trong Hình 7. Người ta muốn dựng một trụ đèn tại một điểm cách đều ba con đường. Xác định vị trí điểm cần tìm và tính khoảng cách từ điểm đó đến ba con đường.
Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1cm.
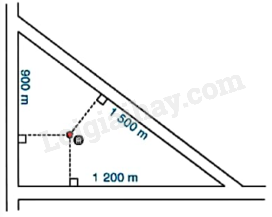
Người ta vẽ bản quy hoạch của một khu dân cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900m, 1 200m và 1 500m như hình vẽ dưới đây.
a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên.
b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
Cho tam giác ABC là tam giác vuông tại đỉnh A và nội tiếp đường tròn (O) có bán kính 5cm. Biết rằng diện tích tam giác ABC bằng \(24c{m^2}\). Tính bán kính đường tròn nội tiếp của tam giác ABC.
Cho tam giác ABC, gọi G là giao điểm ba đường phân giác của tam giác đó. Từ G kẻ GH, GI, GK lần lượt vuông góc với AB, AC, BC (\(H \in AB,I \in AC,K \in BC\)). So sánh độ dài GH, GI, GK.
-
A.
GH < GI < GK.
-
B.
GH = GI = GK.
-
C.
GH > GI > GK.
-
D.
GH = GI > GK.







Danh sách bình luận