Một hình hộp chữ nhật có thể tích là \({x^3} + 6{x^2} + 11x + 6\)\((c{m^3})\). Biết đáy là hình chữ nhật có các kích thước là \(x + 1\)(cm) và \(x + 2\)(cm). Tính chiều cao của hình hộp chữ nhật đó theo x.
Thể tích hình hộp chữ nhật bằng diện tích đáy nhân chiều cao.
Để tính chiều chiều cao của hình hộp chữ nhật, ta lấy thể tích hình hộp chữ nhật chia cho diện tích đáy. (Trong bài trên, diện tích đáy của hình hộp chữ nhật là hình chữ nhật và bằng chiều dài nhân chiều rộng hay bằng tích của 2 cạnh).
Diện tích mặt đáy của hình hộp chữ nhật là:
\((x + 1).(x + 2) = x(x + 2) + 1.(x + 2)\\ = {x^2} + 2x + x + 2 = {x^2} + 3x + 2\) \((c{m^2})\).
Vậy chiều cao của hình hộp chữ nhật đó theo x là:
\(({x^3} + 6{x^2} + 11x + 6):({x^2} + 3x + 2) = x + 3\)(cm).

Các bài tập cùng chuyên đề
Kiểm tra lại rằng ta có phép chia hết A : B = 2x2 – 5x + 1, nghĩa là xảy ra A = B . (2x2 – 5x + 1)
Thực hiện phép chia:
a) (-x6 + 5x4 – 2x3) : (0,5x2)
b) (9x2 – 4) : (3x + 2)
Vận dụng giải bài toán tròn tính huống mở đầu
Tìm đa thức P sao cho A = B. P, trong đó A = 2x4 – 3x3 – 3x2 + 6x – 2 và B = x2 – 2
Thực hiện các phép chia đa thức sau:
a) (-5x3 + 15x2 + 18x) : (-5x)
b) (-2x5 – 4x3 + 3x2) : 2x2
Thực hiện phép chia đa thức sau bằng cách đặt tính chia:
a) (6x3 – 2x2 – 9x + 3) : (3x – 1)
b) (4x4 + 14x3 – 21x – 9) : (2x2 – 3)
Tìm số b sao cho đa thức x3 – 3x2 + 2x – b chia hết cho đa thức x – 3
Thực hiện các phép chia sau \(\frac{{9{x^2} + 5x + x}}{{3x}}\) và \(\frac{{(2{x^2} - 4x) + (x - 2)}}{{2 - x}}\)
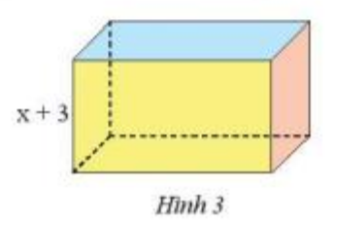
Tính diện tích đáy của một hình hộp chữ nhật (Hình 3) có chiều cao bằng (x + 3) cm và có thể tích bằng \(({x^3} + 8{x^2} + 19x + 12)\)\(c{m^3}\)
Thực hiện phép chia.
a) \((8{x^6} - 4{x^5} + 12{x^4} - 20{x^3}):4{x^3}\)
b) \((2{x^2} - 5x + 3):(2x - 3)\)
Tính chiều dài của một hình chữ nhật có diện tích bằng \((4{y^2} + 4y - 3)\)\(c{m^2}\) và chiều rộng bằng (2y – 1) cm.
Cho hình hộp chữ nhật có thể tích bằng (\(3{x^3} + 8{x^2} - 45x - 50\)) \(c{m^3}\), chiều dài bằng (x + 5) cm và chiều cao bằng (x + 1) cm. Hãy tính chiều rộng của hình hộp chữ nhật đó.
Thực hiện phép chia.
a) \((45{x^5} - 5{x^4} + 10{x^2}):5{x^2}\)
b) \((9{t^2} - 3{t^4} + 27{t^5}):3t\)
Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là \(A = ac,B = bc\). Biết \(MN = c\).
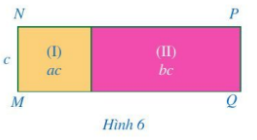
a) Tính NP.
b) So sánh: \((A + B):c\) và \(A:c + B:c\).
Cho đa thức \(P(x) = 4{x^2} + 3x\) và đơn thức \(Q(x) = 2x\).
a) Hãy chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x).
b) Hãy cộng các thương vừa tìm được.
Tính:
\((\dfrac{1}{2}{x^4} - \dfrac{1}{4}{x^3} + x):( - \dfrac{1}{8}x)\).
Tính:
a) \((4{x^3}):( - 2{x^2})\);
b) \(( - 7{x^2}):(6x)\);
c) \(( - 14{x^4}):( - 8{x^3})\).
Tính:
a) \((8{x^3} + 2{x^2} - 6x):(4x)\);
b) \((5{x^3} - 4x):( - 2x)\);
c) \(( - 15{x^6} - 24{x^3}):( - 3{x^2})\).
Tính:
a) \(({x^2} - 2x + 1):(x - 1)\);
b) \(({x^3} + 2{x^2} + x):({x^2} + x)\);
c) \(( - 16{x^4} + 1):( - 4{x^2} + 1)\);
d) \(( - 32{x^5} + 1):( - 2x + 1)\).
Một công ty sau khi tăng giá 30 nghìn đồng mỗi sản phẩm so với giá ban đầu là 2x (nghìn đồng) thì có doanh thu là \(6{x^2} + 170x + 1200\)(nghìn đồng). Tính số sản phẩm mà công ty đó đã bán được theo x.
Cho \(P(x) = {x^3} + {x^2} + x + 1\) và \(Q(x) = {x^4} - 1\). Tìm đa thức A(x) sao cho \(P(x).A(x) = Q(x)\).
Một công ty sau khi tăng giá 50 nghìn đồng mỗi sản phẩm so với giá ban đầu là x (nghìn đồng) với x < 60 thì có doanh thu là \( - 5{x^2} + 50x + 15000\)(nghìn đồng). Tính số sản phẩm mà công ty đã bán được theo x.
Đặt tính và làm phép chia sau:
\(a)\left( {{x^3} - 4{x^2} - x + 12} \right):\left( {x - 3} \right)\)
\(b)\left( {2{x^4} - 3{x^3} + 3{x^2} + 6x - 14} \right):\left( {{x^2} - 2} \right)\).
Khi làm phép chia \(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\), bạn Quỳnh cho kết quả đa thức dư là 4x + 2.
a) Không làm phép chia, hãy cho biết bạn Quỳnh đúng hay sai, tại sao?
b) Tìm thương và dư trong phép chia đó.
Cho đa thức \(A\left( x \right) = 3{x^4} + 11{x^3} - 5{x^2} - 19x + 10\). Tìm đa thức H(x) sao cho
\(A\left( x \right) = \left( {3{x^2} + 2x - 5} \right).H\left( x \right).\)
Tìm số m sao cho đa thức \(P\left( x \right) = 2{x^3} - 3{x^2} + x + m\) chia hết cho đa thức x + 2.
Cho đa thức \(P\left( x \right)\). Chứng minh rằng:
a) Nếu P(x) chia hết cho x – a thì a là một nghiệm của đa thức P(x);
b) Nếu x = a là một nghiệm của đa thức P(x) thì P(x) chia hết cho x – a.
Phép chia đa thức \(2{x^5} - 3{x^4} + {x^3} - 6{x^2}\) cho đa thức \(5{x^{7 - 2n}}\left( {n \in \mathbb{N};0 \le n \le 3} \right)\) là phép chia hết nếu:
A. n = 0
B. n = 1
C. n = 2
D. n = 3
Thực hiện phép chia.
a) \(\left( {64{y^2} - 16{y^4} + 8{y^5}} \right):4y\)
b) \(\left( {5{t^2} - 8t + 3} \right):\left( {t - 1} \right)\)
Thực hiện phép chia.
a) \(\left( {{x^4} + 6{x^2} + 8} \right):\left( {{x^2} + 2} \right)\)
b) \(\left( {3{x^3} - 2{x^2} + 3x - 2} \right):\left( {{x^2} + 1} \right)\)
Thực hiện phép chia \(\left( {2{x^2} - 5x + 3} \right):\left( {2x - 3} \right)\).







Danh sách bình luận