Trong không gian Oxyz, tính góc giữa đường thẳng \(d':\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = - 3 + 2t\;\\y = 1 + t\quad (t \in \mathbb{R})\;\\z = 2 + t\end{array}\end{array}} \right.\) và các mặt phẳng tọa độ: \((Oxy)\), \((Oxz)\), \((Oyz)\).
- Xác định vectơ chỉ phương \({\vec v_d} = (x',y',z')\) từ phương trình tham số của đường thẳng.
- Tùy vào mặt phẳng nào (Oxy, Oxz, Oyz), tìm vectơ pháp tuyến tương ứng của nó.
- Sử dụng công thức góc giữa đường thẳng và mặt phẳng:
\(\sin \theta = \frac{{|{{\vec v}_d} \cdot \vec n|}}{{|{{\vec v}_d}||\vec n|}}\)
với \({\vec v_d}\) là vectơ chỉ phương của đường thẳng, và \(\vec n\) là vectơ pháp tuyến của mặt phẳng.
Vectơ chỉ phương của đường thẳng \(d\) là \({\vec v_d} = (2,1,1)\).
Vectơ pháp tuyến của các mặt phẳng:
- Oxy: \({\vec n_{Oxy}} = (0,0,1)\)
- Oxz: \({\vec n_{Oxz}} = (0,1,0)\)
- Oyz: \({\vec n_{Oyz}} = (1,0,0)\)
Tính góc giữa đường thẳng \(d\) và các mặt phẳng:
- Với mặt phẳng Oxy:
\(\sin \theta = \frac{{|(2,1,1) \cdot (0,0,1)|}}{{\sqrt {{2^2} + {1^2} + {1^2}} \cdot \sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{|1|}}{{\sqrt 6 \cdot 1}} = \frac{1}{{\sqrt 6 }}\)
Do đó, góc \({\theta _{Oxy}} = \arcsin \left( {\frac{1}{{\sqrt 6 }}} \right)\).
- Với mặt phẳng Oxz:
\(\sin \theta = \frac{{|(2,1,1) \cdot (0,1,0)|}}{{\sqrt {{2^2} + {1^2} + {1^2}} \cdot \sqrt {{0^2} + {1^2} + {0^2}} }} = \frac{{|1|}}{{\sqrt 6 \cdot 1}} = \frac{1}{{\sqrt 6 }}\)
Do đó, góc \({\theta _{Oxy}} = \arcsin \left( {\frac{1}{{\sqrt 6 }}} \right)\).
- Với mặt phẳng Oyz:
\(\sin \theta = \frac{{|(2,1,1) \cdot (1,0,0)|}}{{\sqrt {{2^2} + {1^2} + {1^2}} \cdot \sqrt {{1^2} + {0^2} + {0^2}} }} = \frac{{|2|}}{{\sqrt 6 \cdot 1}} = \frac{2}{{\sqrt 6 }}\)
Do đó, góc \({\theta _{Oxy}} = \arcsin \left( {\frac{1}{{\sqrt 6 }}} \right)\).

Các bài tập cùng chuyên đề
Trong không gian Oxyz, tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P), với:
\(\Delta :\frac{{x + 2}}{{ - 1}} = \frac{{y - 4}}{2} = \frac{{z + 1}}{1},\left( P \right):x - y + z - 1 = 0\).
Trong không gian Oxyz, tính góc giữa trục Oz và mặt phẳng \(\left( P \right):x + 2y - z - 1 = 0\).
Tính góc giữa đường thẳng \(\Delta :\frac{{x + 1}}{{ - 1}} = \frac{{y - 3}}{2} = \frac{{z + 2}}{3}\) và mặt phẳng \(\left( P \right):x + y + z + 3 = 0\).
Trong không gian Oxyz, tính góc tạo bởi đường thẳng d: \(\frac{{x + 3}}{2} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 1}}{1}\) và mặt phẳng (P): \(x + y - 2z + 3 = 0\).
Bản thiết kế của một công trình được vẽ trong một hệ trục tọa độ Oxyz. Sàn nhà của công trình thuộc mặt phẳng Oxy, đường ống thoát nước thẳng và đi qua hai điểm \(A\left( {1;2; - 1} \right)\) và \(B\left( {5;6; - 2} \right)\). Tính góc tạo bởi đường ống thoát nước và mặt sàn.
Trong không gian Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l}x = 2 - t\\y = 3\\z = - 1 + 2t\end{array} \right.\) và mặt phẳng \(\left( P \right):2x - y - 2z + 1 = 0\). Cosin của góc giữa đường thẳng d và mặt phẳng (P) là
A. \(\frac{{2\sqrt 5 }}{5}\).
B. \(\frac{{\sqrt 5 }}{5}\).
C. \(\frac{{2\sqrt 3 }}{5}\).
D. \(\frac{{\sqrt 3 }}{5}\).
Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
a) \(\Delta :\left\{ \begin{array}{l}x = 1 + \sqrt 3 t\\y = 2\\z = 3 + t\end{array} \right.\) (t là tham số) và \(\left( P \right):\sqrt 3 x + z - 2 = 0\);
b) \(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 3 + t\end{array} \right.\) (t là tham số) và \(\left( P \right):x + y + z - 4 = 0\).
Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) (làm tròn kết quả đến hàng đơn vị của độ), biết \(\Delta :\left\{ \begin{array}{l}x = - 1 + 2t\\y = 4 - 3t\\z = - 1 + 4t\end{array} \right.\) (t là tham số) và \(\left( P \right):x + y + z + 3 = 0\).
Tính góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau:
a) \(d:\left\{ \begin{array}{l}x = 11 + 3t\\y = - 11 + t\\z = - 21 - 2t\end{array} \right.\) và \(\left( P \right):6x + 2y - 4z + 7 = 0.\)
b) \(d:\frac{{x - 3}}{2} = \frac{{y + 4}}{4} = \frac{{z - 5}}{2}\) và \(\left( P \right):2x + 2y - 4z + 1 = 0.\)
c) \(d:\frac{{x + 3}}{4} = \frac{{y + 5}}{4} = \frac{{z + 11}}{2}\) và \(\left( P \right):2y - 4z + 7 = 0.\)
Tính góc giữa đường thẳng \(d:\frac{{x + 2}}{2} = \frac{{y + 2}}{2} = \frac{{z - 1}}{1}\) và mặt phẳng \(\left( P \right):3y - 3z + 1 = 0\).
Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\) (làm tròn kết quả đến hàng đơn vị của độ), biết \(\Delta :\left\{ \begin{array}{l}x = - 1 - 5t\\y = 4 - 4t\\z = - 1 + 3t\end{array} \right.\) (với \(t\) là tham số) và \(\left( P \right):3{\rm{x}} + 4y + 5{\rm{z}} + 60 = 0\).
Trong không gian Oxyz, tính góc giữa đường thẳng:
\(\Delta :\frac{{x + 3}}{{ - 2}} = \frac{{y + 1}}{1} = \frac{{z - 1}}{2}\) và mặt phẳng \(\left( P \right):x + 2y - 2z + 3 = 0\)
Trong không gian Oxyz, góc giữa đường thẳng \(\Delta :\frac{{x + 3}}{1} = \frac{{y + 1}}{{\sqrt 2 }} = \frac{{z + 2}}{1}\) và mặt phẳng (Oxz) bằng
A. \({45^ \circ }\).
B. \({30^ \circ }\).
C. \({60^ \circ }\).
D. \({90^ \circ }\).
Trong không gian Oxyz, tại một phạm vi hẹp, (Oxy) là mặt phẳng nằm ngang. Một đường ống nước thẳng đi qua hai điểm \(A\left( {1;1;2} \right)\) và \(B\left( {1;2;1} \right)\). Hỏi đường ống nước trên nghiêng bao nhiêu độ (so với mặt phẳng nằm ngang)?
Cho đường thẳng d có vector chỉ phương \(\vec a\) và mặt phẳng \((\alpha )\) có vector pháp tuyến \(\vec n\). Gọi d' là hình chiếu của d trên \((\alpha )\). Gọi \(\phi \) là góc giữa d và \((\alpha )\), còn \(\phi '\) là góc giữa \(\vec a\) và \(\vec n\).

Tính góc giữa đường thẳng d và mặt phẳng \(\alpha \)
a) \(d:\frac{x}{1} = \frac{y}{2} = \frac{z}{2}\quad {\rm{và }}\quad \alpha :2x + 2y + 1 = 0\)
b) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 + 7t}\\{y = - 1 - 8t}\\{z = 1 - 15t}\end{array}} \right.,\quad (t \in \mathbb{R})\) và \(\alpha :2x + 2y + 1 = 0\)
c) \(d:\frac{x}{3} = \frac{y}{{ - 1}} = \frac{{z - 1}}{2},\quad \alpha :6x - 2y + 4z = 0\)
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x + 2y - 2z + 3 = 0\) và đường thẳng
\(d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{1}\). Tính góc tạo bởi đường thẳng \(d\) và mặt phẳng \(\left( P \right)\).
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(-3;-1;3) và N(-1;0;4) và mặt phẳng (P): x + 2y – z + 5 = 0. Tính góc giữa đường thẳng MN và mặt phẳng (P).
-
A.
\({30^o}\)
-
B.
\({45^o}\)
-
C.
\({60^o}\)
-
D.
\({90^o}\)
Trong không gian với hệ trục tọa độ Oxyz, tính sin góc giữa đường thẳng d: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 1 + 3t\\z = 2 - t\end{array} \right.\) và mặt phẳng (P): 2x – y + 2z – 1 =0.
-
A.
\(\frac{{\sqrt {14} }}{{42}}\)
-
B.
\(\frac{{\sqrt {14} }}{{22}}\)
-
C.
\(\frac{{\sqrt 7 }}{{42}}\)
-
D.
Đáp án khác
Trong không gian với hệ trục tọa độ Oxyz, (Oxy) là mặt đất, một máy bay cất cánh với vận tốc \(\overrightarrow v = (150;150;40)\). Tính góc nâng của của máy bay (góc giữa hướng chuyến động bay lên của máy bay với đường băng) và làm tròn kết quả đến hàng đơn vị.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: \(\frac{{x - 3}}{2} = \frac{{y - 2}}{1} = \frac{z}{1}\) và mặt phẳng (P): \(3x + 4y + 5z + 8 = 0\). Góc hợp giữa đường thẳng d và mặt phẳng (P) bằng bao nhiêu độ?
Trong không gian Oxyz, mặt phẳng (Oyz) là mặt phẳng nằm ngang. Một đường ống nước thẳng đi qua hai điểm A(-1;1;2), B(2;1;3). Hỏi đường ống nước nói trên nghiêng bao nhiêu độ so với mặt phẳng nằm ngang (kết quả làm tròn đến độ)?
Khi gắn hệ tọa độ Oxyz (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng (Oxy) trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí A(3;-2;3) đến vị trí B(8;8;0). Góc giữa đường bay (một phần của đường thẳng AB và sân bay (một phần của mặt phẳng (Oxy)) bằng \(\alpha \) độ. Khi đó, giá trị của bằng \(\alpha \) bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
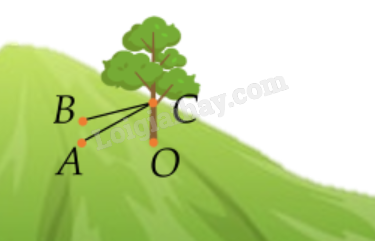
Trên một sườn núi (có độ nghiêng đều), người ta trồng một cây thông và muốn giữ nó không bị nghiêng bằng hai sợi dây neo như hình vẽ. Giả thiết cây thông mọc thẳng đứng và trong một hệ tọa độ phù hợp, các điểm O (gốc cây thông), A, B (nơi buộc dây neo) có tọa độ tương ứng là O(0;0;0), A(3;-2;1), B(-5;-3;1) (đơn vị trên mỗi trục tọa độ là mét). Biết rằng hai sợi dây neo đều được buộc vào thân cây tại điểm C(0;0;5) và dây kéo căng tạo thành các đoạn thẳng. Tổng các góc tạo bởi mỗi dây neo và mặt phẳng sườn núi bằng bao nhiêu độ (làm tròn số đo các góc đến hàng đơn vị của độ).







Danh sách bình luận