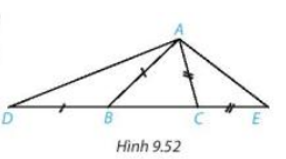
Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
a) \(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)
-Chứng minh .
-\(\widehat {ABD} = {180^0} - 2\widehat {ADB}\),\(\widehat {ACE} = {180^0} - 2\widehat {AEC}\)
b)Sử dụng kết quả câu a)
a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).

Các bài tập cùng chuyên đề
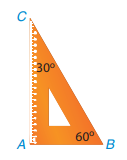
Quan sát ê ke có góc 60\(^\circ \) (H.9.2). Kí hiệu đỉnh góc vuông là A, đỉnh góc 60\(^\circ \) là B và đỉnh góc 30\(^\circ \) là C.
·Sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn. Sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn.
·Góc lớn nhất đối diện với cạnh nào? Góc bé nhất đối diện với cạnh nào?
Em hãy vẽ một tam giác ABC có AB = 3 cm, AC = 5 cm. Quan sát hình vừa vẽ và dự đoán xem trong hai góc B và C, góc nào lớn hơn.
Cho tam giác MNP có độ dài các cạnh MN = 3 cm, NP = 5 cm, MP = 7 cm. Hãy xác định góc đối diện với từng cạnh rồi sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn.
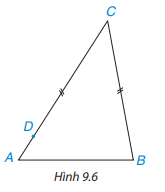
Trong Hình 9.6 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao?
\(\begin{array}{l}a)\widehat A = \widehat B\\b)\widehat A > \widehat B\\c)\widehat A < \widehat B\end{array}\)
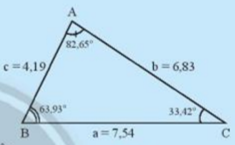
Cho tam giác ABC trong Hình 1.
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a,b,c
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc A,B,C là các góc đối diện với ba cạnh a,b,c.
- Nêu nhận xét của em về hai kết quả sắp xếp trên.
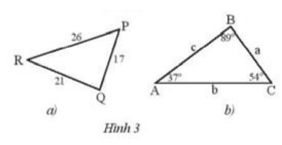
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR trong Hình 3a.
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC trong Hình 3b.
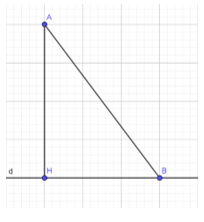
Quan sát tam giác AHB ở Hình 6.
a) Hãy cho biết trong hai góc AHB và ABH, góc nào lớn hơn
b) Từ câu a, hãy giải thích vì sao AB > AH.
a) So sánh các góc của tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 6 cm.
b) So sánh các cạnh của tam giác ABC có \(\widehat A\)\( = {50^o}\),\(\widehat C\)\( = {50^o}\)
Quan sát tam giác ABC ở Hình 17.
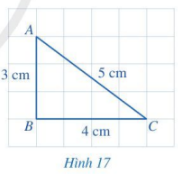
a) So sánh hai cạnh AB và AC.
b) So sánh góc B (đối diện với cạnh AC) và góc C (đối diện với cạnh AB).
Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
Quan sát tam giác ABC ở Hình 19.
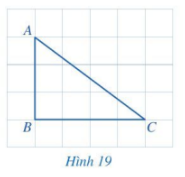
a) So sánh hai góc B và C.
b) So sánh cạnh AB (đối diện với góc C) và cạnh AC (đối diện với góc B).
a) Cho tam giác DEG có góc E là góc tù. So sánh DE và DG.
b) Cho tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Tìm cạnh nhỏ nhất, cạnh lớn nhất của tam giác MNP.
Cho tam giác MNP có \(MN = 6\)cm, \(NP = 8\)cm, \(PM = 7\)cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
Cho tam giác MNP có \(\widehat M = 80^\circ \) và \(\widehat N = 50^\circ \). So sánh độ dài NP và MP là
-
A.
NP > MP;
-
B.
NP = MP;
-
C.
NP < MP;
-
D.
Không đủ điều kiện để so sánh.
Cho tam giác ABC có AB < AC, AD là tia phân giác của \(\widehat {BAD}\) (D ∈ BC). Chứng minh \(\widehat {ADB} < \widehat {ADC}\) .
Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng 600.
Cho tam giác ABC có AB > AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.
a) Hãy so sánh các góc \(\widehat {AMB}\) và \(\widehat {ANC}\).
b) Hãy so sánh các đoạn AM và AN.
Cho tam giác ABC có \(AB = 2cm,BC = 4cm,CA = 4,5cm\). Khi đó:
A. \(\widehat B < \widehat A\).
B. \(\widehat A < \widehat B < \widehat C\).
C. \(\widehat A < \widehat C < \widehat B\).
D. \(\widehat C < \widehat A < \widehat B\).
Trong Hình 9.1 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao?
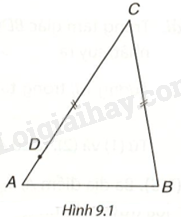
a) \(\widehat A = \widehat B\).
b) \(\widehat A > \widehat B\).
c) \(\widehat A < \widehat B\).
Cho tam giác ABC có \(\widehat A:\widehat B:\widehat C = 5:4:6\). Tính các góc của tam giác ABC, từ đó hãy so sánh độ dài ba cạnh của tam giác ABC.
Cho ΔABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng?
-
A.
\(\widehat A > \widehat B > \widehat C\)
-
B.
\(\widehat C > \widehat A > \widehat B\)
-
C.
\(\widehat C < \widehat A < \widehat B\)
-
D.
\(\widehat A < \widehat B < \widehat C\)
Cho \(\Delta ABC\) có \(AC > BC > AB\). Trong các khẳng định sau, câu nào đúng?
-
A.
\(\widehat A > \widehat B > \widehat C\)
-
B.
\(\widehat C > \widehat A > \widehat B\)
-
C.
\(\widehat C < \widehat A < \widehat B\)
-
D.
\(\widehat A < \widehat B < \widehat C\)
A. \(\angle B < \angle C < \angle A\)
B. \(\angle C < \angle A < \angle B\)
C. \(\angle A > \angle B > \angle C\)
D. \(\angle C < \angle B < \angle A\)
A.\(\angle B < \angle C < \angle A\).
B.\(\angle C < \angle A < \angle B\).
C.\(\angle A > \angle B > \angle C\).
D.\(\angle C < \angle B < \angle A\).
A. \(\angle B < \angle C < \angle A\)
B. \(\angle C < \angle A < \angle B\)
C. \(\angle A > \angle B > \angle C\)
D. \(\angle C < \angle B < \angle A\)
Cho các góc sau \(\widehat A = 30^\circ ;\,\widehat B = 60^\circ ;\,\widehat C = 110^\circ ;\widehat D = 90^\circ \). Chọn câu sai.
-
A.
\(\widehat B < \widehat D\)
-
B.
\(\widehat C < \widehat D\)
-
C.
\(\widehat A < \widehat B\)
-
D.
\(\widehat B < \widehat C\)
Tam giác ABC có AB = 8cm, BC = 6cm, AC = 4cm. So sánh các góc của tam giác ta có:
-
A.
\(\widehat A < \widehat B < \widehat C\).
-
B.
\(\widehat A < \widehat C < \widehat B\).
-
C.
\(\widehat B < \widehat A < \widehat C\).
-
D.
\(\widehat C < \widehat B < \widehat A\).
A. \(\widehat A > \widehat B > \widehat C\).
B. \(\widehat C > \widehat A > \widehat B\).
C. \(\widehat A < \widehat B < \widehat C\).
D. \(\widehat C < \widehat A < \widehat B\).
Cho các góc sau \(\widehat A = {100^o};\,\widehat B = {80^o};\,\widehat C = {180^o};\widehat D = {30^o}\). Chọn câu sai.
-
A.
\(\widehat D < \widehat B\)
-
B.
\(\widehat D < \widehat C\)
-
C.
\(\widehat B < \widehat A\)
-
D.
\(\widehat C < \widehat B\)







Danh sách bình luận