Trong Hình 54, độ rộng của khúc sông được tính bằng khoảng cách giữa hai vị trí C, D. Giả sử chọn được các vị trí A, B, E sao cho \(\Delta ABE \backsim \Delta ACD\) và đo được \(AB = 20m,\,\,AC = 50m,\,\,BE = 8m\). Tính độ rộng của khúc sông đó.
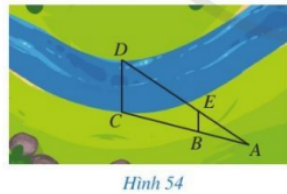
Dựa vào hệ số đồng dạng để tính độ dài cạnh CD trong tam giác ACD.
Vì \(\Delta ABE \backsim \Delta ACD\) nên ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Leftrightarrow \frac{{20}}{{50}} = \frac{8}{{CD}} \Rightarrow CD = 8.50:20 = 20\)
Vậy độ rộng của khúc sông là 20m.

Các bài tập cùng chuyên đề
Cho \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\) và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
-
A.
\({C_{\Delta MNI}} = 30m,{C_{\Delta ABC}} = 46m.\)
-
B.
\({C_{\Delta MNI}} = 56m,{C_{\Delta ABC}} = 40m.\)
-
C.
\({C_{\Delta MNI}} = 24m,{C_{\Delta ABC}} = 40m.\)
-
D.
\({C_{\Delta MNI}} = 40m,{C_{\Delta ABC}} = 56m.\)
Để đo khoảng cách giữa hai địa điểm \({\rm{D}}\), \({\rm{E}}\) ở hai bên bờ của một con sông, người ta chọn các vị trí \({\rm{A}}, {\rm{B}}, {\rm{C}}\) ở cùng một bên bờ với điểm \(D\) và đo được \(AB = 2{\rm{\;m}},AC = 3{\rm{\;m}},CD = 15{\rm{\;m}}\). Giả sử $\Delta ABC\backsim \Delta DEC$. Tính khoảng cách \(DE\).
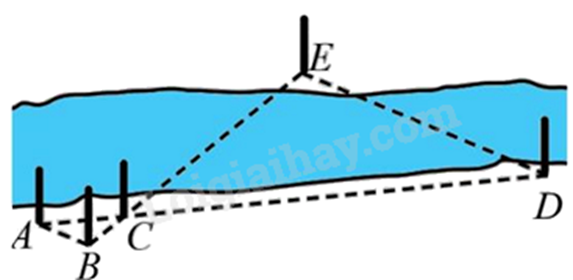
-
A.
\(10{\rm{\;m}}\)
-
B.
\(12{\rm{\;m}}\)
-
C.
\(9{\rm{\;m}}\)
-
D.
\(15{\rm{\;m}}\)
Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B). Theo em bác Dương đã tính như thế nào để ra được chiều cao cột đèn?
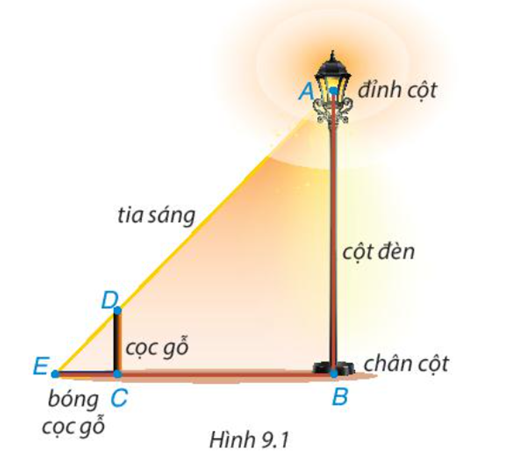
Trong hình 9.2, ΔABC và ΔDEF là hai tam giác có các cạnh tương ứng song song và các góc tương ứng bằng nhau, tức là AB // DE, AC // DF, BC // EF và \(\widehat A = \widehat D{,^{}}\widehat B = \widehat E{;^{}}\widehat C = \widehat F\)

Nhìn hình vẽ, hãy cho biết giá trị các tỉ số sau: \(\frac{{AB}}{{DE}}{;^{}}\frac{{BC}}{{EF}}{;^{}}\frac{{AC}}{{DF}}\)
Trong các tam giác được vẽ trên ô lưới vuông, có một cặp tam giác đồng dạng. Hãy chỉ ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng.

Cho \(\Delta ABC \backsim \Delta MNP\). Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì tam giác MNP cân tại đỉnh M.
b) Nếu tam giác ABC đều thì tam giác MNP đều.
c) Nếu \(AB \ge AC \ge BC\) thì \(MN \ge MP \ge NP\)
Cho ΔABC \(\backsim\) ΔMNP, khẳng định nào sau đây không đúng?
a) ΔMNP \(\backsim\) ΔABC
b) ΔBCA \(\backsim\) ΔNPM
c) ΔCAB \(\backsim\) ΔPNM
d) ΔACB \(\backsim\) ΔMNP
Khẳng định nào sau đây là đúng?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác bất kì đồng dạng với nhau
c) Hai tam giác đều bất kì đồng dạng với nhau
d) Hai tam giác vuông bất kì đồng dạng với nhau
e) Hai tam giác đồng dạng thì bằng nhau
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng \(\widehat {BAC} = \widehat {PMN}\), AB=2MN. Chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng
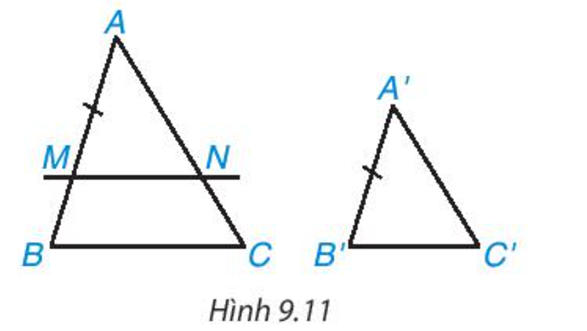
Cho hai tam giác ABC và A'B'C' có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
a) Nếu A′B=AB thì hai tam giác có đồng dạng với nhau không? Vì sao?
b) Nếu A′B < AB như hình 9.11. Trên đoạn thẳng AB lấy điểm M sao cho AM = A'B'. Kẻ đường thẳng qua M song song với BC và cắt AC tại N.
- Hãy giải thích vì sao ΔAMN ∽ ΔABC
- Hãy chứng tỏ rằng AN=A’C’′, MN=B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c)
- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?
Nếu ΔABC ∽ ΔA′B′C′ và anh Pi đo được A′C′=3,76cm thì khoảng cách từ bạn Tròn đến chân cột cờ là bao nhiêu mét?
Cho ΔABC ∽ ΔDEF. Biết \(\widehat A = {60^o};\widehat E = {80^o}\), hãy tính số đo các góc \(\widehat B,\widehat C,\widehat D,\widehat F\)
Cho ΔABC ∽ ΔA'B'C'. Biết AB=3cm, A′B′=6cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'
Cho ABC là tam giác không cân. Biết ΔA′B′C′ ∽ ΔABC. Khẳng định nào sau đây là đúng?
A. ΔA′C′B′ ∽ ΔACB
B. ΔB′C′A′ ∽ ΔBAC
C. ΔB′A′C′ ∽ ΔBCA
D. ΔA′C′B′ ∽ ΔABC
Cho ΔA′B′C′ ∽ ΔABC với tỉ số đồng dạng bằng 2. Khẳng định nào sau đây là đúng:
A. \(\frac{{AB}}{{A'B'}} = 2\)
B. \(\frac{{AB}}{{A'C'}} = 2\)
C. \(\frac{{A'B'}}{{AB}} = 2\)
D. \(\frac{{A'B'}}{{AC}} = 2\)
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều nào dưới đây không suy ra ΔABC ∽ ΔDEF
A. \(\widehat B = \widehat E\)
B. \(\widehat C = \widehat F\)
C. \(\widehat B + \widehat C = \widehat E + \widehat F\)
D. \(\widehat B - \widehat C = \widehat E - \widehat F\)
Hai tam giác có ba cạnh bằng nhau thì bằng nhau. Còn hai tam giác có ba góc bằng nhau thì có bằng nhau không?
Nêu nhận xét về hình dạng và kích thước của từng cặp hình: Hình 1a và Hình 1b, Hình 1c và Hình 1d, Hình 1e và Hình 1g.

Cho tam giác \(ABC\) và tam giác \(A'B'C'\) như Hình 2.
a) Hãy viết các cặp góc bằng nhau.
b) Tính và so sánh các tỉ số
\(\frac{{A'B'}}{{AB}};\frac{{A'C'}}{{AC}};\frac{{B'C'}}{{BC}}\).

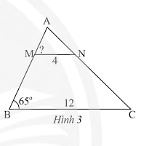
Quan sát Hình 3, cho biết \(\Delta AMN\backsim\Delta ABC\).
a) Hãy viết tỉ số của các cạnh tương ứng và tính tỉ số đồng dạng.
b) Tính góc \(\widehat {AMN}\).
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) có đồng dạng với tam giác \(ABC\) không? Tỉ số đồng dạng là bao nhiêu?
b) Cho tam giác \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng \(k\) thì \(\Delta ABC\backsim\Delta A'B'C'\) theo tỉ số nào?
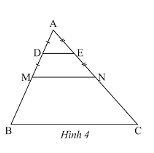
Quan sát Hình 4, cho biết \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,DE\) là đường trung bình của tam giác \(AMN,MN\) là đường trung bình của tam giác \(ABC.\) Tam giác \(ADE\) đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng là bao nhiêu?
Quan sát Hình 5, biết \(MN//BC\). Hãy điển ? cho thích hợp.
\(\Delta AMN\) và\(\Delta ABC\) có:
\(\widehat A\) chung;
\(\widehat M = ?\);
\(\widehat N = ?\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{?}{?}\)
Nêu nhận xét về mối quan hệ giữa tam giác \(AMN\) và tam giác \(ABC\).

Quan sát Hình 8, cho biết \(DC//MP,EF//MQ\).
a) Chứng minh rằng \(\Delta EPF\backsim\Delta DCQ\).
b) \(\Delta ICF\) có đồng dạng với \(\Delta MPQ\)không? Tại sao?

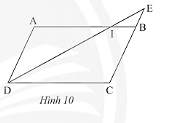
Trong Hình 10, cho biết \(ABCD\) là hình bình hành.
a) Chứng minh rằng \(\Delta IEB\backsim\Delta IDA\).
b) Cho biết \(CB = 3BE\) và \(AI = 9cm\). Tính \(DC\).
Trong hai khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Tại sao?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác đồng với với nhau thì bằng nhau.
Cho tam giác \(ABC\), hãy vẽ một tam giác đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng \(k = \frac{1}{2}\).
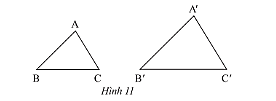
a) Trong Hình 11, cho biết \(\Delta ABC\backsim\Delta A'B'C'\). Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.
b) Trong Hình 12, cho biết \(\Delta DEF\backsim\Delta D'E'F'\). Tính số đo \(\widehat {D'}\) và \(\widehat F\).

c) Trong Hình 12, cho biết \(\Delta MNP\backsim\Delta M'N'P'\). Tính độ dài các đoạn thẳng \(MN\) và \(MP'\).

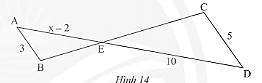
Trong Hình 14, cho biết \(AB//CD\)
a) Chứng minh rằng \(\Delta AEB\backsim\Delta DEC\).
b) Tìm \(x\).
Cho \(\Delta ABC\backsim\Delta DEF\) theo tỉ sống đồng dạng \(k = \frac{2}{5}\).
a) Tính tỉ số chu vi của hai tam giác đã cho.
b) Cho biết hiệu chu vi hai tam giác trên là 36cm, tính chu vi mỗi tam giác.







Danh sách bình luận