Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho \(AP = PN = NB\). Gọi Q là giao điểm của AM và CP. Chứng minh:
a) \(MN//CP\)
b) \(AQ = QM\)
c) \(CP = 4PQ\)
a) Chứng minh MN là đường trung bình của tam giác BPC.
b) Sử dụng định lý Thales trong tam giác AMN để chứng minh.
c) Sử dụng định lý đường trung bình để chứng minh.
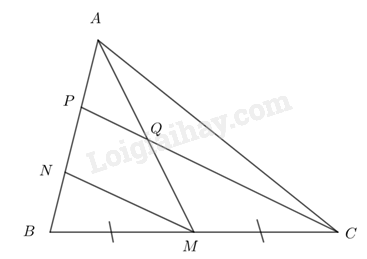
a) Vì \(AP = PN = NB\) nên N là trung điểm BP.
Mà M là trung điểm BC nên MN là đường trung bình của tam giác BPC.
\( \Rightarrow MN//CP\)
b) Tam giác AMN có \(MN//CP\) nên:
\(\frac{{AP}}{{PN}} = \frac{{AQ}}{{QM}}\) (Định lý Thales)
Mà \(AP = PN = NB\) nên P là trung điểm AN hay \(\frac{{AP}}{{PN}} = 1\)
\( \Rightarrow \frac{{AQ}}{{QM}} = 1 \Rightarrow AQ = QM\).
c) P là trung điểm AN, Q là trung điểm AM nên PQ là đường trung bình của tam giác AMN.
\( \Rightarrow PQ = \frac{1}{2}MN\)
Mà MN là đường trung bình của tam giác BPC nên \(MN = \frac{1}{2}CP \Rightarrow CP = 2MN\)
Vậy \(CP = 4PQ\).
Các bài tập cùng chuyên đề
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang.
b) Tứ giác MNPB là hình gì? Tại sao?
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK // CD, FK // AB.
b) So sánh EF và \(\dfrac{1}{2}(AB + C{\rm{D}})\)
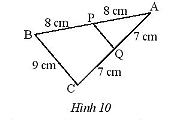
Tính độ dài đoạn \(PQ\) (Hình 10).
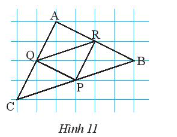
Cho biết cạnh mỗi ô vuông bằng \(1cm\). Tính độ dài các đoạn \(PQ,PR,RQ,AB,BC,CA\) trong Hình 11.
Cho tam giác \(ABC\) nhọn. Gọi \(M,N,P\) lần lượt là trung điểm của \(AB;AC;BC\). Kẻ đường cao \(AH\). Chứng minh rằng tứ giác \(MNPH\) là hình thang cân.
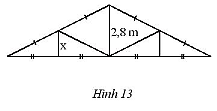
Một mái nhà được vẽ như Hình 13. Tính độ dài \(x\) trong hình mái nhà.
Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh \(DE\), cho biết \(BC = 232m\) và \(B,C\) lần lượt là trung điểm của \(AD\) và \(AE\).
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh tứ giác MNPQ là hình bình hành.
b) Cho \(AC = BD\). Chứng minh tứ giác MNPQ là hình thoi.
c) Cho \(AC \bot BD\). Chứng minh tứ giác MNPQ là hình chữ nhật.
Cho tam giác \(ABC\), các đường trung tuyến \(BD, CE\). Gọi \(M, N\) theo thứ tự là trung điểm của \(BE, CD\). Gọi \(I, K\) theo thứ tự là giao điểm của \(MN\) với \(BD\) và \(CE\) Chứng minh rằng:
a) \(\)\(\)\(ED\parallel BC\)
b) \(\)\(\)\(MN\parallel BC\)
c) \(MI = IK = KN\).
Cho \(\Delta ABC\), trung tuyến \(AM\), đường phân giác của \(\widehat {AMB}\) cắt \(AB\) ở \(D\) đường phân giác của \(\widehat {AMC}\) cắt \(AC\) ở \(E\).
a) Chứng minh rằng \(AD.AC = AE.AB\) và \(DE\parallel BC\).
b) Gọi \(I\) là giao điểm của \(AM\) và \(DE\). Chứng minh rằng \(I\) là trung điểm của \(DE\).
c) Tính \(DE\), biết \(BC = 30\,cm\) và \(AM = 10\,cm\).
d) Tam giác \(ABC\) phải thêm điều kiện gì để \(DE\) là đường trung bình của tam giác đó?
Giữa hai điểm A, B là một hồ nước sâu. Biết A, B lần lượt là trung điểm của MC, MD (xem hình vẽ).
Bạn Mai đi từ C đến D với vận tốc 9,6km/h hết 1 phút 30 giây. Hỏi hai điểm A và B cách nhau bao nhiêu mét?
Cho tam giác nhọn ABC có M, N lần lượt là trung điểm của AB, AC.
a) Chứng minh tứ giác BMNC là hình thang.
b) Gọi E là trung điểm của BC và I là giao điểm của AE với MN. Chứng minh I là trung điểm của MN.
Cho tam giác nhọn ABC, kẻ trung tuyến AM \(\left( {M \in BC} \right)\). Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh:
a) \(EF = FB\);
b) \(AE = \frac{1}{3}AB\);
c) \(CE = 4EI\).
Cho tam giác ABC, hai đường trung tuyến BM và CN cắt nhau tại G \(\left( {M \in AC,N \in AB} \right)\). Gọi D, E lần lượt là trung điểm của GB, GC. Chứng minh:
a) MN//DE
b) ND//ME
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM//QO\(\left( {M \in OP} \right)\), IN//PO \(\left( {N \in QO} \right)\). Chứng minh:
a) Tam giác IMN cân tại I.
b) OI là đường trung trực của MN.
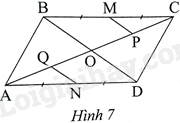
Cho hình bình hành ABCD có M, N lần lượt là trung điểm của BC, AD. Vẽ MP//BD \(\left( {P \in AC} \right)\) và \(NQ//BD\left( {Q \in AC} \right)\). Phát biểu nào sau đây đúng?
A. \(AQ = QP = PC\).
B. O là trung điểm PQ.
C. MNPQ là hình bình hành.
D. MNPQ là hình chữ nhật.
Chọn phát biểu đúng trong các phát biểu sau:
a) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng một phần ba cạnh đó.
b) Trong một tam giác chỉ có một đường trung bình.
c) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh tam giác đó.
d) Đường trung bình của tam giác là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện.
Cho tam giác \(ABC\) cân tại \(A\), có \(M\) là trung điểm của \(BC\). Kể tia \(Mx\) song song với \(AC\) cắt \(AB\) tại \(E\) và tia \(My\) song song với \(AB\) cắt \(AC\) tại \(F\). Chứng minh:
a) \(EF\) là đường trung bình của tam giác \(ABC\);
b) \(AM\) là đường trung trực của \(EF\).
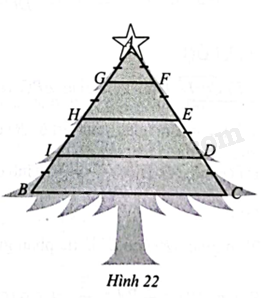
Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân \(ABC\)
(\(AB = AC = 2\) m) cùng các thanh sắt nằm ngang \(GF,HE < ID,BC\) và sau đó gắn cây thông như Hình 22. Tính số tiền sắt cần sử dụng để làm cây thông noel đó.
Biết giá một mét sắt là 55 000 đồng và \(AG = GH = HI = IB,CD = DE = EF = FA\), thanh \(GF\) dài \(0,2\) m.
Cho hình chữ nhật \(ABCD\). Kẻ \(CH\) vuông góc với \(BD\left( {H \in BD} \right)\). Gọi \(I,K,M\) lần lượt là trung điểm của \(BH,CH,AD\). Chứng minh:
a) Tứ giác \(IKDM\) là hình bình hành;
b) Gọi \(N\) là giao điểm của \(IM\) và \(AH\). Hỏi \(IN\) có thể là đường trung bình của tam giác \(HAB\) không? Vì sao?
Cho tứ giác \(ABCD\) có \(AD = BC\). Đường thẳng đi qua trung điểm \(M\) và \(N\) lần lượt của các cạnh \(AB\) và \(CD\) cắt các đường thẳng \(AD\) và \(BC\) lần lượt tại \(E\) và \(F\). Chứng minh: \(\widehat {AEM} = \widehat {MFB}\).
Cho tứ giác \(ABCD\) có \(M,N\) lần lượt là trung điểm của \(AD,BC\). Chứng minh: \(MN \le \frac{{AB + DC}}{2}\). Dấu đẳng thức xảy ra khi nào?
