Cho hàm số \(y = f(x) = {x^3} - 3{x^2} + 3\)
a) Sử dụng phần mềm GeoGebra vẽ đồ thị (C) của hàm số đã cho.
b) Tìm nghiệm gần đúng (làm tròn đến hàng phần trăm) của phương trình \(f(x) = 0\)
c) Dựa vào đồ thị đã vẽ ở câu a, biện luận theo tham số m số nghiệm của phương trình \({x^3} - 3{x^2} + 3 = m\).
a) Mở GeoGebra và nhập hàm số f(x).
b) Sử dụng câu lệnh Nghiem( Đa thức ) để tìm các nghiệm gần đúng.
c)
- Tạo thanh trượt m và vẽ hàm số y = m
- Quan sát và biện luận
a)
- Mở GeoGebra và nhập hàm số \(f(x) = {x^3} - 3{x^2} + 3\)
- Đồ thị của hàm số sẽ trông như sau:
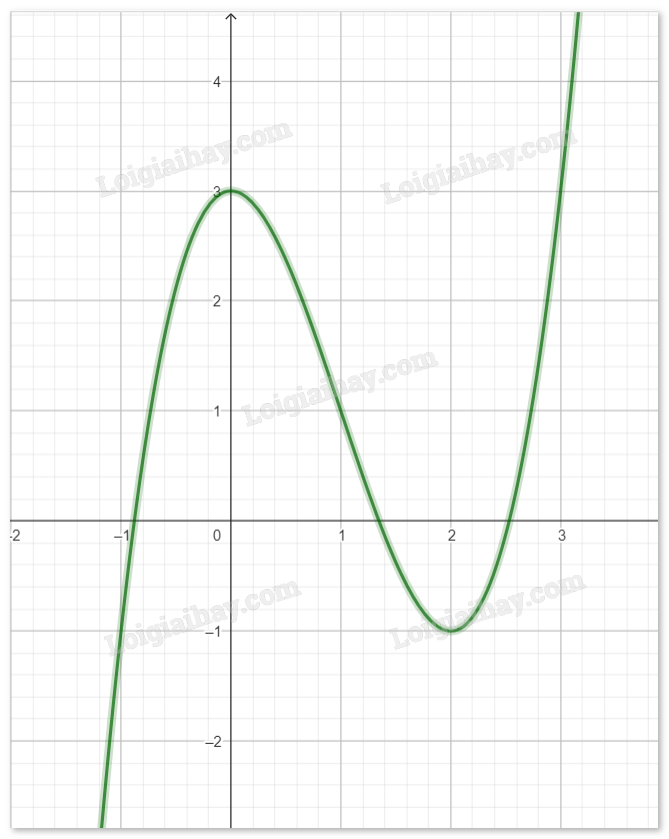
b) Sử dụng câu lệnh Nghiem(Đa thức) để tìm các điểm mà đồ thị cắt trục x sẽ ra được kết quả như sau:

Từ đó, ta thấy phương trình \(f(x) = 0\) có các nghiệm là: \({x_1} \approx - 0.88,{x_2} \approx 1.35,{x_3} \approx 2.53\)
c)
- Tạo thanh trượt m với m nằm trong khoảng (-5,5)
- Vẽ đồ thị hàm số y = m
- Số giao điểm của hai đồ thị sẽ là nghiệm của phương trình \({x^3} - 3{x^2} + 3 = m\)(*)
- Kéo thanh trượt m ta sẽ thấy sự thay đổi của các nghiệm
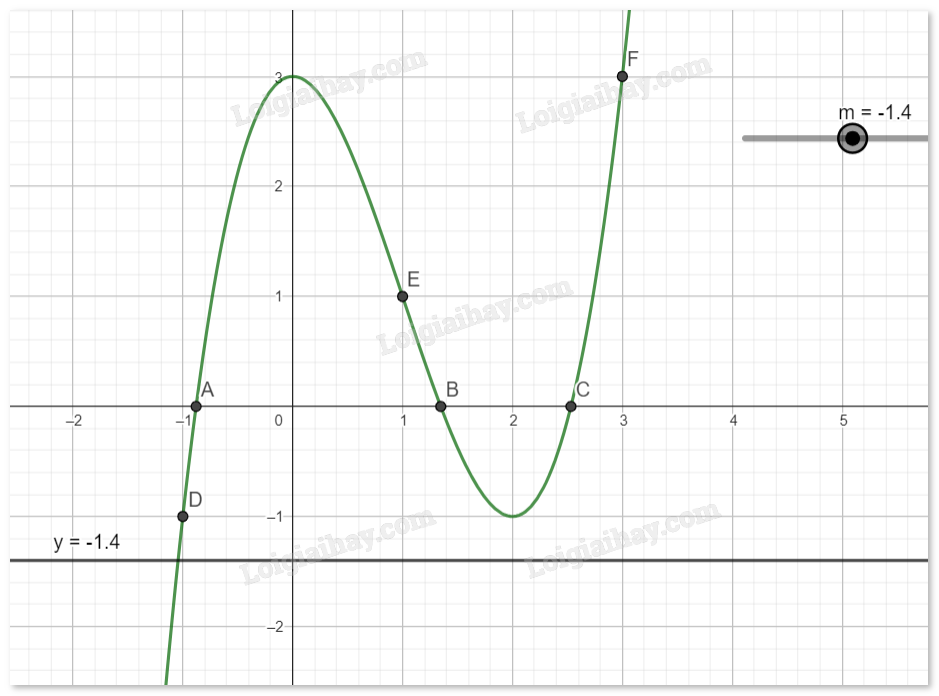
Với \(m > 3\), phương trình (*) có 1 nghiệm.
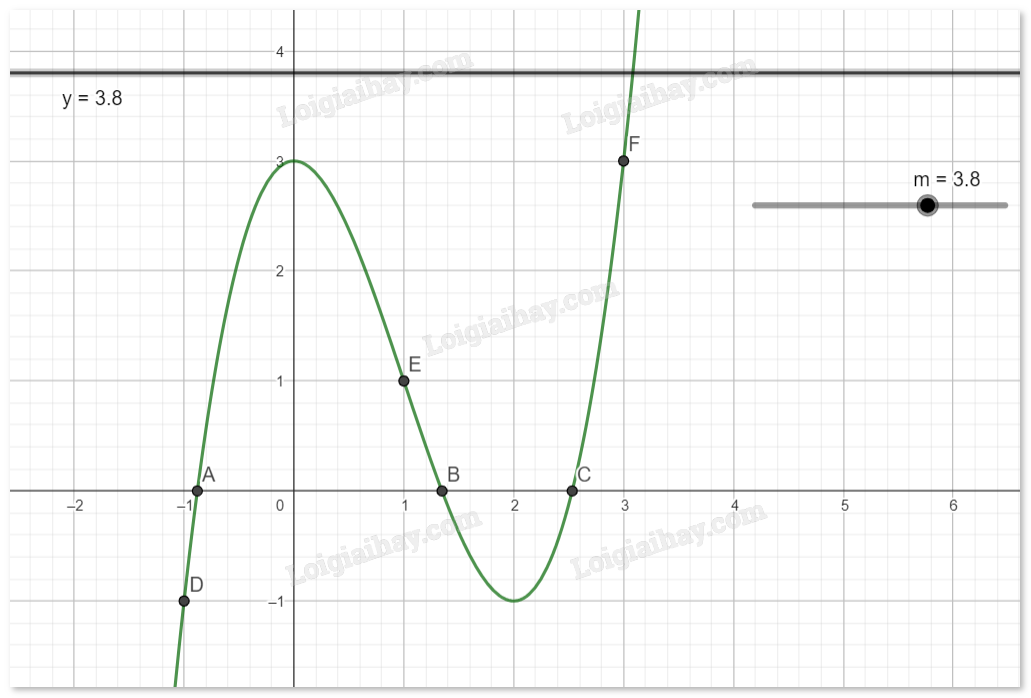
Với \(m = 3\), phương trình (*) có 2 nghiệm.
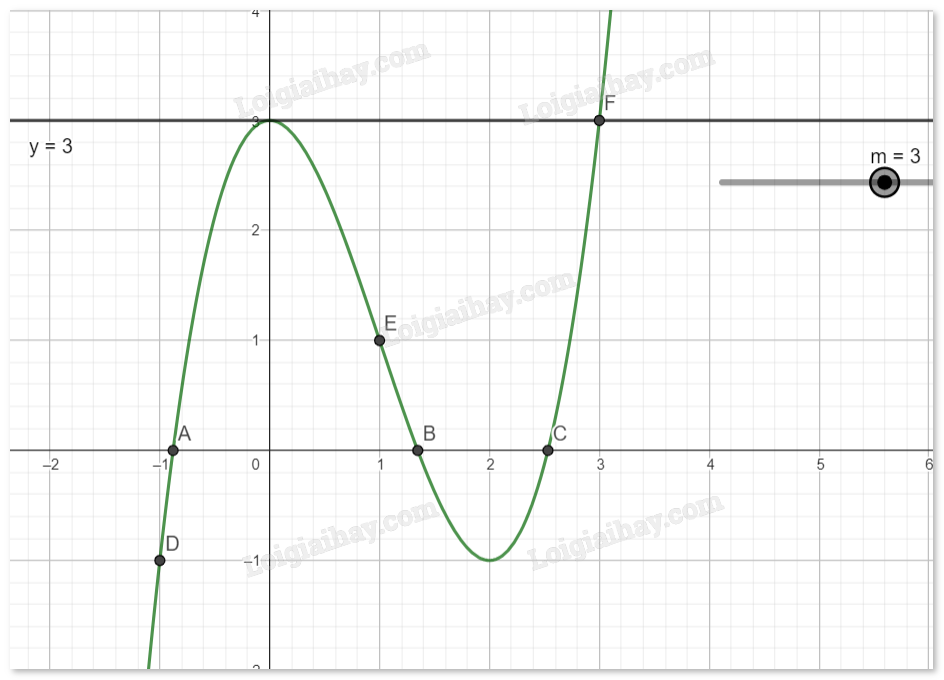
Với \( - 1 < m < 3\), phương trình (*) có 3 nghiệm phân biệt.
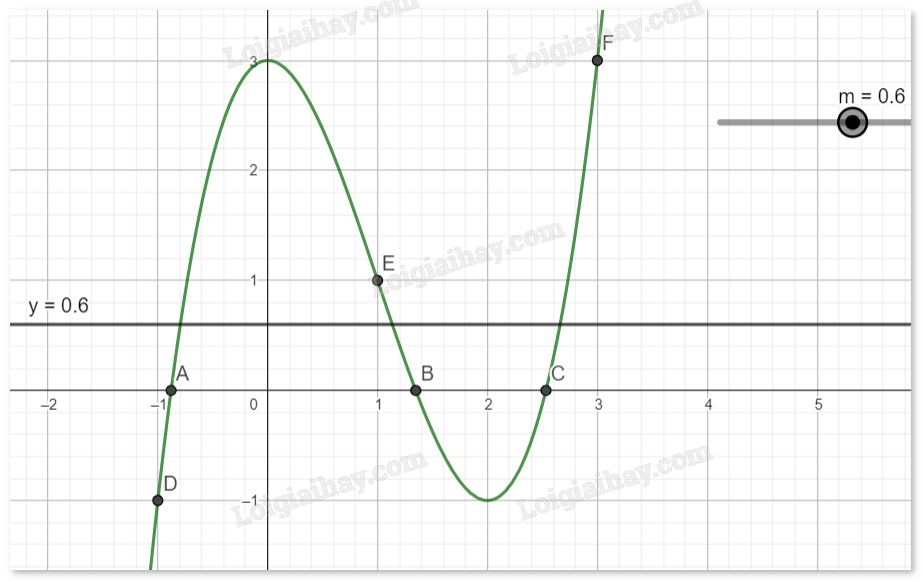
Với \(m = - 1\), phương trình (*) có 2 nghiệm.
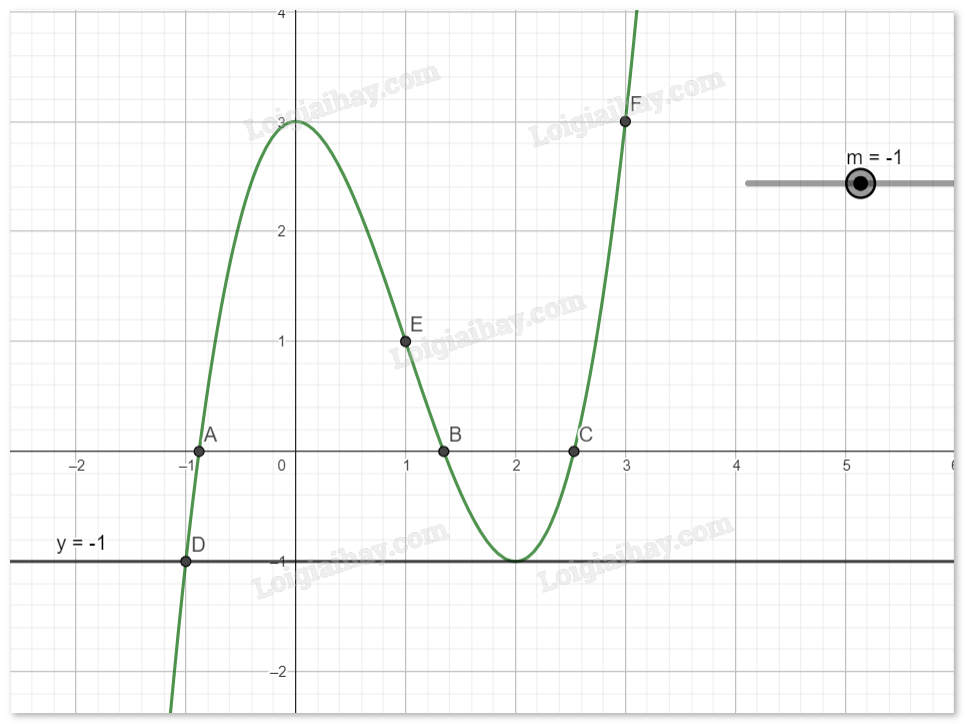
Với \(m < - 1\), phương trình (*) có 1 nghiệm.

Các bài tập cùng chuyên đề
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Cho các hàm số đa thức sau:
(1) \(y = 3{x^2} + \sqrt 3 x + 1\); (2) \(y = {x^3} - 6{x^2} + 9\), (3) \(y = {x^4} - 4{x^2} + 3\).
a) Tìm đạo hàm cấp một và đạo hàm cấp hai của các hàm số trên.
b) Tìm tất cả các điểm cực trị của các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Cho các hàm số phân thức hữu tỉ sau:
(1) \(y = \frac{x}{{x + \sqrt 2 }}\); (2) \(y = \frac{{2x - 1}}{{x + 1}}\); (3) \(y = \frac{{{x^2} - 2x - 8}}{{x - 1}}\); \(y = 5x + 1 + \frac{3}{{2x - 3}}\).
a) Tìm đạo hàm cấp một của các hàm số trên.
b) Tìm các đường tiệm cận của đồ thị các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\).
b) \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\).
c) \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\).
d) \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
Vẽ đồ thị các hàm số sau:
a) \(y = \frac{{{x^2} + x - 1}}{{x - 1}}\)
b) \(y = \frac{{ - {x^2} + x - 1}}{{x - 1}}\)
c) \(y = \frac{{{x^2} + 3x + 1}}{{x + 1}}\)
Vẽ đồ thị các hàm số sau:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
b) \(y = \frac{{ - x + 1}}{{x - 1}}\)
Vẽ đồ thị các hàm số bậc ba sau:
a) \(y = {x^3}\)
b) \(y = {x^3} - 3x\)
c) \(y = - {x^3} + 3x\)
d) \(y = {x^3} - 3x + 2\)
Thực hành 1 trang 89







Danh sách bình luận