Vẽ đồ thị các hàm số bậc ba sau:
a) \(y = {x^3}\)
b) \(y = {x^3} - 3x\)
c) \(y = - {x^3} + 3x\)
d) \(y = {x^3} - 3x + 2\)
Thực hành 1 trang 89
B1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org/ để sử dụng phiên bản online.
B2. Các bước thao tác trên GeoGebra:
– Tạo các thanh trượt biểu thị các tham số a, b, c, bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.
– Nhập công thức hàm số vào vùng nhập lệnh theo cú pháp: y = ax^3+bx+c
a) Đồ thị hàm số \(y = {x^3}\)

b) Đồ thị hàm số \(y = {x^3} - 3x\)
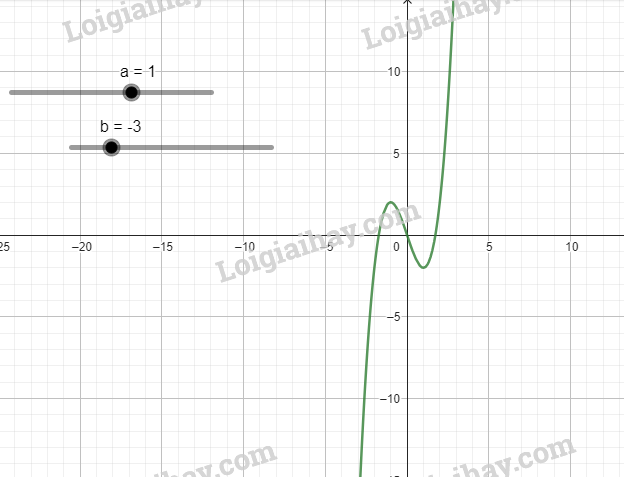
c) Đồ thị hàm số \(y = - {x^3} + 3x\)
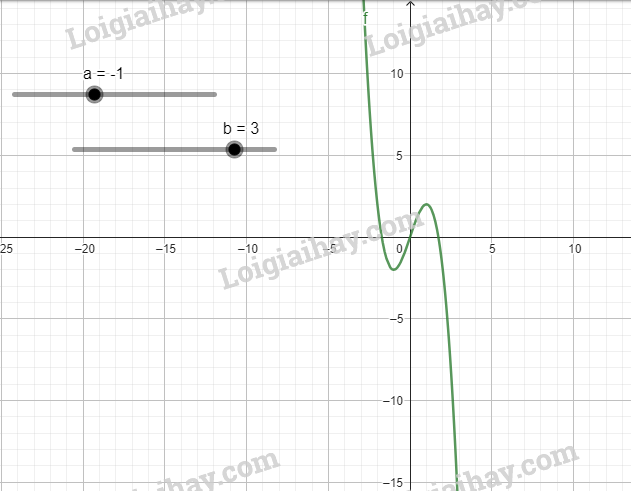
d) Đồ thị hàm số \(y = {x^3} - 3x + 2\)
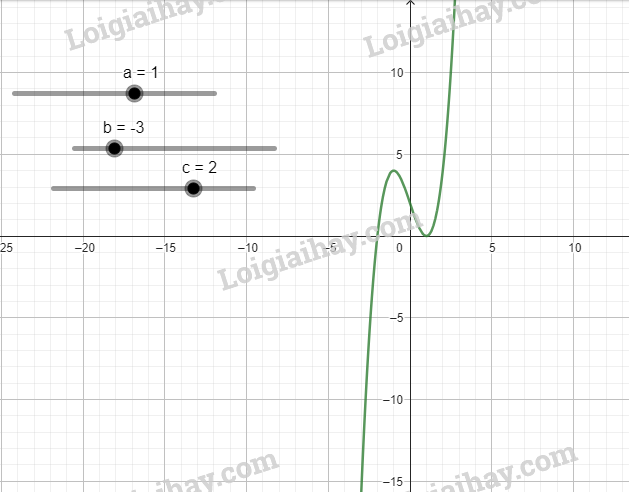

Các bài tập cùng chuyên đề
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Cho các hàm số đa thức sau:
(1) \(y = 3{x^2} + \sqrt 3 x + 1\); (2) \(y = {x^3} - 6{x^2} + 9\), (3) \(y = {x^4} - 4{x^2} + 3\).
a) Tìm đạo hàm cấp một và đạo hàm cấp hai của các hàm số trên.
b) Tìm tất cả các điểm cực trị của các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Cho các hàm số phân thức hữu tỉ sau:
(1) \(y = \frac{x}{{x + \sqrt 2 }}\); (2) \(y = \frac{{2x - 1}}{{x + 1}}\); (3) \(y = \frac{{{x^2} - 2x - 8}}{{x - 1}}\); \(y = 5x + 1 + \frac{3}{{2x - 3}}\).
a) Tìm đạo hàm cấp một của các hàm số trên.
b) Tìm các đường tiệm cận của đồ thị các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\).
b) \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\).
c) \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\).
d) \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
Vẽ đồ thị các hàm số sau:
a) \(y = \frac{{{x^2} + x - 1}}{{x - 1}}\)
b) \(y = \frac{{ - {x^2} + x - 1}}{{x - 1}}\)
c) \(y = \frac{{{x^2} + 3x + 1}}{{x + 1}}\)
Vẽ đồ thị các hàm số sau:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
b) \(y = \frac{{ - x + 1}}{{x - 1}}\)
Cho hàm số \(y = f(x) = {x^3} - 3{x^2} + 3\)
a) Sử dụng phần mềm GeoGebra vẽ đồ thị (C) của hàm số đã cho.
b) Tìm nghiệm gần đúng (làm tròn đến hàng phần trăm) của phương trình \(f(x) = 0\)
c) Dựa vào đồ thị đã vẽ ở câu a, biện luận theo tham số m số nghiệm của phương trình \({x^3} - 3{x^2} + 3 = m\).







Danh sách bình luận