Tìm tập hợp ước chung của
a) 30 và 45.
b) 42 và 70.
Tìm ước chung lớn nhất của các số, tập hợp ước chung là ước của ƯCLN.
a) \(30 = 2.3.5{\rm{ ; 45 = }}{{\rm{3}}^2}.5\)
Suy ra ƯCLN(30;45) = 15
Do đó ƯC(30;45) = Ư(15) = {1;3;5;15}.
b) \(42 = 2.3.7{\rm{ ; 70 = 2}}.5.7\)
Suy ra ƯCLN(42;70) = 14
Do đó ƯC(42;70) = Ư(14) = {1;2;7;14}.
Các bài tập cùng chuyên đề
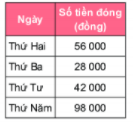
Vào ngày thứ Bảy, cô Lan tổ chức cho học sinh đi tham quan Bảo tàng Dân tộc học. Các học sinh đóng tiền mua vé, mỗi em một vé. Số tiền cô Lan thu được từng ngày được ghi lại ở bảng bên.
a) Hỏi số tiền để mua một vé (giá vé được tính theo đơn vị nghìn đồng) có thể là bao nhiêu, biết giá vé lớn hơn 2 000 đồng?
b) Có bao nhiêu học sinh tham gia chuyến đi, biết số học sinh trong lớp trong khoảng từ 20 đến 40 người?
Biết ƯCLN(75, 105) = 15, hãy tìm ƯC(75, 105).
a) Ta có ƯCLN(18, 30) = 6. Hãy viết tập hợp A các ước của 6. Nêu nhận xét về tập hợp ƯC(18, 30) và tập hợp A.
b) Cho hai số a và b. Để tìm tập hợp ƯC(a, b), ta có thể tìm tập hợp các nước của ƯCLN(a, b).
Hãy tìm ƯCLN rồi tìm tập hợp các ước chung của:
i. 24 và 30; ii. 42 và 98;
iii. 180 và 234.
Tìm ƯCLN(126, 150). Từ đó hãy tìm tất cả các ước chung của 126, 150
Quan sát bảng sau:
a) Viết tập hợp ƯC(24,36).
b) Tìm ƯCLN(24,36)
c) Thực hiện phép chia ƯCLN(24,36) cho các ước chung của hai số đó.
Tìm UCLN rồi tìm các ước chung của:
a) 16 và 24
b) 180 và 234
c) 60, 90 và 135
Hãy tìm ước chung lớn nhất rồi tìm ước chung của các số sau:
a) 72 và 90;
b) 200; 245 và 125.
Tuấn và Hà mỗi người mua một số hộp bút chì màu, trong đó mỗi hộp đều có từ hai chiếc bút trở lên và số bút trong mỗi hộp là như nhau. Tính ra Tuấn mua 25 bút, Hà mua 20 bút. Hỏi mỗi hộp bút chì màu có bao nhiêu chiếc?
a) Tìm các ước chung của 18, 27, 30, từ đó tìm ước chung lớn nhất của chúng
b) Tìm ước chung lớn nhất của 51,102, 144, từ đó tìm các ước chung của chúng
Tìm số tự nhiên a biết:
a) 388 chia cho a thì dư 38, còn 508 chia cho a thì dư 18;
b) 1 012 và 1 178 khi chia cho d đều có số dư bằng 16.
Cho hai số a=72 và b=96.
a) Phân tích a và b ra thừa số nguyên tố;
b) Tìm ƯCLN(a;b), rồi tìm ƯC(a,b).
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử.
\(A = \left\{ {x \in \mathbb{N}\,|\,60\; \vdots \;x,\;100\; \vdots \;x} \right.\) và \(\left. {x > 6} \right\}\);
