Trong các số thập phân sau, số nào là số thập phân hữu hạn? Số nào là số thập phân vô hạn tuần hoàn ?
0,1 ; -1,(23); 11,2(3); -6,725.
Xét các chữ số ở phần thập phân (đứng sau dấu phẩy).
Số 0,1 có một chữ số sau dấu phẩy nên 0,1 là số thập phân hữu hạn.
Số -6,725 có ba chữ số sau dấu phẩy nên -6,725 là số thập phân hữu hạn.
Số -1,(23) viết đầy đủ -1,232323..., có nhóm hai chữ số 23 được lặp lại mãi. Vì vậy số -1,(23) là số thập phân vô hạn tuần hoàn.
Số 11,2(3) viết đầy đủ 11,2333..., có chữ số 3 được lặp lại mãi. Vì vậy số 11,2(3) là số thập phân vô hạn tuần hoàn.

Các bài tập cùng chuyên đề
Thay dấu “?” bằng chữ số thích hợp.
So sánh:
a) 12,26 và 12,(24);
b) 31,3(5) và 29,9(8)
Chọn phát biểu đúng trong các phát biểu sau:
\(a)\sqrt 2 \in I;\,\,\,\,\,b)\sqrt 9 \in I;\,\,\,\,c)\,\pi \in I;\,\,\,\,\,d)\sqrt 4 \in \mathbb{Q}\)

Chữ số thập phân thứ 221 sau dấu “,” của số hữu tỉ \(\dfrac{1}{7}\) được viết dưới dạng số thập phân vô hạn tuần hoàn là chữ số nào?
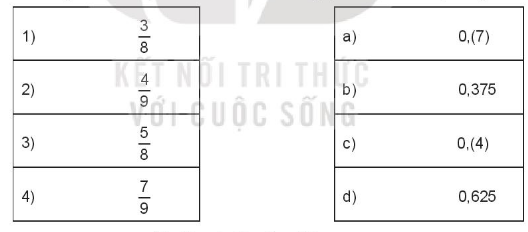
Nối mỗi phân số ở cột bên trái với cách viết thập phân của nó ở cột bên phải:
Sắp xếp các số sau theo thứ tự tăng dần: \(\sqrt {\dfrac{1}{{16}}} ;{\rm{ }}4\dfrac{1}{7};{\rm{ }}1,(3);{\rm{ }}\sqrt {81} ;{\rm{ }} - \sqrt {25} ;{\rm{ }} - 12,1\).
So sánh
a) 12,26 và 12,(24)
b) 31,3(5) và 29,9(8)
So sánh:
a) \(213,6(42)\) và \(213,598...\);
b) \( - 43,001\) và \( - 43,(001)\);
c) \( - \sqrt {237} \) và \( - 15\);
d) \(\sqrt {1\dfrac{{40}}{{81}}} \) và \(\sqrt {1\dfrac{{20}}{{101}}} \);
e) \(2 + \sqrt {37} \) và \(6 + \sqrt 2 \);
g) \(\dfrac{{\sqrt {{5^2}} + \sqrt {{{15}^2}} }}{{\sqrt {{4^2}} + \sqrt {{{36}^2}} }}\) và \(\dfrac{1}{{\sqrt {{2^2}} }}\).
Sắp xếp các số sau theo thứ tự tăng dần:
a) \( - 0,34;{\rm{ }} - 6,(25);{\rm{ }}1\dfrac{5}{9};{\rm{ }}\sqrt {169} ;{\rm{ }}\sqrt {15} \);
b) \(1,0(09);{\rm{ }}\sqrt {64} ;{\rm{ }}31\dfrac{1}{5};{\rm{ }} - 34,(5);{\rm{ }} - \sqrt {225} \).
Sắp xếp các số sau theo thứ tự giảm dần:
a) \(2\dfrac{1}{4};{\rm{ }}\sqrt {16} ;{\rm{ }} - \sqrt {83} ;{\rm{ }} - \sqrt {196} ;{\rm{ }} - 0,0(51);\)
b) \(21\dfrac{1}{6};{\rm{ }}\sqrt {49} ;{\rm{ }} - \sqrt {144} ;{\rm{ }} - 614,1;{\rm{ }} - 111,0(3).\)

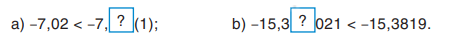






Danh sách bình luận