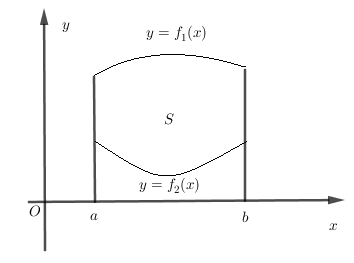
Cho hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và có đồ thị như hình vẽ bên. Gọi $S$ là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng \(x = a,x = b\). Thể tích $V$ của vật thể tròn xoay tạo thành khi quay $S$ quanh trục $Ox$ được tính bởi công thức nào sau đây ?
-
A.
\(V = \pi \int\limits_a^b {\left( {f_1^2(x) - f_2^2(x)} \right)} dx\).
-
B.
\(V = \pi \int\limits_a^b {\left( {{f_1}(x) - {f_2}(x)} \right)} dx\).
-
C.
\(V = \int\limits_a^b {\left( {f_1^2(x) - f_2^2(x)} \right)} dx\).
-
D.
\(V = \pi \int\limits_a^b {{{\left( {{f_1}(x) - {f_2}(x)} \right)}^2}} dx\).
Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng \(\left( H \right)\) giới hạn bởi các đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) liên tục trên \(\left[ {a;b} \right],0 \le f\left( x \right) \le g\left( x \right),\forall x \in \left[ {a;b} \right]\) quay quanh trục \(Ox\)
Công thức tính: \(V = \pi \int\limits_a^b {\left[ {{g^2}\left( x \right) - {f^2}\left( x \right)} \right]dx} \)
Theo công thức trên ta có: \(V = \pi \int\limits_a^b {\left( {f_1^2(x) - f_2^2\left( x \right)} \right)} dx\) (vì đồ thị hàm số \(y = {f_1}\left( x \right)\) nằm phía trên đồ thị hàm số \(y = {f_2}\left( x \right)\).
Đáp án : A
Một số em sẽ chọn nhầm đáp án C vì quên không nhân thêm \(\pi \) vào công thức tính thể tích.
Hs có thể chọn nhầm đáp án D vì nghĩ rằng $f^2(x)-g^2(x)=(f(x)-g(x))^2$ là sai.








Danh sách bình luận