Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường $y = \sqrt {2 - x} ;y = x$ xung quanh trục $Ox$ được tính theo công thức nào sau đây?
-
A.
$V = \pi \int\limits_0^2 {(2 - x)dx + \pi \int\limits_0^2 {{x^2}} } dx$
-
B.
$V = \pi \int\limits_0^2 {(2 - x)dx} $
-
C.
$V = \pi \int\limits_0^1 {xdx + \pi \int\limits_1^2 {\sqrt {2 - x} } } dx$
-
D.
$V = \pi \int\limits_0^1 {{x^2}dx + \pi \int\limits_1^2 {(2 - x)} } dx$
Thể tích khối tròn xoay có được khi quay hình phẳng giới hạn bởi các đường $y = f\left( x \right);y = g\left( x \right);x = a;x = b$ xung quanh trục $Ox$ được tính theo công thức: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \)
Thể tích khối tròn xoay cần tìm là thể tích khối tròn xoay khi quay 2 hình phẳng $(H_1)$ và $(H_2)$ quanh trục $Ox$ trong đó $(H_1)$ giới hạn bởi đường thẳng $y = x; x = 0; x = 1$ và $(H_2)$ được giới hạn bởi các đường $y = \sqrt {2 - x} ;x = 1;x = 2$.
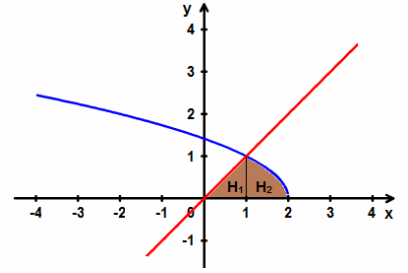
Khi đó ta có:
Thể tích $V$ cần tính chính bằng thể tích $V_1$ của khối tròn xoay thu được khi quay hình $(H_1)$ xung quanh trục $Ox$ cộng với thể tích $V_2$ của khối tròn xoay thu được khi quay hình $(H_2)$ xung quanh trục $Ox:$
$V = \pi \int\limits_0^1 {{x^2}dx} + \pi \int\limits_1^2 {(2 - x)dx} $
Đáp án : D
