Tính lực kéo cần thiết để kéo một khẩu pháo có trọng lượng 22 148 N (ứng với khối lượng xấp xỉ 2 260kg) lên một con dốc nghiêng \({30^o}\) so với phương nằm ngang (H.4.18). Nếu lực kéo của mỗi người bằng 100N, thì cần tối thiểu bao nhiêu người để kéo pháo?
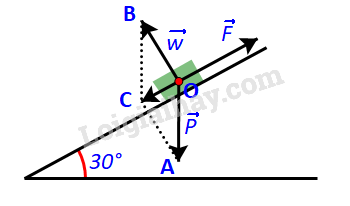
Khi cân bằng lực (trọng lực, phản lực, lực kéo) thì khẩu pháo đứng yên, do đó để kéo được khẩu pháo lên thì lực kéo phải lớn hơn hoặc bằng tổng hợp lực của trọng lực và phản lực.
Tìm hướng và độ lớn của tổng hợp lực giữa trọng lực và phản lực, từ đó suy ra độ lớn của lực kéo.
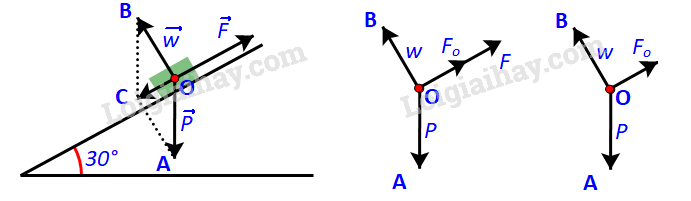
Khẩu pháo chịu tác động của ba lực: trọng lực \(\overrightarrow P \)(kí hiệu \(\overrightarrow {OA} \)), phản lực \(\overrightarrow w \)(kí hiệu \(\overrightarrow {OB} \)) và lực kéo \(\overrightarrow F \). Để kéo pháo thì độ lớn của lực kéo phải lớn hơn độ lớn của lực kéo khi pháo cân bằng \(\overrightarrow {{F_o}} \)(kí hiệu \(\overrightarrow {O{F_o}} \) )
Khi pháo cân bằng thì: \(\overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow 0 \)
Để tổng hợp lực \(\overrightarrow P \) và \(\overrightarrow w \), ta vẽ hình bình hành OACB.
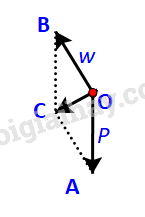
Ta có:
\(OB = \;AC;\;\;OB//\;AC\;\; \Rightarrow \overrightarrow {OB} = \;\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {AC} + \overrightarrow {OA} = \overrightarrow {OA} + \overrightarrow {AC} = \overrightarrow {OC} \)
\( \Rightarrow \overrightarrow 0 = \overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {O{F_o}} = \overrightarrow {OC} + \overrightarrow {O{F_o}} \)
\( \Rightarrow \;O\) là trung điểm của \(C{F_o}\), hay \(OC = \left| {\overrightarrow {{F_o}} } \right|\).
Lại có: \(OB \bot \;\;OC\)(do \(\overrightarrow {OB} \) là phản lực)
\( \Rightarrow \;AC \bot CO \Rightarrow OC = OA\,.\,\,\cos \widehat {AOC}\)
Mà \(\widehat {AOC} = {90^o} - {30^o} = {60^o}\); \(\left| {\overrightarrow P } \right| = OA = 22\;148\;N\)
\( \Rightarrow OC = 22\;148\,.\,\,\cos {60^o} = 11074\;\left( N \right)\)
Vậy lực \(\overrightarrow {{F_o}} \)có độ lớn là \(11\;074\;N\), để kéo pháo thì lực \(\overrightarrow F \) cùng hướng với \(\overrightarrow {{F_o}} \) và \(\left| {\overrightarrow F } \right| > 11\;074\;N\)
Vì \(11\;074\;:100 = 110,74\) nên cần tối thiểu 111 người để kéo pháo.

Các bài tập cùng chuyên đề
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 .\)
Cho tam giác ABC có M là trung điểm AC, N là trung điểm BC và AB = a. Tính độ dài vecto \(\overrightarrow {CM} - \overrightarrow {NB} \).
Cho hai vecto \(\overrightarrow a \),\(\overrightarrow b \). Lấy một điểm M tùy ý.
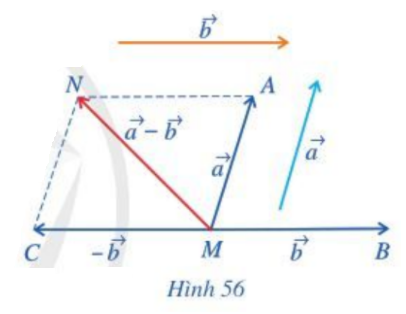
a) Vẽ \(\overrightarrow {MA} = \overrightarrow a ,\;\overrightarrow {MB} = \overrightarrow b ,\;\overrightarrow {MC} = - \overrightarrow b \) (Hình 56)
b) Tổng của hai vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) bằng vecto nào?
Cho ba điểm D, E, G. Vecto \(\overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} )\) bằng vecto nào sau đây?
A. \(\overrightarrow {EG} \)
B. \(\overrightarrow {GE} \)
C. \(\overrightarrow {GD} \)
D. \(\overrightarrow {ED} \)
Cho ABCD là hình bình hành. Chứng minh \(\overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD} \) với mỗi điểm M trong mặt phẳng.
Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} ;\)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\).
Tìm hợp lực của hai lực đối nhau \(\overrightarrow F \) và \( - \overrightarrow F \) (hình 11)







Danh sách bình luận