Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
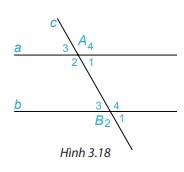
Hãy tính và so sánh hai góc so le trong còn lại A2 và B4.
Sử dụng tính chất 2 góc kề bù: Tổng 2 góc kề bù bằng 180 độ
+) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l}60^\circ + \widehat {{A_2}} = 180^\circ \\ \text{suy ra } \widehat {{A_2}} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
+) Vì \(\widehat {{B_3}} + \widehat {{B_4}} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l}60^\circ + \widehat {{B_4}} = 180^\circ \\ \text{suy ra } \widehat {{B_4}} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vậy hai góc so le trong còn lại A2 và B4 bằng nhau và bằng \(120^\circ \).

Các bài tập cùng chuyên đề
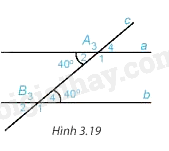
Quan sát Hình 3.19.
a) Biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
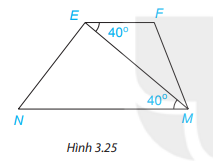
Quan sát Hình 3.25. Biết \(\widehat {MEF} = 40^\circ ;\widehat {EMN} = 40^\circ \). Em hãy giải thích tại sao EF // NM.
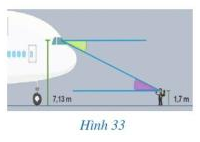
Hình 33 minh họa góc quan sát của người phi công và góc quan sát của người hoa tiêu khi hướng dẫn máy bay bay vào vị trí ở sân bay
Theo em dự đoán, hai góc đó có bằng nhau hay không?
Góc ở vị trí so le trong với \(\widehat {xMN}\) là
A. \(\widehat {yNt'}\)
B. \(\widehat {MNy'}\)
C. \(\widehat {xMt}\)
D. \(\widehat {NMx'}\).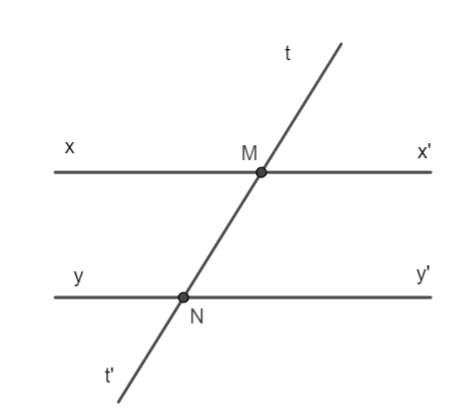
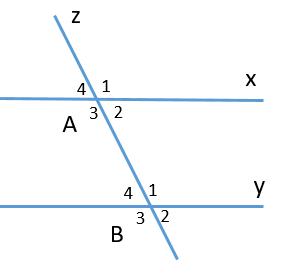
Biết một cặp góc so le trong \(\widehat {{A_2}}\; = \widehat {{B_4}} = 36^\circ \). Tính số đo của cặp góc so le trong còn lại:
-
A.
\(144^{o}\);
-
B.
\(136^{o}\);
-
C.
\(66^{o}\);
-
D.
\(64^{o}\).
Cho hình vẽ.
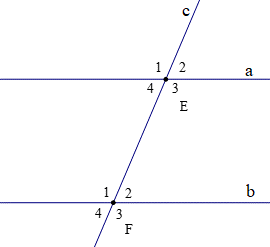
Chọn một cặp góc so le trong trong hình vẽ trên:
-
A.
\({\widehat {\rm{E}}_1}\) và \({\widehat {\rm{F}}_1}\);
-
B.
\({\widehat {\rm{E}}_2}\) và \({\widehat {\rm{F}}_4}\);
-
C.
\({\widehat {\rm{E}}_4}\) và \({\widehat {\rm{F}}_2}\);
-
D.
\({\widehat {\rm{E}}_3}\) và \({\widehat {\rm{F}}_2}\).
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.

-
A.
\({115^0}\)
-
B.
\({55^0}\)
-
C.
\({135^0}\)
-
D.
\({145^0}\)







Danh sách bình luận