Dùng phần mềm Geogebra vẽ đồ thị của các hàm số sau và tìm toạ độ giao điểm (nếu có) của hai đồ thị:
1. \(y = \frac{1}{3}{{\rm{x}}^2}\) và \(y = - x + \frac{1}{2}\)
2. \(y = \sqrt 2 {x^2}\) và \(y = 2x - \sqrt 3 \)
3. \(y = - 1,2{x^2}\) và \(y = 0,6x + 0,075\)
Bước 1. Vẽ đồ thị hàm số \(y = a{x^2}\).
Nhập lệnh y = ax^2.
Bước 2. Vẽ đồ thị hàm số y = ax + b.
Nhập lệnh y = ax + b.
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng  để tìm giao điểm của hai đồ thị.
để tìm giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
1. \(y = \frac{1}{3}{x^2}\) và \(y = - x + \frac{1}{2}\).
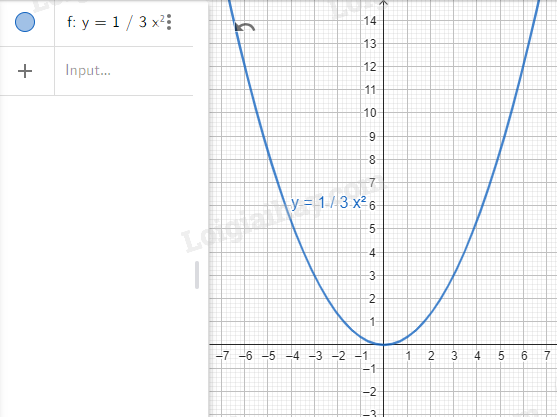
Bước 1. Vẽ đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
Nhập lệnh y = 1/3*x^2
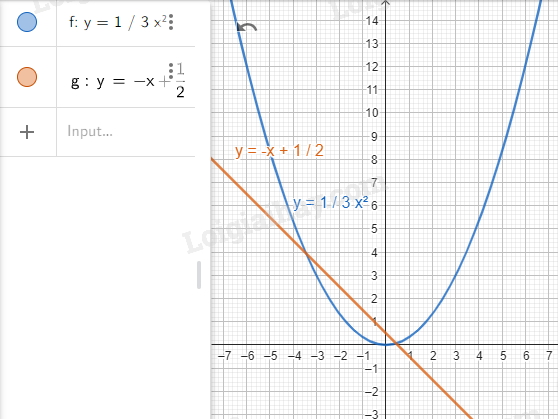
Bước 2. Vẽ đồ thị hàm số \(y = - x + \frac{1}{2}\).
Nhập lệnh y = -x + 1/2
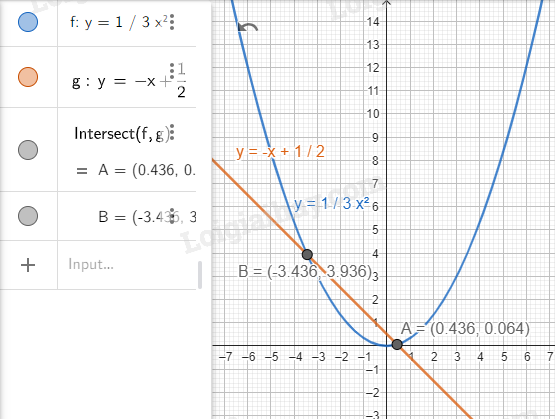
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng  để tìm giao điểm của hai đồ thị.
để tìm giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l}\frac{1}{3}{x^2} = - x + \frac{1}{2}\\\frac{1}{3}{x^2} + x - \frac{1}{2} = 0\end{array}\)
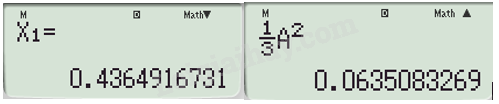
Ta được tọa độ điểm A.
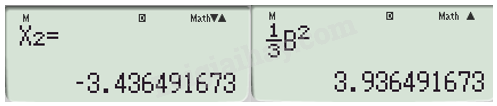
Ta được tọa độ điểm B.
2. \(y = \sqrt 2 {x^2}\) và \(y = 2x - \sqrt 3 \).
Bước 1. Vẽ đồ thị hàm số \(y = \sqrt 2 {x^2}\).
Sử dụng bàn phím của GeoGebra để nhập kí hiệu \(\sqrt {...} \)
Ta được màn hình như sau:

Nhập lệnh: \(y = \sqrt 2 *x\^2\)
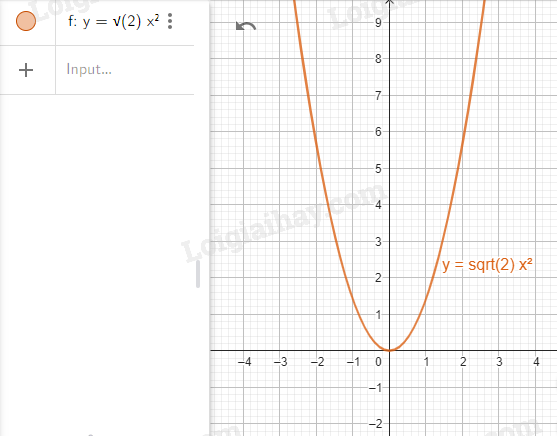
Bước 2. Vẽ đồ thị hàm số \(y = 2x - \sqrt 3 \).
Nhập lệnh \(y = 2x - \sqrt 3 \)
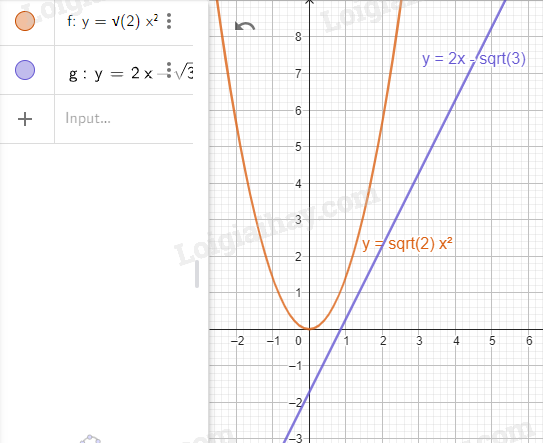
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng  ta thấy hai đồ thị không có điểm chung.
ta thấy hai đồ thị không có điểm chung.
Do đó không có giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l}\sqrt 2 {x^2} = 2x - \sqrt 3 \\\sqrt 2 {x^2} - 2x + \sqrt 3 = 0\end{array}\)
Sử dụng máy tính cầm tay để giải phương trình, ta được:
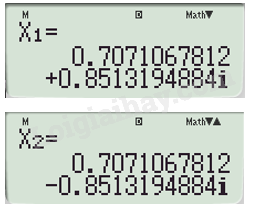
Vậy hai đồ thị không có giao điểm.
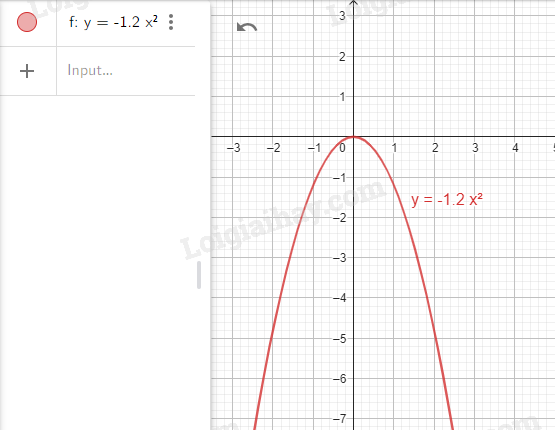
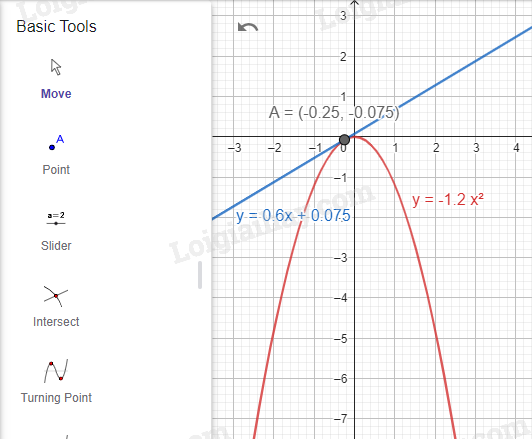
3. \(y = - 1,2{x^2}\) và \(y = 0,6x + 0,075\).
Bước 1. Vẽ đồ thị hàm số \(y = - 1,2{x^2}\).
Nhập lệnh y = -1.2*x^2
Bước 2. Vẽ đồ thị hàm số \(y = 0,6x + 0,075\).
Nhập lệnh \(y = 0.6x + 0.075\)
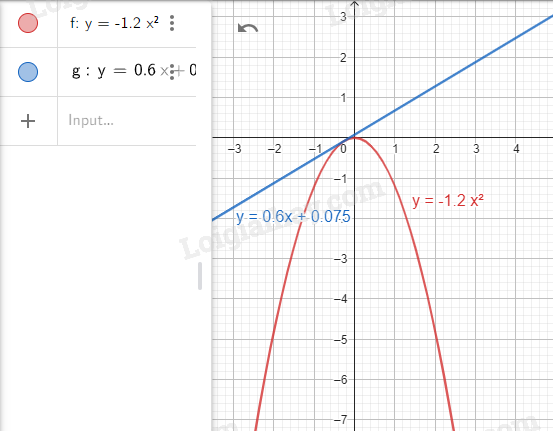
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng  để tìm giao điểm của hai đồ thị.
để tìm giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l} - 1,2{x^2} = 0,6x + 0,075\\ - 1,2{x^2} - 0,6x - 0,075 = 0\end{array}\)
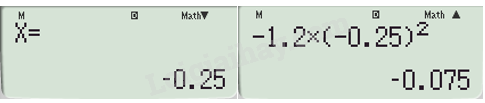
Ta được tọa độ điểm A.

Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \({x^2} - 4x + 10 = 0\);
b) \(x + \frac{9}{{x - 1}} = 7\);
c) \({x^2} - 2\left( {\sqrt 3 - 1} \right)x - 2\sqrt 3 = 0\);
d) \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} = \frac{4}{{{x^2} - 1}}\).
Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}3x - 2y = 4\\2x + y = 5\end{array} \right.\);
b) \(\left\{ \begin{array}{l}x + y = 5\\3x + \sqrt[3]{3}y = 6\end{array} \right.\);
c) \(\left\{ \begin{array}{l}3x + 2y = 0\\2x - 3y = 0\end{array} \right.\);
d) \(\left\{ \begin{array}{l}x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1\\\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1\end{array} \right.\).
Cho đường thẳng \(\left( d \right):y = 2x + \sqrt 3 \) và parabol \(\left( P \right):y = {x^2}\).
a) Vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d) và (P).
Vẽ đồ thị các hàm số sau:
a) y = –x2;
b) y = x2;
c) y = \(\frac{1}{5}\)x2;
d) y = –0,2x2.
Vẽ đồ thị các hàm số sau:
a) y = 2x2;
b) y = –4x2;
c) y = = 5x2;
d) y = –2,5x2;
e) y = \(\frac{7}{2}\)x2;
g) y = \( - \frac{8}{5}\)x2.
Chọn một điểm khác nằm trên parabol để lập công thức của hàm số tương ứng và so sánh với kết quả tìm được ở Bước 2.







Danh sách bình luận