Vẽ đồ thị các hàm số sau:
a) y = 2x2;
b) y = –4x2;
c) y = = 5x2;
d) y = –2,5x2;
e) y = \(\frac{7}{2}\)x2;
g) y = \( - \frac{8}{5}\)x2.
1.Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online.
2. Các bước thao tác trên GeoGebra:
- Tạo thanh trượt biểu thị tham số a bằng cách nhất chuột vào thanh công cụ
và vào vị trí màn hình nơi ta muốn đặt thanh trượt.
- Nhập công thức hàm số \(y = a{x^2}\) tại vùng nhập lệnh theo cú pháp \(y = a*x^2\).
- Quan sát đồ thị được vẽ trên vùng làm việc.
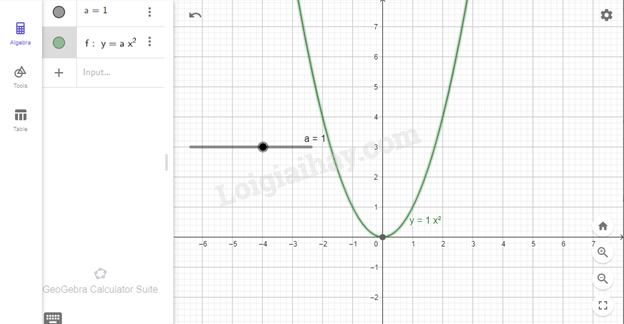
- Dùng chuột điều chỉnh thanh trượt a để có giá trị mong muốn.
- Quan sát sự thay đổi hình dạng của đồ thị (parabol) theo sự thay đổi của hệ số a.
- Chụp lại màn hình đồ thị.
a) Di chuyển điểm a đến a = 2, ta được đồ thị hàm số y = 2x2.
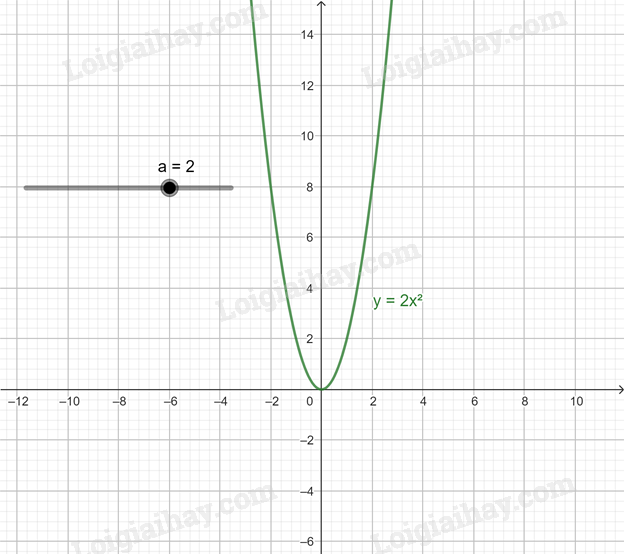
b) Di chuyển điểm a đến a = -4, ta được đồ thị hàm số y = –4x2
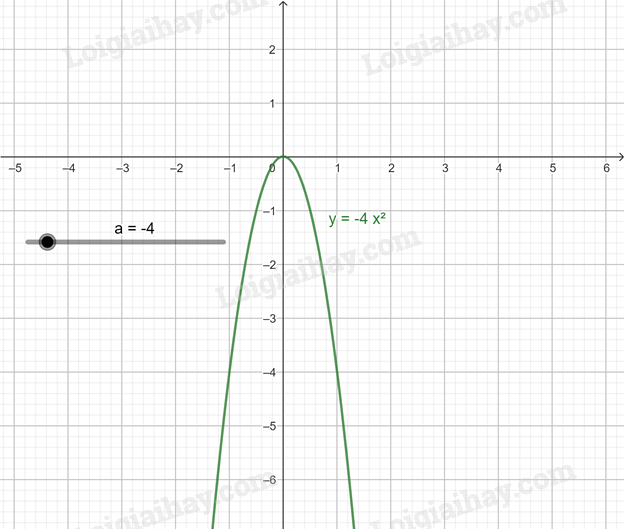
c) Di chuyển điểm a đến a = 5, ta được đồ thị hàm số y = = 5x2
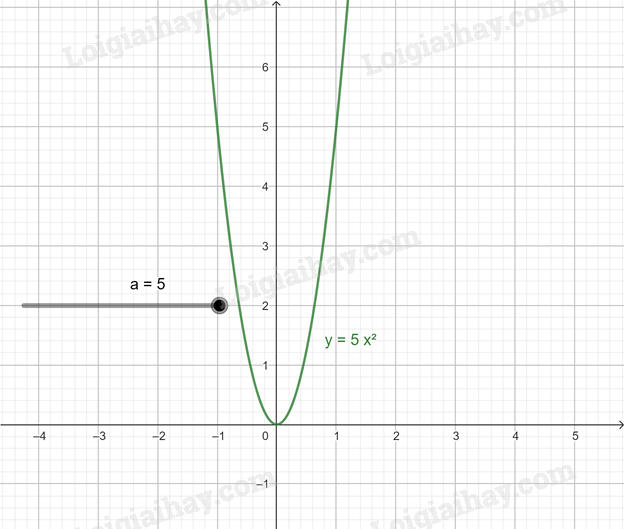
d) Di chuyển điểm a đến a = -2,5 , ta được đồ thị hàm số y = –2,5x2
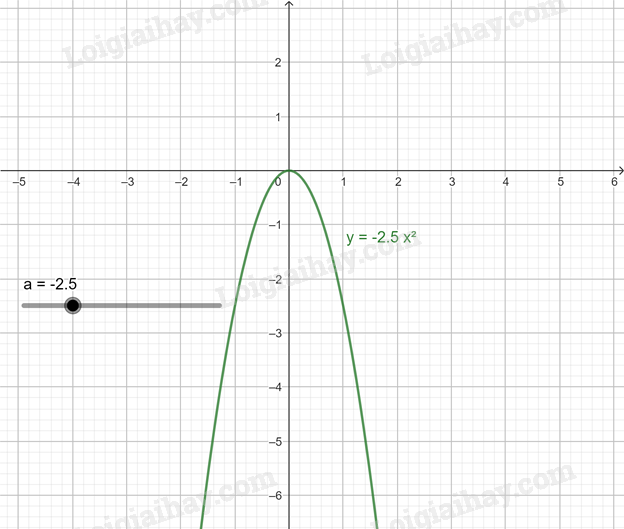
e) Di chuyển điểm a đến a = \(\frac{7}{2}\) = 3,5, ta được đồ thị hàm số y = \(\frac{7}{2}\)x2
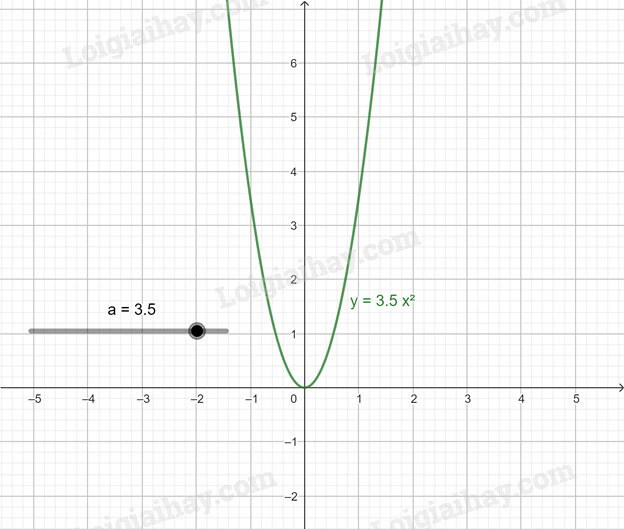
g) Di chuyển điểm a đến a = \( - \frac{8}{5}\) = -1,6, ta được đồ thị hàm số y = \( - \frac{8}{5}\)x2
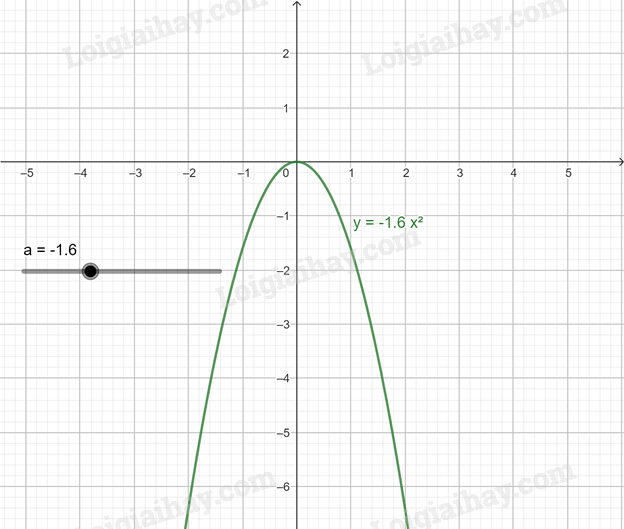

Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \({x^2} - 4x + 10 = 0\);
b) \(x + \frac{9}{{x - 1}} = 7\);
c) \({x^2} - 2\left( {\sqrt 3 - 1} \right)x - 2\sqrt 3 = 0\);
d) \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} = \frac{4}{{{x^2} - 1}}\).
Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}3x - 2y = 4\\2x + y = 5\end{array} \right.\);
b) \(\left\{ \begin{array}{l}x + y = 5\\3x + \sqrt[3]{3}y = 6\end{array} \right.\);
c) \(\left\{ \begin{array}{l}3x + 2y = 0\\2x - 3y = 0\end{array} \right.\);
d) \(\left\{ \begin{array}{l}x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1\\\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1\end{array} \right.\).
Cho đường thẳng \(\left( d \right):y = 2x + \sqrt 3 \) và parabol \(\left( P \right):y = {x^2}\).
a) Vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d) và (P).
Vẽ đồ thị các hàm số sau:
a) y = –x2;
b) y = x2;
c) y = \(\frac{1}{5}\)x2;
d) y = –0,2x2.
Dùng phần mềm Geogebra vẽ đồ thị của các hàm số sau và tìm toạ độ giao điểm (nếu có) của hai đồ thị:
1. \(y = \frac{1}{3}{{\rm{x}}^2}\) và \(y = - x + \frac{1}{2}\)
2. \(y = \sqrt 2 {x^2}\) và \(y = 2x - \sqrt 3 \)
3. \(y = - 1,2{x^2}\) và \(y = 0,6x + 0,075\)
Chọn một điểm khác nằm trên parabol để lập công thức của hàm số tương ứng và so sánh với kết quả tìm được ở Bước 2.







Danh sách bình luận