Tròn nói: Không cần giải, tớ biết ngay tổng và tích hai nghiệm của phương trình ${x^2} - x + 1 = 0$ đều bằng 1. Ý kiến của em thế nào?

Tìm $m$ để phương trình ${x^2} - 2\left( {m + 1} \right)x + 4m = 0$ ($x$ là ẩn, $m$ là tham số) có hai nghiệm ${x_1},{x_2}$ thỏa mãn $x_1^3 - x_1^2 = x_2^3 - x_2^2$.

Từ kết quả HĐ1, hãy tính ${x_1} + {x_2}$ và ${x_1}{x_2}$.

Không giải phương trình, hãy tính biệt thức $\Delta$ (hoặc $\Delta$’) để kiểm tra điều kiện có nghiệm, rồi tính tổng và tích các nghiệm của các phương tình bậc hai sau:

a) $2{x^2} - 7x + 3 = 0$;

b) $25{x^2} - 20x + 4 = 0$;

c) $2\sqrt 2 {x^2} - 4 = 0$.

Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của các phương trình sau:

a) ${x^2} - 12x + 8 = 0$;

b) $2{x^2} + 11x - 5 = 0$;

c) $3{x^2} - 10 = 0$;

d) ${x^2} - x + 3 = 0$.

Chứng tỏ rằng nếu phương trình bậc hai $a{x^2} + bx + c = 0$ có hai nghiệm là ${x_1}$ và ${x_2}$ thì đa thức $a{x^2} + bx + c$ được phân tích được thành nhân tử sau: $a{x^2} + bx + c = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)$.

Áp dụng: Phân tích các đa thức sau thành nhân tử:

a) ${x^2} + 11x + 18$;

b) $3{x^2} + 5x - 2$.

Phương trình bậc hai có hai nghiệm ${x_1} = 13$ và ${x_2} = 25$ là

A. ${x^2} - 13x + 25 = 0$.

B. ${x^2} - 25x + 13 = 0$.

C. ${x^2} - 38x + 325 = 0$.

D. ${x^2} + 38x + 325 = 0$.

Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình ${x^2} - 5x + 6 = 0$. Khi đó, giá trị của biểu thức $A = x_1^2 + x_2^2$ là

A. 13.

B. 19.

C. 25.

D. 5.

Cho phương trình ${x^2} - 11x + 30 = 0$. Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình. Không giải phương trình, hãy tính:

a) $x_1^2 + x_2^2$;

b) $x_1^3 + x_2^3$.

Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình bậc hai ${x^2} - 5x + 3 = 0$. Không giải phương trình, hãy tính:

a) $x_1^2 + x_2^2$;

b) ${\left( {{x_1} - {x_2}} \right)^2}$.

Cho phương trình $a{x^2} + bx + c = 0(a \ne 0)$ có hai nghiệm ${x_1},{x_2}$.

Tính ${x_1} + {x_2}$ và ${x_1}.{x_2}$.

Tính tổng và tích các nghiệm (nếu có) của mỗi phương trình:

a) ${x^2} - 2\sqrt 7 x + 7 = 0$

b) $15{x^2} - 2x - 7 = 0$

c) $35{x^2} - 12x + 2 = 0$

Cho phương trình ${x^2} + 4x - 21 = 0$. Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của các biểu thức:

a) $\frac{2}{{{x_1}}} + \frac{2}{{{x_2}}}$

b) ${x_1}^2 + {x_2}^2 - {x_1}.{x_2}$

Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình:

a) $3{x^2} - 9x + 5 = 0$

b) $25{x^2} - 20x + 4 = 0$

c) $5{x^2} - 9x + 15 = 0$

d) $5{x^2} - 2\sqrt 3 x - 3 = 0$

Cho phương trình ${x^2} - 19x - 5 = 0$. Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của các biểu thức:

a) A = ${x_1}^2 + {x_2}^2$

b) B = $\frac{2}{{{x_1}}} + \frac{2}{{{x_2}}}$

c) C = $\frac{3}{{{x_1} + 2}} + \frac{3}{{{x_2} + 2}}$

Gọi S và P lần lượt là tổng và tích của hai nghiệm của phương trình ${x^2} + 5x - 10 = 0$. Khi đó giá trị của S và P là

A. S = 5; P = 10.

B. S = - 5; P = 10.

C. S = -5; P = -10.

D. S = 5; P = -10.

Cho phương trình ${x^2} + 7x - 15 = 0$. Gọi ${x_1};{x_2}$ là hai nghiệm của phương trình. Khi đó giá trị của biểu thức ${x_1}^2 + {x_2}^2 - {x_1}{x_2}$là

A. 79

B. 94

C. -94

D. -79

Cho phương trình $2{x^2} - 7x + 6 = 0$. Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của các biểu thức:

A = $\left( {{x_1} + 2{x_2}} \right)\left( {{x_2} + 2{x_1}} \right) - {x_1}^2{x_2}^2$

Xét phương trình $a{x^2} + bx + c = 0(a \ne 0)$. Giả sử phương trình đó có 2 nghiệm là ${x_1},{x_2}.$ Tính ${x_1} + {x_2};{x_1}.{x_2}$ theo các hệ số $a,b,c.$

Cho phương trình $- 4{x^2} + 9x + 1 = 0$.

a)   Chứng minh phương trình có 2 nghiệm phân biệt ${x_1},{x_2}.$

b)  Tính ${x_1} + {x_2};{x_1}.{x_2}$.

c)   Tính ${x_1}^2 + {x_2}^2$.

Nếu ${x_1},{x_2}$ là hai nghiệm của phương trình $a{x^2} + bx + c = 0(a \ne 0)$ thì:

a)   ${x_1} + {x_2} =  - \frac{b}{a};{x_1}.{x_2} =  - \frac{c}{a}$

b)  ${x_1} + {x_2} = \frac{c}{a};{x_1}.{x_2} =  - \frac{b}{a}$

c)   ${x_1} + {x_2} = \frac{b}{a};{x_1}.{x_2} =  - \frac{c}{a}$

d)  ${x_1} + {x_2} =  - \frac{b}{a};{x_1}.{x_2} = \frac{c}{a}$

Giải thích vì sao nếu $ac < 0$ thì phương trình $a{x^2} + bx + c = 0(a \ne 0)$ có 2 nghiệm là 2 số trái dấu nhau.

Giải thích vì sao nếu phương trình $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$ có hai nghiệm ${x_1},{x_2}$ thì $a{x^2} + bx + c = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)$.

Áp dụng phân tích các đa thức sau thành nhân tử:

a)    ${x^2} - 2x - 3$

b)   $3{x^2} + 5x - 2$

Xét phương trình $a{x^2} + bx + c = 0(a \ne 0)$. Giả sử phương trình có nghiệm x₁, x₂, so sánh S = x₁ + x₂ và $- \frac{b}{a}$, $P = {x_1}{x_2}$ và $\frac{c}{a}$.

Không giải phương trình, chứng minh phương trình ${x^2} + 3x - 6 = 0$ có hai nghiệm phân biệt x₁ , x₂ và tính M = x₁ + x₂ - x₁x₂ .

Cho phương trình ${x^2} - 2\sqrt 5 x + 3 = 0$

a) Không giải phương trình, chứng minh phương trình đã cho có hai nghiệm phân biệt x₁ , x₂ .

b) Tính $\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}};{x_1}^2 + {x_2}^2.$

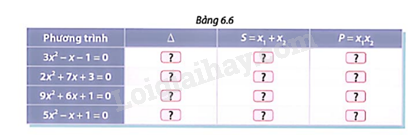
Với mỗi phương trình ở Bảng 6.6:

a) Tìm các số thích hợp cho mỗi ô ? ở cột $\Delta$.

b) Nếu phương trình có nghiệm ${x_1};{x_2}$, không giải phương trình, hãy tìm các số thích hợp cho mỗi ô ? ở cột S và P.

Cho phương trình $3{x^2} - 10x + 3 = 0$.

a) Không giải phương trình, chứng minh phương trình có hai nghiệm ${x_1},{x_2}$.

b) Tính $(2{x_1} - 1)(2{x_2} - 1);\left| {{x_1} - {x_2}} \right|.$

Cho phương trình $3{x^2} - x - 1 = 0$ có hai nghiệm ${x_1},{x_2}$. Không giải phương trình, hãy tính giá trị của các biểu thức sau:

A = $\left( {3{x_1} - 1} \right)(3{x_2} - 1)$

B = ${x_1}^2 + {x_2}^2$

Cho phương trình bậc hai (ẩn x): ${x^2} - 4x + m - 2 = 0$.

a) Tìm điều kiện của ẩn m để phương trình có nghiệm.

b) Với các giá trị m tìm được ở câu a, gọi ${x_1}$ và ${x_2}$ là hai nghiệm của phương trình. Hãy tính giá trị của các biểu thức sau theo m: $A = x_1^2 + x_2^2;B = x_1^3 + x_2^3$.

Giả sử phương trình bậc hai $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$ có hai nghiệm là ${x_1}$, ${x_2}$ đều khác 0. Hãy lập phương trình bậc hai có hai nghiệm là $\frac{1}{{{x_1}}}$ và $\frac{1}{{{x_2}}}$.