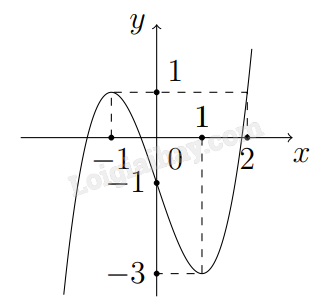
Cho hàm số \(f\left( x \right)\) có đồ thị như hình bên. Phương trình \(f\left[ {f\left( {\cos x} \right) - 1} \right] = 0\) có bao nhiêu nghiệm thuộc đoạn \(\left[ {0;2\pi } \right]\)?
-
A.
\(2\).
-
B.
\(5\).
-
C.
\(4\).
-
D.
\(6\).
Giao điểm của đồ thị hàm số \(y{\rm{ }} = {\rm{ }}f\left( x \right)\) và \(y{\rm{ }} = {\rm{ }}g\left( x \right)\) có tọa độ là nghiệm của hệ phương trình \(y{\rm{ }} = {\rm{ }}f\left( x \right)\) và \(y{\rm{ }} = {\rm{ }}g\left( x \right)\).
Phương trình hoành độ giao điểm: cho \(f\left( x \right) = g\left( x \right)\) (1)
Số giao điểm của 2 đồ thị bằng nghiệm của phương trình (1).
Tương giao đồ thị hàm số \(y = f\left( x \right)\) và trục hoành
Ta có phương trình hoành độ giao điểm như sau: \(f\left( x \right) = 0\)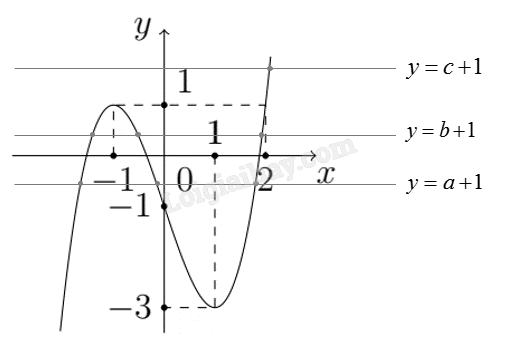
Dựa vào đồ thị hàm số ta thấy:
\(f\left[ {f\left( {\cos x} \right) - 1} \right] = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( {\cos x} \right) - 1 = a \in \left( { - 2; - 1} \right)\\f\left( {\cos x} \right) - 1 = b \in \left( { - 1;0} \right)\\f\left( {\cos x} \right) - 1 = c \in \left( {1;2} \right)\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}f\left( {\cos x} \right) = a + 1 \in \left( { - 1;0} \right)\\f\left( {\cos x} \right) = b + 1 \in \left( {0;1} \right)\\f\left( {\cos x} \right) = c + 1 \in \left( {2;3} \right)\end{array} \right.\)
• Xét phương trình \(f\left( {\cos x} \right) = a + 1 \Leftrightarrow \left[ \begin{array}{l}\cos x = {\alpha _1} < - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\cos x = {\alpha _2} \in \left( { - 1;0} \right)\,\,\,\,\,\,\left( 2 \right)\\\cos x = {\alpha _3} > 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)
Vì \(\cos x \in \left[ { - 1;1} \right]\) nên phương trình \(\left( 1 \right),\,\left( 3 \right)\) vô nghiệm và phương trình \(\left( 2 \right)\) có 2 nghiệm thuộc đoạn \(\left[ {0;2\pi } \right]\).
• Xét phương trình \(f\left( {\cos x} \right) = b + 1 \Leftrightarrow \left[ \begin{array}{l}\cos x = {\beta _1} < - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\\\cos x = {\beta _2} \in \left( { - 1;0} \right)\,\,\,\,\,\,\,\left( 5 \right)\\\cos x = {\beta _3} > 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 6 \right)\end{array} \right.\)
Vì \(\cos x \in \left[ { - 1;1} \right]\) nên phương trình \(\left( 4 \right),\,\left( 6 \right)\) vô nghiệm và phương trình \(\left( 5 \right)\) có 2 nghiệm thuộc đoạn \(\left[ {0;2\pi } \right]\).
• Xét phương trình \(f\left( {\cos x} \right) = c + 1 \Leftrightarrow \cos x = t > 2\)
Nhận xét hai nghiệm của phương trình \(\left( 5 \right)\) không trùng với nghiệm nào của phương trình \(\left( 2 \right)\) nên phương trình \(f\left[ {f\left( {\cos x} \right) - 1} \right] = 0\) có 4 nghiệm phận biệt.
Đáp án : C








Danh sách bình luận