Giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2{\cos ^2}x - 2\sqrt 3 \sin x.\cos x + 1\) trên đoạn \(\left[ {0,\frac{{7\pi }}{{12}}} \right]\) lần lượt là
-
A.
\(\mathop {\min y}\limits_{\left[ {0,\frac{{7\pi }}{{12}}} \right]} = 2;\mathop {\max y}\limits_{\left[ {0,\frac{{7\pi }}{{12}}} \right]} = 3\).
-
B.
\(\mathop {\min y}\limits_{\left[ {0,\frac{{7\pi }}{{12}}} \right]} = 0;\mathop {\max y}\limits_{\left[ {0,\frac{{7\pi }}{{12}}} \right]} = 3\).
-
C.
\(\mathop {\min y}\limits_{\left[ {0,\frac{{7\pi }}{{12}}} \right]} = 0;\mathop {\max y}\limits_{\left[ {0,\frac{{7\pi }}{{12}}} \right]} = 4\).
-
D.
\(\mathop {\min y}\limits_{\left[ {0,\frac{{7\pi }}{{12}}} \right]} = 0;\mathop {\max y}\limits_{\left[ {0,\frac{{7\pi }}{{12}}} \right]} = 2\).
Dựa vào sự biến thiên của các hàm số lượng giác
\(y = 2{\cos ^2}x - 2\sqrt 3 \sin x.\cos x + 1 = \cos 2x + \sqrt 3 \sin 2x + 2 = 2\cos \left( {2x - \frac{\pi }{3}} \right) + 2\)
ta có \(y = 2\cos \left( {2x + \frac{\pi }{3}} \right) + 2\). Đặt \(u = 2x + \frac{\pi }{3}\)
Từ đề bài ta xét \(x \in \left[ {0;\frac{{7\pi }}{{12}}} \right] \Rightarrow u \in \left[ {\frac{\pi }{3};\frac{{3\pi }}{2}} \right]\)
Ta lập BBT của hàm số \(y = 2\cos u + 2\) trên \(\left[ {\frac{\pi }{3};\frac{{3\pi }}{2}} \right]\).
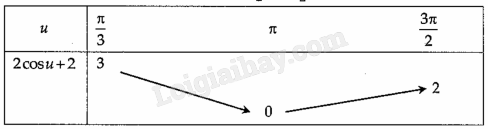
Từ bảng biến thiên ta thấy \(\mathop {\min }\limits_{\left[ {\frac{\pi }{3};\frac{{3\pi }}{2}} \right]} f(u) = 0\,\,{\rm{khi}}\,\,u = \pi \Leftrightarrow x = \frac{\pi }{3}\)
\(\mathop {\max }\limits_{\left[ {\frac{\pi }{3};\frac{{3\pi }}{2}} \right]} f(u) = 3\,\,{\rm{khi}}\,\,u = \frac{\pi }{3} \Leftrightarrow x = 0\)
Hay \(\mathop {\min }\limits_{\left[ {0;\frac{{7\pi }}{{12}}} \right]} y = 0;\mathop {{\rm{max}}}\limits_{\left[ {0;\frac{{7\pi }}{{12}}} \right]} y = 3\).
Đáp án : B








Danh sách bình luận