Một bánh xe có $72$ răng. Số đo góc mà bánh xe đã quay được khi di chuyển $10$ răng là:
-
A.
${30^o}.$
-
B.
${40^o}.$
-
C.
${50^o}.$
-
D.
${60^o}.$
- Tính độ dài \(10\) răng (cung tròn chứa \(10\) răng).
- Sử dụng công thức tính độ dài cung tròn \(l = \alpha R\) để tính số đo góc (đơn vị radian).
- Sử dụng công thức liên hệ giữa độ và radian để tính góc theo đơn vị độ.
$72$ răng có chiều dài là \(2\pi R\) nên $10$ răng có chiều dài:
\(l = \dfrac{{10.2\pi R}}{{72}} = \dfrac{{5\pi }}{{18}}R\).
Theo công thức tính độ dài cung tròn, ta có:
\(l = R\alpha \Leftrightarrow \alpha = \dfrac{l}{R} = \dfrac{{\dfrac{5}{{18}}\pi R}}{R} = \dfrac{5}{{18}}\pi \).
Đổi đơn vị đo góc:
\(\alpha = \frac{5}{{18}}\pi = {\left( {\frac{{180.\frac{5}{{18}}\pi }}{\pi }} \right)^o} = {50^o}\).
Đáp án : C
Cách khác: $72$ răng tương ứng với \({360^0}\) nên $10$ răng tương ứng với $\dfrac{{10.360}}{{72}} = {50^0}$.
Chu vi hình tròn
Hình tròn bán kính R có chu vi là \(2\pi R\).
Độ dài cung tròn
Một cung của đường tròn bán kính R, số đo \({\alpha ^o}\) có độ dài:
\(l = \frac{{\pi R\alpha }}{{180}}\)
Một cung của đường tròn bán kính R, số đo \(\alpha \) (rad) có độ dài:
\(l = R\alpha \)

Các bài tập cùng chuyên đề
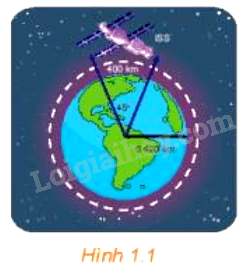
Trạm vũ trụ Quốc tế ISS (tên Tiếng Anh: International Space Station) nằm trong quỹ đạo tròn cách bề mặt Trái Đất khoảng 400 km (H.1.1). Nếu trạm mặt đất theo dõi được trạm vũ trụ ISS khi nó nằm trong góc 45° ở tâm của quỹ đạo tròn này phía trên ăng-ten theo dõi, thì trạm vũ trụ ISS đã di chuyển được bao nhiêu kilômét trong khi nó đang được trạm mặt đất theo dõi? Giả sử rằng bán kính của Trái Đất là 6 400 km. Làm tròn kết quả đến hàng đơn vị.
Cho đường tròn bán kính R.
a) Độ dài của cung tròn có số đo bằng 1 rad là bao nhiêu
b) Tính độ dài l của cung tròn có số đo \(\alpha \)rad.
Một đường tròn có bán kính 20 cm. Tính độ dài của các cung trên đường tròn đó có số đo sau:
a) \(\frac{\pi }{{12}}\);
b) \(1,5\);
c) \({35^0}\);
d) \({315^0}\).
Một đường tròn có bán kính 20m. Tìm độ dài của cung trên đường tròn đó có số đo là
a) \(\frac{{2\pi }}{7}\);
b) \({36^0}\).
Kim giờ dài 6cm và kim phút dài 11cm của đồng hồ chỉ 4 giờ. Hỏi thời gian ít nhất để 2 kim vuông góc với nhau là bao nhiêu? Lúc đó tổng quãng đường 2 đầu mút kim giờ và kim phút đi được là bao nhiêu?
Kim phút và kim giờ của đồng hồ lớn nhà Bưu điện Thành phố Hà Nội theo thứ tự dài 1,75 m và 1,26 m. Hỏi trong 15 phút, mũi kim phút vạch nên cung tròn có độ dài bao nhiêu mét? Cũng câu hỏi đó cho mũi kim giờ.
Huyện lị Quản Bạ tỉnh Hà Giang và huyện lị Cái Nước tỉnh Cà mau cùng nằm ở \({105^0}\) kinh đông, nhưng Quản Bạ ở \({23^0}\) vĩ bắc, Cái Nước ở vĩ độ \({9^0}\) bắc. Hãy tính độ dài cung kinh tuyến nối hai huyện lị đó (khoảng cách theo đường chim bay), coi Trái đất có bán kính 6378km.
Trong chặng đua nước rút, bánh xe của một vận động viên đua xe đạp quay được 30 vòng trong 8 giây. Chọn chiều quay của bánh xe là chiều dương. Xét van V của bánh xe.
a) Sau 1 phút, van V đó quay được một góc có số đo bao nhiêu radian?
b) Biết rằng bán kính của bánh xe là 35cm. Độ dài quãng đường mà vận động viên đua xe đạp đã đi được trong 1 phút là bao nhiêu mét?
Một cung tròn có độ dài bằng bán kính. Khi đó số đo bằng radian của cung tròn đó là
-
A.
1
-
B.
2
-
C.
\(\pi \)
-
D.
\(2\pi \)
Trên đường tròn, cung có số đo 1 rad là?
-
A.
Cung có độ dài bằng 1.
-
B.
Cung tương ứng với góc ở tâm \({60^o}\).
-
C.
Cung có độ dài bằng đường kính.
-
D.
Cung có độ dài bằng nửa đường kính.
Cho đường tròn có bán kính 6 cm. Tính số đo (rad) của cung có độ dài 3 cm.
-
A.
1
-
B.
0,5
-
C.
2
-
D.
3
Cho đường tròn O đường kính bằng 10 cm. Tính độ dài cung có số đo \(\dfrac{{7\pi }}{{12}}\).
-
A.
\(\dfrac{{35\pi }}{6}\) cm
-
B.
\(\dfrac{{17\pi }}{3} \) cm
-
C.
\(\dfrac{{35\pi }}{2}\)
-
D.
\(\dfrac{{35\pi }}{{12}}\)
Tính độ dài cung tròn có bán kính R = 20 cm và có số đo 135o.
-
A.
2700 cm
-
B.
\(27\pi\) cm
-
C.
\(15\pi\) cm
-
D.
155 cm
Một đường tròn có bán kính R = 75cm. Độ dài của cung trên đường tròn đó có số đo \(\alpha = \dfrac{\pi }{{25}}\) là:
-
A.
\(3\pi \) cm
-
B.
\(4\pi \) cm
-
C.
\(5\pi \) cm
-
D.
\(6\pi \) cm
Sân bay Quốc tế Cát Bi – Hải Phòng và sân bay Quốc tế Tân Sơn Nhất – TP Hồ Chí Minh nằm xấp xỉ trên một kinh tuyến. Biết rằng sân bay Quốc tế Cát Bi có vĩ độ là Bắc, sân bay Quốc tế Tân Sơn Nhất có vĩ độ Bắc. Biết rằng bán kính trái đất tại xích đạo là 6378 km. Khoảng cách giữa hai sân bay trên là bao nhiêu km (kết quả làm tròn đến hàng đơn vị)?
Bánh xe đạp có bán kính 50cm. Một người quay bánh xe 5 vòng quanh trục thì quãng đường đi được là:
-
A.
\(250\pi (cm)\)
-
B.
\(1000\pi (cm)\)
-
C.
\(500\pi (cm)\)
-
D.
\(200\pi (cm)\)
Một đồng hồ treo tường, kim giờ dài 11cm. Trong 40 phút mũi kim giờ vạch lên cung tròn có độ dài là:
-
A.
3,8 cm
-
B.
3,82 cm
-
C.
3,84 cm
-
D.
3,86 cm
Một đường tròn có bán kính 15 cm. Tìm độ dài cung tròn có góc ở tâm bằng \({30^o}\).
-
A.
\(\frac{{5\pi }}{2}\)
-
B.
\(\frac{{5\pi }}{3}\)
-
C.
\(\frac{{2\pi }}{5}\)
-
D.
\(\frac{\pi }{3}\)
Một cung có độ dài 10 cm, có số đo bằng radian là 2,5 thì đường tròn của cung đó có bán kính là
-
A.
2,5 cm
-
B.
3,5 cm
-
C.
4 cm
-
D.
4,5 cm
Một đồng hồ treo tường, kim giờ dài 10,57 cm. Trong 30 phút mũi kim giờ vạch lên cung tròn có độ dài là:
-
A.
2,77 cm
-
B.
2,9 cm
-
C.
2,76 cm
-
D.
2,8 cm
Một đồng hồ treo tường, kim giờ dài \(10,57{\rm{ cm}}\). Trong 30 phút mũi kim giờ vạch lên cung tròn có độ dài là:
-
A.
\(2,77{\rm{ cm}}\).
-
B.
\(2,9{\rm{ cm}}\).
-
C.
\(2,76{\rm{ cm}}\).
-
D.
\(2,8{\rm{ cm}}\).
Một cung tròn có độ dài bằng 2 lần bán kính. Số đo radian của cung tròn đó là
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Bánh xe đạp có bán kính 50 cm. Một người quay bánh xe 5 vòng quanh trục thì quãng đường đi được là
-
A.
\(250\pi\) cm.
-
B.
\(1000\pi \) (cm).
-
C.
\(500\pi\) (cm).
-
D.
\(200\pi\) (cm).







Danh sách bình luận