Bài 3.5: Kiểm định giả thuyết thống kê - Chuyên đề Tin học 12 Chân trời sáng tạo

1

Trả lời câu hỏi Khởi động trang 89 Chuyên đề Tin học 12 Chân trời sáng tạo

Từ dữ liệu Bằng 1, bạn A có nhận xét rằng giá trị trung bình điểm môn Toán của học sinh lớp 12 là 4.9 điểm. Nhận xét này có đúng không? Giải thích?

Lời giải chi tiết:

Từ dữ liệu Bằng 1, bạn A có nhận xét rằng giá trị trung bình điểm môn Toán của học sinh lớp 12 là 4.9 điểm. Nhận xét này có đúng hay không phải xem xét các nội dung sau:

- Thu thập dữ liệu: Liệt kê tất cả điểm môn Toán của học sinh, bỏ qua các mục không có điểm số (NT).

- Tính điểm trung bình: Sử dụng công thức

Điểm Trung Bình=Số lượng điểm/Tổng điểm Toán

trong Excel để tính giá trị trung bình.

- So sánh và kết luận: So sánh kết quả với nhận xét của bạn A và đưa ra kết luận.

1

Trả lời câu hỏi trang 90 Chuyên đề Tin học 12 Chân trời sáng tạo

Trong Excel để kiểm định giả thuyết thống kê về trung bình với một giá trị, em sử dụng hàm nào

Lời giải chi tiết:

Trong Excel để kiểm định giả thuyết thống kê về trung bình với một giá trị, em sử dụng hàm T.TEST.

- Hàm T.TEST trong Excel được sử dụng để tính xác suất liên quan đến kiểm định T. Nó trả về xác suất của kiểm định T Student. Kiểm định T thường được sử dụng để so sánh trung bình của hai mẫu hoặc một mẫu với một giá trị đã biết.

Cú pháp: =T.TEST(array1, array2, tails, type)

2

Trả lời câu hỏi trang 91 Chuyên đề Tin học 12 Chân trời sáng tạo

Trong Excel để kiểm định giả thuyết thống kê về sự khác biệt giữa hai trung bình tổng thể, em sử dụng công cụ nào?

Lời giải chi tiết:

Trong Excel để kiểm định giả thuyết thống kê về sự khác biệt giữa hai trung bình tổng thể, em sử dụng công cụ: Data Analysis (Phân tích dữ liệu) với tùy chọn t-Test: Two-Sample Assuming Equal Variances hoặc t-Test: Two-Sample Assuming Unequal Variances.

Luyện tập Câu 1

Trả lời câu hỏi Luyện tập 1 trang 91 Chuyên đề Tin học 12 Chân trời sáng tạo

Trả lời câu hỏi Luyện tập 1 trang 91 Chuyên đề Tin học 12 Chân trời sáng tạo

Lời giải chi tiết:

Trong Excel Hàm T.DIST.2T trả về phân bố t hai phía. Phân bố t hai phía được sử dụng trong kiểm định giả thuyết khi bạn muốn kiểm tra sự khác biệt giữa các giá trị trung bình của hai mẫu mà không biết phương sai của chúng và không giả định rằng các mẫu có phương sai bằng nhau.

Vậy đáp án đúng: C. T.DIST.2T

Luyện tập Câu 2

Trả lời câu hỏi Luyện tập 2 trang 91 Chuyên đề Tin học 12 Chân trời sáng tạo

Khi sử dụng công cụ t-Test: Two-Sample Assuming Unequal Variances, để xuất kết quả phân tích sang một trang mới, em thực hiện tuỳ chọn nào?

A. Output Range.

B. New Worksheet Ply.

C. New Workbook.

D. New Sheet.

Lời giải chi tiết:

Khi sử dụng công cụ t-Test: Two-Sample Assuming Unequal Variances, để xuất kết quả phân tích sang một trang mới, em thực hiện tuỳ chọn: New Worksheet Ply

Khi sử dụng công cụ t-Test: Two-Sample Assuming Unequal Variances trong Excel và bạn muốn xuất kết quả phân tích sang một trang mới, bạn cần chọn tùy chọn New Worksheet Ply. Tùy chọn này sẽ xuất kết quả phân tích sang một trang tính mới trong cùng một sổ làm việc hiện tại.

Vậy đáp án đúng: B. New Worksheet Ply

Nhiệm vụ Câu 1

Trả lời câu hỏi Nhiệm vụ 1 trang 92 Chuyên đề Tin học 12 Chân trời sáng tạo

Kiểm định giả thuyết thống kê về trung bình với một giá trị

Yêu cầu: Kiểm định giả thuyết thống kê "Giá trị trung bình điểm môn Toán của học sinh lớp 12 là 4.9 điểm" với một mẫu ngẫu nhiên gồm 40 học sinh (Bảng 1) có phần phối chuẩn, mức ý nghĩa là 0.05. Nhận xét của bạn A ở KHỞI ĐỘNG có đúng không?

Lời giải chi tiết:

Để thực hiện, em cần tìm số liệu thống kê kiểm tra và so sánh với giá trị p để xem liệu giá trị trung bình điểm Toán của học sinh lớp 12 là 4.9 điểm có đúng hay không. Em sử dụng các hàm COUNT, AVERAGE, STDEV.P, SQRT, TDIST.2T. Các bước thực hiện như sau:

1. Giả thuyết H = 4.9, giả thuyết H # 4.9. Chọn vùng chứa kết quả và thực hiện nhập công thức tính toán các nội dung (Hình 3):

- Mức ý nghĩa: Tại ô tính J2, nhập giá trị 0.05 (Giá trị đã cho).

Giả thuyết: Tại ô tính J3, nhập giá trị 4.9 (Giá trị em cần kiểm định, giả thuyết gốc Hạ).

- Số mẫu: Tại ô tính J4, nhập công thức =COUNT(E2:E42) (Đếm số mẫu).

- Trung bình: Tại ô tính J5, nhập công thức =AVERAGE(E2:E42) (Tính trung bình mẫu). Độ lệch chuẩn: Tại ô tính J6, nhập công thức =STDEV.P(E2:E42).

- Giá trị t: Tại ô tính J8, nhập công thức =(J5-J3)*SQRT(J4)/J6.

- Giá trị p: Tại ô tính J9, nhập công thức =T.DIST.2T(J8,J4-1),

2. Sau khi thiết lập các công thức em được kết quả như Hình 4.

3. Quan sát kết quả trả về trong ô tính J9, nhận thấy giá trị p=0.72>0.05 nên chấp nhận giả thuyết Ho.

Như vậy, nhận xét của bạn A ở Khởi động về giá trị trung bình điểm môn Toán của học sinh lớp 12 là 4.9 điểm là đúng.

Nhiệm vụ Câu 2

Trả lời câu hỏi Nhiệm vụ 2 trang 92 Chuyên đề Tin học 12 Chân trời sáng tạo

Kiểm định giả thuyết thống kê về sự khác biệt giữa hai trung bình tổng thể

Yêu cầu: Quan sát dữ liệu Bảng 1, bạn A nhận xét rằng giá trị trung bình điểm môn Ngũ văn cao hơn môn Toán. Bạn B thì cho rằng giá trị trung bình điểm môn Ngữ văn bằng môn Toán. Theo em, với mức ý nghĩa 0.01, nhận xét của bạn nào đúng?

Lời giải chi tiết:

1. Từ yêu cầu đề bài em xác định giả thuyết H, H = ụ (điểm trung binh môn Ngữ văn bằng điểm trung bình môn Toán), giả thuyết H, I_ * H, (điểm trung bình môn Ngữ văn cao hơn điểm trung bình môn Toán) với vị L là các biến ngẫu nhiên của điểm Ngữ văn và Toán.

1a. Nhảy chọn thẻ Data, chọn Data Analysis.

1b. Trong hộp thoại Data Analysis, nhảy chọn t-Test: Two-Sample Assuming Unequal Variances, chon OK.

1c. Trong hộp thoại t-Test: Two-Sample Assuming Unequal Variances, thiết lập các tuy chọn như sau (Hình 5):

Input:

Variable 1 Range: $F$2:$F$42 (vùng chứa dữ liệu điểm Ngữ văn).

Variable 2 Range: $E$2:$E$42 (vùng chứa dữ liệu điểm Toán).

Nháy chọn mục Labels.

Alpha: 0.01.

Output Range: $I$2 (vùng chứa kết quả).

1c. Nhảy chọn OK.

2. Quan sát Ifish 6, dòng P(T<=t) two-tail = 0,004 < 0.01 nên bác bỏ H, chấp nhận H. Như vậy, điểm trung bình môn Ngữ văn cao hơn điểm trung bình môn Toán. Do dó nhận xét của bạn A đúng.

Vận dụng Câu 1

Trả lời câu hỏi Vận dụng 1 trang 93 Chuyên đề Tin học 12 Chân trời sáng tạo

Độ dài chi tiết máy (đơn vị: cm) là biến ngẫu nhiên X có phân phối chuẩn. Kiểm tra 28 sản phẩm thu được số liệu như sau:

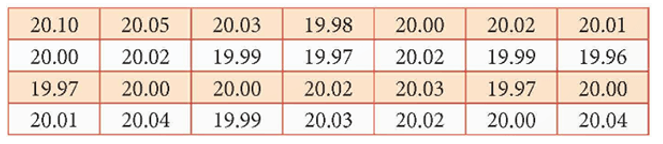
Với mức ý nghĩa 0.05 có thể cho rằng trung bình độ dài chi tiết máy bằng 20 cm hay không?

Lời giải chi tiết:

Để kiểm định với mức ý nghĩa 0.05 có thể cho rằng trung bình độ dài chi tiết máy bằng 20 cm hay không ta thực hiện như sau:

- Nhập Dữ Liệu: Đưa tất cả số liệu đo được vào một cột trong Excel.

- Tính Giá Trị Trung Bình Mẫu ( ( \bar{x} ) ): Sử dụng công thức =AVERAGE(range) trong Excel, thay range bằng dãy ô chứa dữ liệu.

- Tính Độ Lệch Chuẩn Mẫu ( ( s ) ): Dùng công thức =STDEV.S(range).

- Thực hiện Kiểm Định T: Sử dụng công thức: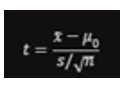 

- So Sánh Giá Trị T: So sánh giá trị t tính được với giá trị t từ bảng phân phối t của Student tại bậc tự do ( n-1 ) và mức ý nghĩa 0.05.

Vận dụng Câu 2

Trả lời câu hỏi Vận dụng 2 trang 94 Chuyên đề Tin học 12 Chân trời sáng tạo

Người ta tiến hành một cuộc khảo sát về giá của hai cửa hàng thực phẩm lớn trong thành phố, 12 mặt hàng thông dụng nhất được chọn ngẫu nhiên và giá của chúng bán ở hai cửa hang được ghi lại như sau:

Với mức ý nghĩa 2%, có sự khác nhau về giá cả trung bình của các mặt hàng ở hai cửa hang hay không?

Lời giải chi tiết:

Người ta tiến hành một cuộc khảo sát về giá của hai cửa hàng thực phẩm lớn trong thành phố, 12 mặt hàng thông dụng nhất được chọn ngẫu nhiên và giá của chúng bán ở hai cửa hang được ghi lại như sau:

Muốn kiểm định xem có sự khác biệt về giá cả trung bình giữa hai cửa hàng hay không với mức ý nghĩa 2%, ta làm như sau:

- Nhập giá của 12 mặt hàng từ cửa hàng A và B vào hai cột riêng biệt.

- Sử dụng công thức =AVERAGE(range) để tính giá trung bình cho mỗi cửa hàng.

- Sử dụng công thức =T.TEST(array1, array2, tails, type) trong đó array1 và array2 là dãy giá từ cửa hàng A và B, tails là 2 (cho kiểm định hai đuôi), và type là 2 (cho hai mẫu độc lập).

- Nếu giá trị p thu được từ kiểm định nhỏ hơn 0.02, có thể kết luận rằng có sự khác biệt đáng kể về giá cả trung bình giữa hai cửa hàng.