Số thập phân là gì? Cách chuyển phân số, hỗn số thành số thập phân - Toán 5

Các phân số thập phân $\frac{1}{{10}}$ ; $\frac{1}{{100}}$ ; $\frac{1}{{1000}}$ được viết thành 0,1 ; 0,01 ; 0,001

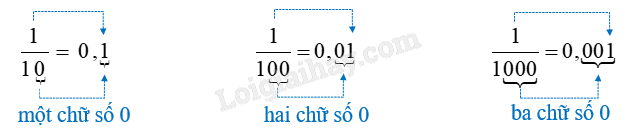
Các số 0,1; 0,01; 0,001 được gọi là số thập phân.

Tương tự ta có:

$\frac{3}{{10}} = 0,3\,\,\,\,;\,\,\,\frac{5}{{100}} = 0,05$

$5\frac{1}{{10}} = 5,1\,\,\,;\,\,\,3\frac{{19}}{{1000}} = 3,019$

Các số 0,3 ; 0,5 ; 5,1 ; 3,019 ; ... là các số thập phân.

• Mỗi số thập phân gồm hai phần: phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.
• Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân

Ví dụ:

• Số gồm 2 đơn vị, 3 phần mười, 1 phần trăm, 5 phần nghìn

Viết là: 2,315 ; Đọc là: Hai phẩy ba trăm mười lăm

• Số gồm 0 đơn vị, 2 phần mười, 7 phần trăm, 9 phần nghìn

Viết là: 0,279 ; Đọc là: Không phẩy hai trăm bảy mươi chín

– Nếu phân số đã cho chưa là phân số thập phân thì ta chuyển các phân số thành phân số thập phân.

– Đếm xem mẫu số có bao nhiêu chữ số 0, thì dịch chuyển dấu phẩy về bên trái bấy nhiêu chữ số.

Ví dụ 1: Chuyển các phân số sau thành số thập phân

$\frac{8}{{10}}$                 $\frac{{15}}{{1000}}$                              $\frac{3}{{25}}$                             $\frac{7}{{125}}$

Cách giải

$\frac{8}{{10}} = 0,8$                                                       $\frac{{15}}{{1000}} = 0,015$                          

$\frac{3}{{25}} = \frac{{3 \times 4}}{{25 \times 4}} = \frac{{12}}{{100}} = 0,12$                               $\frac{7}{{125}} = \frac{{7 \times 8}}{{125 \times 8}} = \frac{{56}}{{1000}} = 0,056$

Ví dụ 2: Viết các hỗn số sau thành số thập phân

$2\frac{3}{{10}}$                          $5\frac{{21}}{{100}}$                             

$2\frac{4}{5}$                                 $1\frac{3}{4}$

Cách giải

$2\frac{3}{{10}} = 2,3$                                        $5\frac{{21}}{{100}} = 5,21$                             

$2\frac{4}{5} = 2\frac{8}{{10}} = 2,8$                         $1\frac{3}{4} = 1\frac{{75}}{{100}} = 1,75$