Hàm hợp là gì? Cách tính đạo hàm của hàm hợp - Toán 11

Giả sử hàm số \(u = g(x)\) xác định trên \((a;b)\) và lấy giá trị trên \((c;d)\); \(y = f(u)\) là hàm số của \(u\), xác định trên \((c;d)\) và lấy giá trị trên \(\mathbb{R}\). Khi đó, ta có thể lập được một hàm số mới xác định trên \((a;b)\) và lấy giá trị trên \(\mathbb{R}\) theo quy tắc như hình.

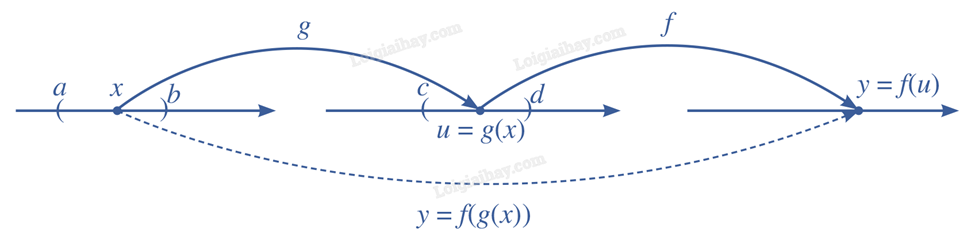
Hàm số \(y = f\left( {g(x)} \right)\) được gọi là hàm hợp của hai hàm số \(y = f(u)\), \(u = g(x)\).

Ví dụ minh hoạ:

1) Cho hàm số \(y = f(u) = \sqrt u \) và \(u = g(x) = x - 2\). Tìm hàm hợp \(y = f(g(x))\) và tập xác định của nó.

Giải:

Ta có: \(y = f(g(x)) = f(x - 2) = \sqrt {x - 2} \).

Hàm số trên xác định khi và chỉ khi  hay \(x \ge 2\). Tập xác định của hàm số đó là \([2; + \infty )\).

2) Mỗi hàm số sau đây là hàm hợp của hai hàm số nào?

a) \(y = \sin (2x + 3)\);

b) \(y = 2\sin x + 3\).

Giải:

a) Đặt \(u = 2x + 3,\) ta có: \(y = \sin u.\) Vậy \(y = \sin (2x + 3)\) là hàm hợp của hai hàm số \(y = \sin u\), \(u = 2x + 3.\)

b) Đặt \(u = \sin x,\) ta có: \(y = 2u + 3.\) Vậy \(y = 2\sin x + 3\) là hàm hợp của hai hàm số \(y = 2u + 3,\) \(u = \sin x.\)

Nếu hàm số \(u = g(x)\) có đạo hàm tại \(x\) là \({u_x}'\) và hàm số \(y = f(u)\) có đạo hàm tại \(u\) là \({y_u}'\) thì hàm hợp \(y = f\left( {g(x)} \right)\) có đạo hàm tại \(x\) là \({y_x}' = {y_u}'.{u_x}'\).

Ví dụ minh hoạ:

1) Tìm đạo hàm của mỗi hàm số sau:

a) \(y = {(3 - 2x)^4}\);

b) \(y = \cos (4x + 5)\).

Giải:

a) Đặt \(u = 3 - 2x\), ta có: \(y = {u^4}\). Khi đó: \({y_u}' = 4{u^3}\); \({u_x}' =  - 2\).

Theo công thức tính đạo hàm của hàm hợp, ta có:

\({y_{x'}} = {y_u}' \cdot {u_x}' = 4{u^3} \cdot ( - 2) =  - 8{u^3} =  - 8{(3 - 2x)^3}.\)

b) Đặt \(u = 4x + 5\), ta có \(y = \cos u\). Khi đó: \({y_u}' =  - \sin u\); \({u_x}' = 4\).

Theo công thức tính đạo hàm của hàm hợp, ta có:

\({y_x}' = {y_u}' \cdot {u_x}' = ( - \sin u) \cdot 4 =  - 4\sin u =  - 4\sin (4x + 5)\).

2) Tính đạo hàm của hàm số \(y = \sqrt {{x^2} + 1} \).

Giải:

Đặt \(u = {x^2} + 1\) thì \(y = \sqrt u \) và \({y'_u} = \frac{1}{{2\sqrt u }}\), \({u'_x} = 2x\).

Theo công thức đạo hàm của hàm số hợp, ta có:

\({y_x}' = {y_u}' \cdot {u_x}' = \frac{{2x}}{{2\sqrt {{x^2} + 1} }} = \frac{x}{{\sqrt {{x^2} + 1} }}\).

Vậy đạo hàm của hàm số đã cho là \(y' = \frac{x}{{\sqrt {{x^2} + 1} }}\).

Trong thực hành, ta thường trình bày ngắn gọn như sau:

\(y' = \left( {\sqrt {{x^2} + 1} } \right)' = \frac{{\left( {{x^2} + 1} \right)'}}{{2\sqrt {{x^2} + 1} }} = \frac{{2x}}{{2\sqrt {{x^2} + 1} }} = \frac{x}{{\sqrt {{x^2} + 1} }}\).

3) Tính đạo hàm của các hàm số sau:

a) \(y = {(3{x^2} + x)^3}\);

b) \(y = \sin 2x\);

c) \(y = {e^{{x^2} + 1}}\).

Giải:

a) Đặt \(u = 3{x^2} + x\) thì \(y = {u^3}\). Ta có \({u_x}' = 6x + 1\) và \({y_u}' = ({u^3})' = 3{u^2}\).

Suy ra \({y_x}' = {y_u}'\), \({u_{x'}} = 3{u^2}\). \((6x + 1) = 3{(3{x^2} + x)^2}\). \((6x + 1)\).

Vậy \(y' = 3{(3{x^2} + x)^2}\). \((6x + 1)\).

b) Đặt \(u = 2x\) thì \(y = \sin u\). Ta có \({u_x}' = 2\) và \({y_u}' = (\sin u)' = \cos u\).

Suy ra \({y_x}' = {y_u}'\), \({u_x}' = \cos u\), \(2 = 2\cos 2x\).

Vậy \(y' = 2\cos 2x\).

c) Đặt \(u = {x^2} + 1\) thì \(y = {e^u}\). Ta có \({u_x}' = 2x\) và \({y_u}' = ({e^u})' = {e^u}\).

Suy ra \({y_x}' = {y_u}'\), \({u_x}' = {e^u}\), \(2x = 2x{e^{{x^2} + 1}}\).

Vậy \(y' = 2x{e^{{x^2} + 1}}\).