Bài 3. Đơn vị và sai số trong Vật Lí trang 15, 16, 17, 18, 19, 20, 21, 22, 23 Vật Lí 10 Chân trời sáng tạo
Kể tên một số đại lượng vật lí và đơn vị của chúng mà các em đã được học trong môn Khoa học tự nhiên. Phân biệt đơn vị và thứ nguyên trong Vật lí. Phân tích thứ nguyên của khối lượng riêng ρ theo thứ nguyên của các đại lượng cơ bản. Từ đó cho biết đơn vị của ρ trong hệ SI.
Câu hỏi tr 15
Kể tên một số đại lượng vật lí và đơn vị của chúng mà các em đã được học trong môn Khoa học tự nhiên.
Phương pháp giải:
Vận dụng kiến thức đã học trong môn Khoa học tự nhiên
Lời giải chi tiết:
Một số đại lượng vật lí và đơn vị của chúng:
+ Quãng đường: m
+ Thời gian: s
+ Nhiệt độ: K
+ Khối lượng chất: mol
+ Năng lượng: J
+ Khối lượng: kg
...
Câu hỏi tr 16
Phân biệt đơn vị và thứ nguyên trong Vật lí.
Phương pháp giải:
Vận dụng kiến thức đã học
Lời giải chi tiết:
Thứ nguyên của một đại lượng là quy luật nêu lên sự phụ thuộc vào đơn vị đo đại lượng đó vào các đơn vị cơ bản.
Ví dụ: Tốc độ, vận tốc được biểu diễn bằng đơn vị m/s; km/h nhưng chỉ có một thứ nguyên là L.T-1
Câu hỏi tr 17 CH 3
Phân tích thứ nguyên của khối lượng riêng ρ theo thứ nguyên của các đại lượng cơ bản. Từ đó cho biết đơn vị của ρ trong hệ SI.
Phương pháp giải:
Thứ nguyên của một số đại lượng cơ bản
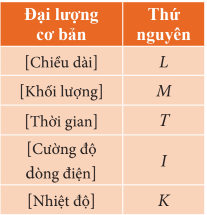
Các đơn vị cơ bản trong hệ SI
Biểu thức tính khối lượng riêng: \(\rho = \frac{m}{V}\)
Lời giải chi tiết:
Ta có thứ nguyên của khối lượng m là M, thứ nguyên của thể tích V là L3
=> Thứ nguyên của khối lượng riêng ρ là M.L-3
=> Đơn vị của ρ trong hệ SI là kg/m3
Câu hỏi tr 17 LT
Hiện nay có những đơn vị thường được dùng trong đời sống như picômét (pm), miliampe (mA) (ví dụ như kích thước của một hạt bui là khoảng 2,5 pm; cường độ dòng điện dùng châm cứu là khoảng 2 mA). Hãy xác định các đơn vị cơ bản và các tiếp đầu ngữ của 2 đơn vị trên.
Phương pháp giải:
Tên và kí hiệu tiếp đầu ngữ của bội số, ước số thập phân của đơn vị
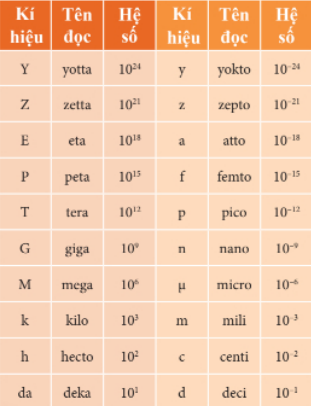
Lời giải chi tiết:
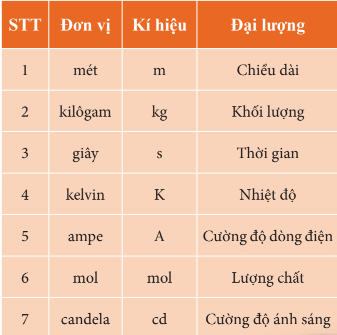
Đơn vị cơ bản của 2 đơn vị trên là: m và A
2,5 pm = 2,5.10-12 m
2 mA = 2.10-3 A
Câu hỏi tr 17 VD
Lực cản không khí tác dụng lên vật phụ thuộc vào vận tốc chuyển động theo công thức F = -k.v2 . Biết thứ nguyên của lực là M.L.T-2 . Xác định thứ nguyên và đơn vị của k trong hệ SI.
Phương pháp giải:
Thứ nguyên của một số đại lượng cơ bản

Các đơn vị cơ bản trong hệ SI

Lời giải chi tiết:
Vận tốc có thứ nguyên là L.T-1 nên v2 có thứ nguyên là L2 .T-2
=> Thứ nguyên của k là \(\left[ {\frac{{M.L.{T^{ - 2}}}}{{L^2.{T^{ - 2}}}}} \right] = \left[ M/L \right]\)
=> Đơn vị của k là kg/m
Câu hỏi tr 18
Với các dụng cụ là bình chia độ (ca đong) (Hình 3.1a) và cân (Hình 3.1b), đề xuất phương án đo khối lượng riêng của một quả cân trong phòng thí nghiệm.

Phương pháp giải:
Biểu thức tính khối lượng riêng \(\rho = \frac{m}{V}\)
Lời giải chi tiết:
Bước 1: Đặt quả cân lên cân để xác định khối lượng của quả cân
Bước 2: Đo thể tích của quả cân bằng cách đổ nước vào bình chia độ đến một vạch xác định, ghi lại kết quả đó. Sau đó thả quả cân vào bình chia độ, ghi lại kết quả
Vquả cân = Vnước + quả cân – Vnước
Bước 3: Áp dụng công thức tính khối lượng riêng \(\rho = \frac{m}{V}\) để tính khối lượng riêng của quả cân.
Câu hỏi tr 19 CH 5
Quan sát Hình 3.2 và phân tích các nguyên nhân gây ra sai số của phép đo trong các trường hợp được nêu.
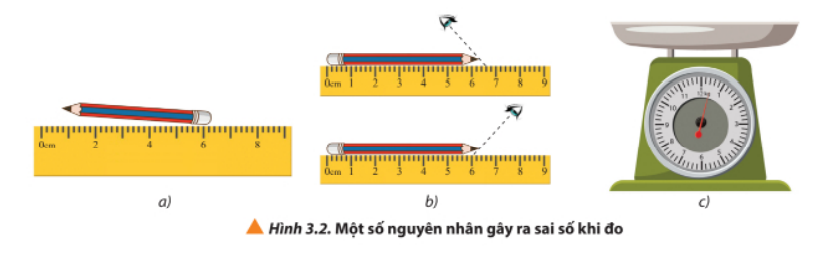
Phương pháp giải:
Quan sát hình và vận dụng kiến thức đã học trong KHTN 6
Lời giải chi tiết:
Nguyên nhân gây ra sai số là
+ Hình a: Đặt bút không đúng cách. Cần phải đặt bút song song với thước, một đầu của thước đặt vào vị trí số 0 của thước, đầu còn lại dừng ở vị trí nào của thước thì đó chính là số đo của thước
+ Hình b: Đặt mắt nhìn không đúng cách. Cần phải đặt mắt vuông góc với thước
+ Hình c: Cân điều chỉnh sai số. Cần điều chỉnh kim cân về vạch số 0 của cân.
Câu hỏi tr 19 CH 6
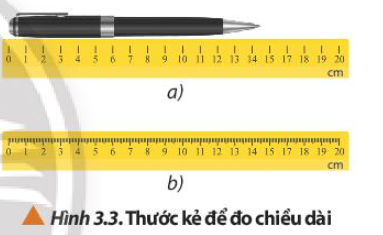
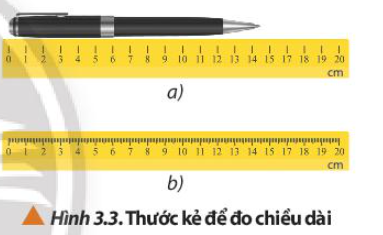
Quan sát Hình 3.3, em hãy xác định sai số dụng cụ của hai thước đo.
Phương pháp giải:
Sai số dụng cụ của thước xuất phát từ độ chia nhỏ nhất. Độ chia nhỏ nhất là khoảng cách gần nhất của hai vạch chia liên tiếp trên thước.
Lời giải chi tiết:
Hình a có độ chia nhỏ nhất là 1 cm nên sai số dụng cụ của thước là 1 cm
Hình b có độ chia nhỏ nhất là 1 mm nên sai số dụng cụ của thước là 1 mm.
Câu hỏi tr 19 CH 7
Đề xuất những phương án hạn chế sai số khi thực hiện phép đo.
Phương pháp giải:
Vận dụng kiến thức đã học
Lời giải chi tiết:
Phương án hạn chế sai số khi thực hiện phép đo là: Thường xuyên hiệu chỉnh dụng cụ đo, sử dụng thiết bị đo có độ chính xác cao.
Câu hỏi tr 20 LT
Để đo chiều dài của cây bút chì, em nên sử dụng loại thước nào trong Hình 3.3 để thu được kết quả chính xác hơn?
Phương pháp giải:
Vận dụng kiến thức đã học
Lời giải chi tiết:
Để đo chiều dài của cây bút chì, nên sử dụng thước trong Hình 3.3b vì thước này có sai số dụng cụ nhỏ hơn thước ở Hình 3.3a nên kết quả đo sẽ chính xác hơn.
Câu hỏi tr 20 VD
Một bạn chuẩn bị thực hiện đo khối lượng của một túi trái cây bằng cân như Hình 3.4. Hãy chỉ ra những sai số bạn có thể mắc phải. Từ đó, nêu cách hạn chế các sai số đó.

Phương pháp giải:
Quan sát hình vẽ và vận dụng kiến thức đã học
Lời giải chi tiết:
Những sai số bạn có thể mắc phải:
+ Sai số hệ thống: cân chưa được hiệu chỉnh về vị trí số 0
+ Sai số ngẫu nhiên: do các yếu tố bên ngoài như gió, bui, hoặc có thể đặt mắt không đúng
Cách hạn chế những sai sót:
+ Hiệu chỉnh cân về vị trí số 0, đặt đĩa cân cho thăng bằng
+ Khi đọc kết quả, mắt hướng về phía mặt cân và vuông góc
Câu hỏi tr 22 LT
Giả sử chiều dài của hai đoạn thẳng có giá trị đo được lần lượt là a = 51 ± 1 cm và b = 49 ± 1 cm. Trong các đại lượng được tính theo các cách sau đây, đại lượng nào có sai số tương đối lớn nhất:
A. a + b
B. a – b
C. a x b
D. \(\frac{a}{b}\)
Phương pháp giải:
Biểu thức tính sai số tương đối của phép đo: \(\delta x = \frac{{\Delta x}}{{\overline x }}\)
Trong đó Δx là sai số tuyệt đối
Sai số tương đối của một tích hoặc thương bằng tổng sai số tương đối của các thừa số
Sai số tuyệt đối của một tổng hay hiệu bằng tổng sai số tuyệt đối của các số hạng
Lời giải chi tiết:
A. a + b có F = a + b
=> \(\left[ {\frac{{M.L.{T^{ - 2}}}}{{{L^2}}}} \right] = \left[ {M.{L^{ - 1}}.{T^{ - 2}}} \right]\)
B. a – b có F = a – b
=> \(\delta F = \frac{{\Delta F}}{{\overline F }} = \frac{{\Delta a + \Delta b}}{{\overline a - \overline b }} = \frac{{1 + 1}}{{51 - 49}} = 1\)
C. a x b, có F = a x b
=> \(\delta F = \delta a + \delta b = \frac{{\Delta a}}{{\overline a }} + \frac{{\Delta b}}{{\overline b }} = \frac{1}{{51}} + \frac{1}{{49}} \approx 0,04\)
D. Có F = a/b
=> \(\delta F = \delta a + \delta b = \frac{{\Delta a}}{{\overline a }} + \frac{{\Delta b}}{{\overline b }} = \frac{1}{{51}} + \frac{1}{{49}} \approx 0,04\)
Chọn B.
Câu hỏi tr 22 VD
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.

Sai số tuyệt đối của phép đo: \(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = ?\)
Sai số tương đối của phép đo: \(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = ?\)
Kết quả phép đo: \(m = \overline m \pm \Delta m = ?\)
Phương pháp giải:
+ Giá trị trung bình: \(\overline m = \frac{{{m_1} + {m_2} + ... + {m_n}}}{n}\)
+ Sai số tuyệt đối ứng với mỗi lần đo: \(\Delta {m_i} = \left| {\overline m - {m_i}} \right|\)
+ Sai số tuyệt đối trung bình của n lần đo: \(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + ... + \Delta {m_n}}}{n}\)
Lời giải chi tiết:
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)
Câu hỏi tr 23 BT 1
Hãy phân tích thứ nguyên và thiết lập mối quan hệ giữa các đại lượng khối lượng riêng ρ, công suất P, áp suất p với đơn vị cơ bản
Phương pháp giải:
Thứ nguyên của một số đại lượng cơ bản

Các đơn vị cơ bản trong hệ SI

Lời giải chi tiết:
+ Biểu thức tính khối lượng riêng: \(\rho = \frac{m}{V}\)
Ta có thứ nguyên của khối lượng m là M, thứ nguyên của thể tích V là L3
=> Thứ nguyên của khối lượng riêng ρ là M.L-3
=> Đơn vị của khối lượng riêng là kg/m3
+ Biểu thức tính công suất là: \(P = \frac{A}{t} = \frac{{F.s}}{t}\)
F = m.a => F có thứ nguyên là M.L.T-2
=> Thứ nguyên của công suất là: \(\left[ {\frac{{M.L.{T^{ - 2}}.L}}{T}} \right] = \left[ {M.{L^2}.{T^{ - 3}}} \right]\)
=> Đơn vị của công suất là: kg.m2 /s3
+ Biểu thức tính áp suất: \(p = \frac{F}{S}\) ( F là lực tác dụng, S là diện tích tiếp xúc)
=> Thứ nguyên của áp suất là: \(\left[ {\frac{{M.L.{T^{ - 2}}}}{{{L^2}}}} \right] = \left[ {M.{L^{ - 1}}.{T^{ - 2}}} \right]\)
=> Đơn vị của áp suất là: kg.m/s2
Câu hỏi tr 23 BT 2
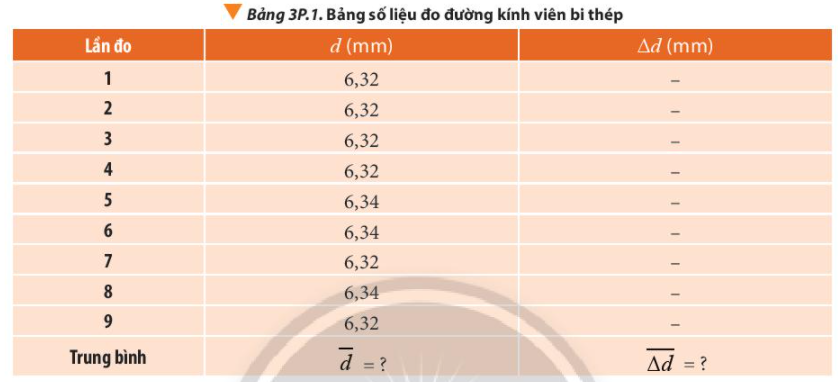
Bảng 3P.1 thể hiện kết quả đo đường kính của một viên bi thép bằng thước kẹp có sai số dụng cụ là 0,02 mm. Tính sai số tuyệt đối và biểu diễn kết quả phép đo có kèm theo sai số.
Phương pháp giải:
+ Giá trị trung bình: \(\overline d = \frac{{{d_1} + {d_2} + ... + {d_n}}}{n}\)
+ Sai số tuyệt đối ứng với mỗi lần đo: \(\Delta {d_i} = \left| {\overline d - {d_i}} \right|\)
+ Sai số tuyệt đối trung bình của n lần đo: \(\overline {\Delta d} = \frac{{\Delta {d_1} + \Delta {d_2} + ... + \Delta {d_n}}}{n}\)
+ Sai số tuyệt đối của phép đo: \(\Delta d = \overline {\Delta d} + \Delta {d_{dc}}\)
Lời giải chi tiết:
Giá trị trung bình của đường kính viên bi thép là:
\(\overline d = \frac{{{d_1} + {d_2} + ... + {d_9}}}{9} \approx 6,33(mm)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {d_1} = \left| {\overline d - {d_1}} \right| = \left| {6,33 - 6,32} \right| = 0,01(mm) = \Delta {d_2} = \Delta {d_3} = \Delta {d_4} = \Delta {d_7} = \Delta {d_9}\\\Delta {d_5} = \left| {\overline d - {d_5}} \right| = \left| {6,33 - 6,34} \right| = 0,01(mm) = \Delta {d_6} = \Delta {d_8}\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta d} = \frac{{\Delta {d_1} + \Delta {d_2} + ... + \Delta {d_9}}}{9} = 0,01(mm)\)
Sai số tuyệt đối của phép đo là:
\(\Delta d = \overline {\Delta d} + \Delta {d_{dc}} = 0,01 + 0,02 = 0,03(mm)\)
Luyện Bài Tập Trắc nghiệm Lí 10 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Bài 23. Định luật Hooke trang 140, 141, 142, 143 Vật Lí 10 Chân trời sáng tạo
- Bài 22. Biến dạng của vật rắn. Đặc tính của lò xo trang 136, 137, 138, 139 Vật Lí 10 Chân trời sáng tạo
- Bài 21. Động lực học của chuyển động tròn. Lực hướng tâm trang 131, 132, 133, 134 Vật Lí 10 Chân trời sáng tạo
- Bài 20. Động học của chuyển động tròn trang 126, 127, 128, 129, 130 Vật Lí 10 Chân trời sáng tạo
- Bài 19. Các loại va chạm trang 120, 121, 122, 123, 124, 125 Vật Lí 10 Chân trời sáng tạo
- Bài 23. Định luật Hooke trang 140, 141, 142, 143 Vật Lí 10 Chân trời sáng tạo
- Bài 22. Biến dạng của vật rắn. Đặc tính của lò xo trang 136, 137, 138, 139 Vật Lí 10 Chân trời sáng tạo
- Bài 21. Động lực học của chuyển động tròn. Lực hướng tâm trang 131, 132, 133, 134 Vật Lí 10 Chân trời sáng tạo
- Bài 20. Động học của chuyển động tròn trang 126, 127, 128, 129, 130 Vật Lí 10 Chân trời sáng tạo
- Bài 19. Các loại va chạm trang 120, 121, 122, 123, 124, 125 Vật Lí 10 Chân trời sáng tạo













Danh sách bình luận