Giải SBT Vật lý 11 Chủ đề 1. Dao động

Dao động điều hòa 1.1

Khẳng định nào dưới đây là đúng khi nói về chuyển động của một vật dao động điều hòa?

A. Khi vật ở vị trí biên, vận tốc của nó cực đại.

B. Khi vật ở vị trí cân bằng, gia tốc của nó cực đại.

C. Khi vật ở vị trí biên, gia tốc của nó bằng không.

D. Khi vật ở vị trí cân bằng, tốc độ của nó cực đại.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$

Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

Lời giải chi tiết:

Đáp án: D. Khi vật ở vị trí cân bằng, tốc độ của nó cực đại.

Dao động điều hòa 1.2

Khi nói về gia tốc của vật dao động điều hòa, phát biểu nào dưới đây là đúng?

A. Gia tốc của vật dao động điều hòa luôn không đổi theo thời gian.

B. Gia tốc của vật dao động điều hòa đạt cực đại khi vật ở vị trí biên.

C. Tỉ lệ nghịch với li độ.

D. Gia tốc của vật dao động điều hòa đạt cực đại khi vật ở vị trí cân bằng.

Phương pháp giải:

Vận dụng kiến thức đã học về đại lượng gia tốc của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$

Gia tốc của vật dao động điều hòa, biến thiên theo quy luật hàm số sin (cosin) cùng chu kì T của li độ.

Mối liên hệ giữa gia tốc và li độ: $a = - {\omega ^2}x$

Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

Lời giải chi tiết:

Đáp án: B. Gia tốc của vật dao động điều hòa đạt cực đại khi vật ở vị trí biên.

Dao động điều hòa 1.3

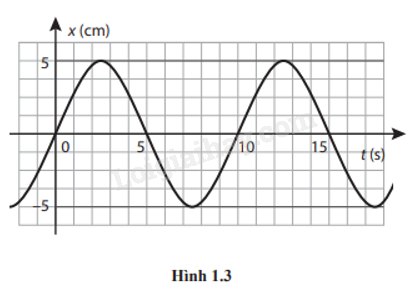
Cho đồ thị li độ - thời gian của một vật dao động điều hòa như Hình 1.3. Thông tin nào dưới đây là đúng?

A. Biên độ của dao động là 10 cm.

B. Tần số của dao động là 10 Hz.

C. Chu kì của dao động là 10 s.

D. Tần số góc của dao động là 0,1 rad/s.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$

- Đồ thị dao động điều hòa.

+ Biên độ của dao động: độ lớn cực đại của li độ theo trục 0x.

+ Chu kì của dao động: Khoảng thời gian vật thực hiện một dao động.

+ Tần số dao động: $f = \frac{1}{T}$Số dao động vật thực hiện được trong một giây.

+ Tần số góc của dao động: $\omega = \frac{{2\pi }}{T} = 2\pi f$

Lời giải chi tiết:

Biên độ của dao động là 5 cm.

Chu kì của dao động là 10 s.

Tần số của dao động là $f = \frac{1}{T} = \frac{1}{{10}} = 0,1{\rm{ Hz}}$

Tần số góc của dao động $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{10}} = 0,63{\rm{ rad/s}}$

Đáp án: C. Chu kì của dao động là 10 s.

Dao động điều hòa 1.4

Một vật dao động điều hòa với phương trình x=4cos5t (cm) (t tính bằng s). Tốc độ của vật khi đi qua vị trí cân bằng là

A. 50 cm/s

B. 20 cm/s.

C. 100 cm/s.

D. 80 cm/s.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$với:

Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

Lời giải chi tiết:

Phương trình li độ của vật là: x=4cos5t.

Khi vật đi qua VTCB,

$ \Rightarrow v = {v_{max}} = \pm \omega A = \pm 5.4 = \pm 20{\rm{ cm/s}}$

Tốc độ là độ lớn của vận tốc.

Vậy tốc độ của vật là 20 cm/s.

Đáp án: B. 20 cm/s.

Dao động điều hòa 1.5

Sau khi chạy một quãng đường ngắn, nhịp tim của một bạn học sinh là 96 nhịp mỗi phút. Tần số đập của tim bạn học sinh đó là:

A. 96 Hz.

B. 1,6 Hz.

C. 0,67 Hz.

D. 0,010 Hz.

Phương pháp giải:

Áp dụng kiến thức về tần số.

Tần số f là số dao động vật thực hiện được trong một giây.

Lời giải chi tiết:

Tần số đập của tim bạn học sinh đó là:

$f = \frac{{9,6}}{{60}} = 1,6{\rm{ Hz}}$

Đáp án: B. 1,6 Hz.

Dao động điều hòa 1.6

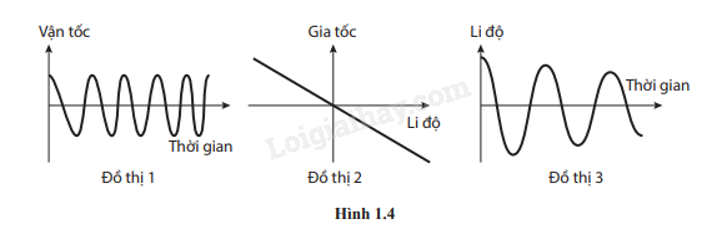
Trong ba đồ thị ở Hình 1.4, đồ thị nào mô tả vật dao động điều hòa? Gỉai thích vì sao.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$

- Đồ thị dao động điều hoà.

Lời giải chi tiết:

Đồ thị 1 không mô tả vật dao động điều hòa vì dựa vào đồ thị, ta thấy chu kì giảm dần theo thời gian.

Đồ thị 2 mô tả vật dao động điều hòa vì dựa vào đồ thị, ta thấy gia tốc a tỉ lệ thuận với li độ -x.

Đồ thị 3 không mô tả vật dao động điều hòa vì dựa vào đồ thị, ta thấy biên độ thay đổi theo thời gian.

Đáp án: Đồ thị 2

Dao động điều hòa 1.7

Âm thoa y tế như trong Hình 1.5 được sử dụng để phát hiện triệu chứng giảm sự nhạy cảm với các rung động – một biểu hiện của chứng rối loạn thần kinh. Âm thoa này có tần số 128 Hz. Chu kì dao động của âm thoa là bao nhiêu.

Phương pháp giải:

Vận dụng kiến thức về tần số và chu kì của dao động điều hòa.

Tần số f là số dao động vật thực hiện được trong một giây.

Chu kì T là khoảng thời gian để vật thực hiện một dao động. $T = \frac{1}{f}$

Lời giải chi tiết:

Chu kì dao động của âm thoa là:

$T = \frac{1}{f} = \frac{1}{{128}} = 7,{8125.10^{ - 3}}{\rm{ s = 7,8125 ms}}$

Đáp án: 7,8125 ms

Dao động điều hòa 1.8

Một nguyên tử trong tinh thể dao động điều hòa với tần số 1,0.10¹⁴ Hz. Biên độ dao động của nguyên tử đó là 2,0.10^-12 m. Xác định:

a) Tốc độ cực đại của nguyên tử.

b) Gia tốc cực đại của nguyên tử.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$

Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

Tốc độ là độ lớn của vận tốc.

Lời giải chi tiết:

Nguyên tử đó dao động với tần số góc:

$\omega = 2\pi f = 2\pi {.10^{14}}{\rm{ rad/s}}$

a) Tốc độ dao động cực đại của nguyên tử:

${v_{max}} = \omega A = 2\pi {.10^{14}}{.2.10^{ - 12}} = 4\pi {10^{ - 12}} = 400\pi {\rm{ m/s}}$

b) Gia tốc cực đại của nguyên tử:

${a_{max}} = {\omega ^2}A = {\left( {2\pi {{.10}^{14}}} \right)^2}{.2.10^{ - 12}} = 8{\pi ^2}{10^{16}}{\rm{ m/}}{{\rm{s}}^2}$

Dao động điều hòa 1.9

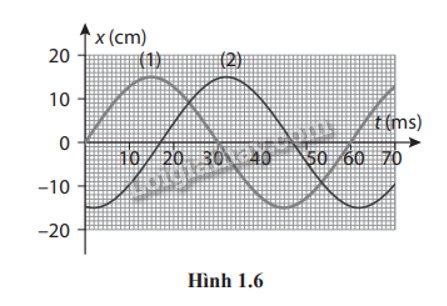
Cho hai dao động điều hòa (1) và (2) có đồ thị li độ - thời gian như Hình 1.6. Xác định:

a) Biên độ, chu kì, tẩn số của mỗi dao động.

b) Độ lệch pha của hai dao động tính theo đơn vị độ và rad.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$

- Đồ thị dao động điều hoà.

- Độ lệch pha của hai dao động cùng tần số.

Lời giải chi tiết:

a) Từ đồ thị ta thấy:

Xét dao động điều hòa (1)

- Biên độ dao động là giá trị lớn nhất của li độ: A = 15 cm

- Chu kì dao động của vật: T = 60 ms

- Tần số dao động của vật: $f = \frac{1}{T} = \frac{1}{{{{60.10}^{ - 3}}}} = 16,7{\rm{ Hz}}$

Xét dao động điều hòa (2)

- Biên độ dao động là giá trị lớn nhất của li độ: A = 15 cm

- Chu kì dao động của vật: T = 60 ms

- Tần số dao động của vật: $f = \frac{1}{T} = \frac{1}{{{{60.10}^{ - 3}}}} = 16,7{\rm{ Hz}}$

b) Hai vật dao động cùng chu kì T.

Từ đồ thị, ta thấy độ lệch thời gian của hai dao động khi cùng một trạng thái là:

$\Delta t = 17{\rm{ ms}}$

Độ lệch pha của hai dao động là:

$\Delta \varphi = \frac{{\Delta t}}{T} = \frac{{17}}{{60}}$ dao động

Độ lệch pha tính theo đơn vị độ: $\Delta \varphi = \frac{{17}}{{60}}{.360^o} = {102^o}$

Độ lệch pha tính theo đơn vị rad: $\Delta \varphi = \frac{{17}}{{60}}.2\pi = \frac{{17\pi }}{{30}}{\rm{ rad}}$

Dao động điều hòa 1.10

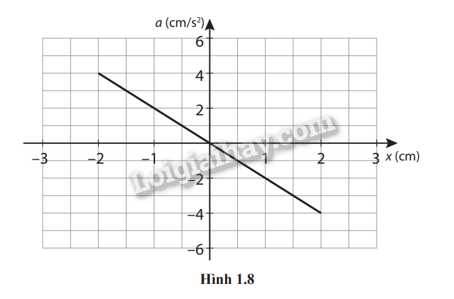
Bố trí thí nghiệm như trong Hình 1.7. Vật có khối lượng m được gắn chặt vào một đầu thước kẻ và cho dao động điều hòa tự do dưới tác dụng của cú gảy ban đầu. Một máy đo gia tốc được gắn với vật giúp ta xác định được gia tốc của nó ở các vị trí khác nhau. Đồ thị biểu diễn sự phụ thuộc của gia tốc vào li độ được cho như trong Hình 1.8.

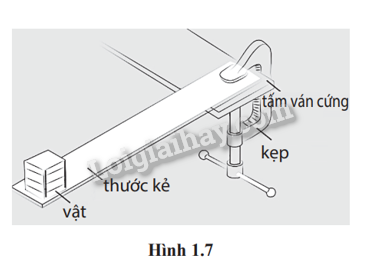
a) Giải thích tại sao đồ thị có dạng đường thẳng với độ dốc âm.

b) Từ đồ thị xác định biên độ và gia tốc cực đại của vật.

c) Xác định tần số góc và chu kì dao động của vật.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà.

+ Mối liên hệ giữa gia tốc và li độ: $a = - {\omega ^2}x$

+ Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

+ Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

- Đồ thị dao động điều hòa.

+ Biên độ của dao động A: độ lớn cực đại của li độ x

+ Chu kì của dao động $T = \frac{{2\pi }}{\omega }$

+ Tần số góc của dao động $\omega $

Lời giải chi tiết:

a) Đồ thị biểu diễn mối liên hệ giữa gia tốc và li độ bằng phương trình $a = - {\omega ^2}x$với $\omega $không đổi. Nên độ dốc của đồ thị là: $ - {\omega ^2} < 0$

Vì vậy, đồ thị có dạng đường thẳng với độ dốc âm.

b) Từ đồ thị, dễ thấy biên độ của vật là A = 2 cm, gia tốc cực đại của vật là a = 4 cm/s².

c) Tần số góc của vật là :

${\omega ^2} = \frac{{{a_{max}}}}{x} = \frac{4}{2} = 2{\rm{ }}$

$ \Rightarrow \omega = \sqrt 2 {\rm{ rad/s}}$

Chu kì dao động của vật là :

$T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\sqrt 2 }} = \pi \sqrt 2 {\rm{ s}}$

Dao động điều hòa 1.11

Một vật dao động điều hòa với tần số 60,0 Hz và biên độ 2,50 cm. Tính tốc độ của vật khi nó ở li độ 0,800 cm.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$với:

+ x là li độ dao động.

+ A là biên độ dao động.

+ Tần số góc của dao động là $\omega = 2\pi f$

+ $\left( {\omega t + \varphi } \right)$ là pha của dao động ở thời điểm t.

+ $\varphi $ là pha ban đầu.

- Phương trình vận tốc của vật: $v = \omega A\sin \left( {\omega t + \varphi } \right)$

- Phương trình vuông pha giữa li độ và vận tốc: $\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1$

Lời giải chi tiết:

Tần số góc của vật là : $\omega = 2\pi f = 2\pi .60 = 120\pi {\rm{ rad/s}}$

Phương trình vuông pha giữa li độ và vận tốc: $\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1$

Thay x = 0,8 cm.

$ \Rightarrow \frac{{0,{8^2}}}{{2,{5^2}}} + \frac{{{v^2}}}{{{{\left( {120\pi .2,5} \right)}^2}}} = 1$

$ \Rightarrow v = \pm 120\pi .2,5\sqrt {1 - \frac{{0,{8^2}}}{{2,{5^2}}}} = \pm 892,92{\rm{ cm/s}}$

Mà tốc độ là độ lớn của vận tốc.

Vậy tốc độ của vật khi nó ở li độ 0,800 cm là 892,92 cm/s

Dao động điều hòa 1.12

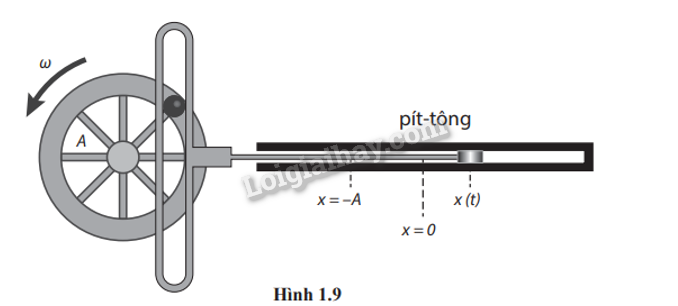
Bánh xe trong mô hình động cơ đơn giản ở Hình 1.9 có bán kính A = 0,250 m. Khi pít-tông dao động điều hòa theo phương ngang với biên độ bằng A và tần số góc $\omega $ = 12,0 rad/s thì bánh xe quay đều liên tục với tốc độ góc $\omega $. Tại thời điểm t = 0, pít-tông đang ở vị trí x = A.

a) Viết các phương trình li độ, vận tốc và gia tốc của pít-tông.

b) Xác định vị trí, vận tốc và gia tốc của pít-tông tại thời điểm t = 1,15 s.

c) Tính quãng đường pít-tông di chuyển được trong thời gian bánh xe quay 120 vòng.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà.

+ Phương trình li độ: $x = A\cos \left( {\omega t + \varphi } \right)$

+ Phương trình vận tốc: $v = \omega A\sin \left( {\omega t + \varphi } \right)$

+ Phương trình gia tốc: $a = - {\omega ^2}A\cos \left( {\omega t + \varphi } \right)$

+ A là biên độ dao động.

+ $\omega $là tần số góc của dao động.

+ $\left( {\omega t + \varphi } \right)$là pha của dao động ở thời điểm t.

+ $\varphi $là pha ban đầu.

- Quãng đường vật đi hết một chu kì là S = 4A.

Lời giải chi tiết:

a) Pít-tông

Phương trình li độ của pít-tông có dạng : $x = A\cos \left( {\omega t + \varphi } \right)$

Phương trình vận tốc của pít-tông có dạng : $v = \omega A\sin \left( {\omega t + \varphi } \right)$

Phương trình gia tốc của pít-tông có dạng : $a = - {\omega ^2}A\cos \left( {\omega t + \varphi } \right)$

Khi t = 0, pít-tông đang ở vị trí A => pha ban đầu $\varphi = 0$

Từ đề bài, biên độ A = 0,25 m, tần số góc $\omega = {\rm{12 rad/s}}$

=> Phương trình li độ: $x = 0,25\cos 12t{\rm{ }}\left( m \right)$

=> Phương trình vận tốc: $v = 3\sin 12t{\rm{ }}\left( {{\rm{m/s}}} \right)$

=> Phương trình gia tốc: $a = - 36\cos 12t{\rm{ }}\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)$

b) Thời điểm t = 1,15 s.

Pít-tông ở:

- Vị trí: $x = 0,25\cos \left( {12.1,15} \right){\rm{ = 0,0827 m = 2,27 cm}}$

- Vận tốc: $v = 3\sin \left( {12.1,15} \right){\rm{ = 2,83 m/s}}$

- Gia tốc: $x = - 36\cos \left( {12.1,15} \right){\rm{ = }} - {\rm{11,91 m/}}{{\rm{s}}^2}$

c) Khi bánh xe quay 120 vòng, pít-tông thực hiện được 120 chu kì dao động. Trong mỗi chu kì, pít-tông di chuyển quãng đường bằng 4A. Do đó, quãng đường pít-tông di chuyển trong 120 chu kì là:

s = 120.4A = 120 m.

Dao động điều hòa 1.13

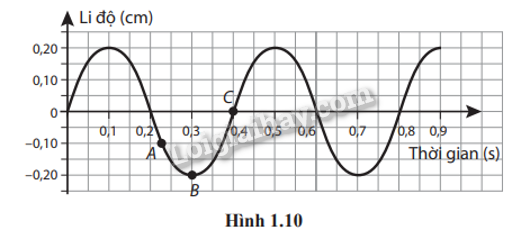
Cho đồ thị li độ - thời gian của một vật dao động điều hòa như Hình 1.10. Xác định:

a) Biên độ, chu kì, tần số và tần số góc của dao động.

b) Vận tốc và gia tốc của vật tại các điểm A, B, C.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$

+ Mối liên hệ giữa gia tốc và li độ: $a = - {\omega ^2}x$

+ Tính chất vuông pha giữa các đại lượng: $v = \pm \omega \sqrt {{A^2} - {x^2}} $

+ Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

+ Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

+ A là biên độ dao động.

+ $\omega $là tần số góc của dao động.

+ $\left( {\omega t + \varphi } \right)$ là pha của dao động ở thời điểm t.

+ $\varphi $là pha ban đầu.

- Đồ thị dao động điều hoà.

Lời giải chi tiết:

a) Từ hình vẽ, vật dao động có:

Biên độ A = 0,2 cm;

Chu kì T = 0,4 s;

Tần số $T = \frac{1}{f} = \frac{1}{{0,4}} = 2,5{\rm{ Hz;}}$

Tần số góc $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi {\rm{ rad/s;}}$

b) Xác định vận tốc, gia tốc của vật tại các điểm

Tại điểm A:

Li độ x = -0,1 cm

=> Gia tốc $a = - {\omega ^2}x = - {\left( {5\pi } \right)^2}\left( { - 0,1} \right) = 24,67{\rm{ cm/}}{{\rm{s}}^2}$

Vận tốc: $v = \pm \omega \sqrt {{A^2} - {x^2}} = \pm 5\pi \sqrt {0,{2^2} - {{\left( { - 0,1} \right)}^2}} = \pm 2,72{\rm{ cm/s}}$

Theo đồ thị, vật đang di chuyển theo chiều âm của trục tọa độ => v < 0

=> Vận tốc: v = -2,72 cm/s

Tại điểm B:

Li độ x = -A = -0,2 cm

=> Vận tốc v = 0

=> Gia tốc $a = - {\omega ^2}x = - {\left( {5\pi } \right)^2}\left( { - 0,2} \right) = 249,35{\rm{ cm/}}{{\rm{s}}^2}$

Tại điểm C:

Li độ x = 0, vật đang di chuyển theo chiều dương của trục tọa độ.

=> Vận tốc v > 0; $v = \omega A = 5\pi .0,2 = \pi {\rm{ cm/s}}$

=> Gia tốc a = 0.

Dao động điều hòa 1.14

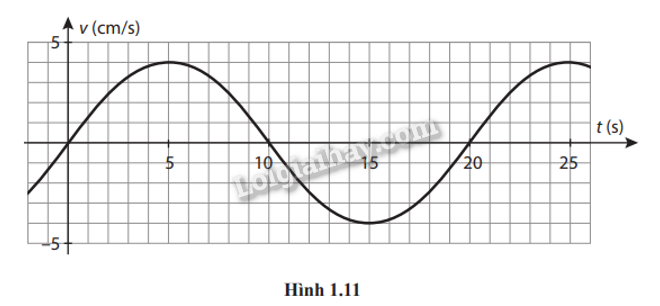
Cho đồ thị vận tốc – thời gian của một vật dao động điều hòa như Hình 1.11. Xác định:

a) Biên độ và tần số của dao động.

b) Vị trí và gia tốc của vật tại các thời điểm t = 10,0 s và t = 15,0 s.

Phương pháp giải:

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: $x = A\cos \left( {\omega t + \varphi } \right)$

+ Mối liên hệ giữa gia tốc và li độ: $a = - {\omega ^2}x$

+ Tính chất vuông pha giữa các đại lượng: $v = \pm \omega \sqrt {{A^2} - {x^2}} $

+ Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

+ Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

+ A là biên độ dao động.

+ $\omega $là tần số góc của dao động.

+ $\left( {\omega t + \varphi } \right)$ là pha của dao động ở thời điểm t.

+ $\varphi $là pha ban đầu.

- Đồ thị dao động điều hoà.

Lời giải chi tiết:

a) Từ đồ thị, vật có chu kì T = 20 s, vận tốc v_max = 4 cm/s

=> Tần số góc của vật: $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{20}} = 0,1\pi {\rm{ rad/s}}$

=> Biên độ của vật: $A = \frac{{{v_{max}}}}{\omega } = \frac{4}{{0,1\pi }} = 12,73{\rm{ = cm}}$

b) Tại thời điểm t = 10 s, từ đồ thị, ta có v = 0, vật chuẩn bị có vận tốc âm.

=> Vật đang ở vị trí biên dương.

=> Do đó, vật ở vị trí x = A = 12,73 cm ; gia tốc $a = - {\omega ^2}A = - 1,25{\rm{ cm/}}{{\rm{s}}^2}$

Tại thời điểm t = 15 s, từ đồ thị, ta có v = -4 cm/s = v_max nên vật đang ở VTCB, x = 0, a = 0.

Một số dao động điều hòa thường gặp 1.15

Con lắc lò xo gồm lò xo khối lượng không đáng kể, một đầu cố định và đầu kia gắn với một viên bi nhỏ. Con lắc này đang dao động điều hoà theo phương nằm ngang. Lực đàn hồi của lò xo tác dụng lên viên bi luôn hướng

A. theo chiều chuyển động của viên bi.

B. về vị trí cân bằng của viên bi.

C. ngược chiều chuyển động của viên bi.

D. về vị trí biên.

Phương pháp giải:

Vận dụng kiến thức đã học về chu kì dao động của con lắc lò xo: $T = 2\pi \sqrt {\frac{m}{k}} $

Lời giải chi tiết:

Đáp án: B. về vị trí cân bằng của viên bi.

Một số dao động điều hòa thường gặp 1.16

Tại một nơi xác định, chu kì của con lắc đơn tỉ lệ thuận với

A. căn bậc hai gia tốc trọng trường.

B. gia tốc trọng trường.

C. căn bậc hai chiều dài con lắc.

D. chiều dài con lắc.

Phương pháp giải:

Vận dụng kiến thức đã học về chu kì dao động của con lắc đơn: $T = 2\pi \sqrt {\frac{l}{g}} $

Lời giải chi tiết:

Đáp án: C. căn bậc hai chiều dài con lắc.

Một số dao động điều hòa thường gặp 1.17

Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k không đổi, dao động điều hoà. Nếu khối lượng m = 200 g thì chu kì dao động của con lắc là 2 s. Để chu kì con lắc là 1 s thì khối lượng m bằng

A. 200 g.

B. 100 g.

C. 50 g.

D. 800 g.

Phương pháp giải:

Vận dụng kiến thức đã học về chu kì dao động của con lắc lò xo: $T = 2\pi \sqrt {\frac{m}{k}} $

Lời giải chi tiết:

$\begin{array}{l}\frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{m_1}}}{{{m_2}}}} \\ \Rightarrow {m_2} = {m_1}{\left( {\frac{{{T_1}}}{{{T_2}}}} \right)^2} = 200.\frac{{{2^2}}}{{{1^2}}} = 800{\rm{ g}}\end{array}$

Một số dao động điều hòa thường gặp 1.18

Trong thực hành, để đo gia tốc trọng trường, một học sinh dùng con lắc đơn có chiều dài dây treo 80,00 cm. Khi cho con lắc dao động điều hoà, học sinh này thấy con lắc thực hiện được 20,00 dao động trong thời gian 36,00 s. Theo kết quả thí nghiệm trên, gia tốc trọng trường tại nơi học sinh làm thí nghiệm bằng

A. 9,847 cm/s².

B. 9,874 cm/s².

C. 9,748 cm/s².

D. 9,783 cm/s².

Phương pháp giải:

Vận dụng kiến thức đã học về chu kì dao động của con lắc đơn: $T = 2\pi \sqrt {\frac{l}{g}} $

Lời giải chi tiết:

Chu kì dao động của con lắc đơn này là:

$T = \frac{{36}}{{20}} = 1,8{\rm{ s}}$

Gia tốc trọng trường tại nơi con lắc đơn dao động là:

$g = \frac{{4{\pi ^2}l}}{{{T^2}}} = \frac{{4{\pi ^2}.0,8}}{{1,{8^2}}} = 9,748{\rm{ cm/}}{{\rm{s}}^2}$

Đáp án: C. 9,748 cm/s².

Một số dao động điều hòa thường gặp 1.19

Thú nhún lò xo (Hình 1.12) là một loại đồ chơi của các em nhỏ. So sánh chu kì dao động của thú nhún nếu hai em bé có khối lượng khác nhau m₁ > m₂lần lượt ngồi lên con thú nhún này.

Phương pháp giải:

Vận dụng kiến thức đã học về chu kì dao động của con lắc lò xo: $T = 2\pi \sqrt {\frac{m}{k}} $

Lời giải chi tiết:

Ta có: $T = 2\pi \sqrt {\frac{m}{k}} $

Theo đề bài m₁ > m₂

=> T₁ > T₂

Vì vậy, em bé có khối lượng lớn hơn ngồi lên thú nhún sẽ làm thú nhún dao động với chu kì dài hơn.

Một số dao động điều hòa thường gặp 1.20

Các nhạc sĩ sử dụng máy gõ nhịp như trong Hình 1.13 để rèn luyện khả năng chơi nhạc theo một nhịp độ nhất định. Thanh gõ nhịp của máy có thể coi gần đúng là một con lắc đơn. Nếu muốn máy gõ nhịp nhanh hơn thì cần điều chỉnh đầu trượt của thanh lên cao hay xuống thấp? Giải thích vì sao.

Phương pháp giải:

Vận dụng kiến thức đã học về chu kì dao động của con lắc đơn: $T = 2\pi \sqrt {\frac{l}{g}} $

Lời giải chi tiết:

Theo đề bài, coi gần đúng thanh gõ nhịp là con lắc đơn nên chu kì của thanh gõ nhip được tính bằng công thức: $T = 2\pi \sqrt {\frac{l}{g}} $

Để máy gõ nhịp nhanh hơn => T nhỏ đi => l giảm xuống => Cần điều chỉnh đầu trượt của thanh xuống thấp.

Như vậy, để mãy gõ nhịp nhanh hơn thì cần điều chỉnh đầu trượt của thanh xuống thấp.

Một số dao động điều hòa thường gặp 1.21

Một con lắc lò xo treo thẳng đứng ở nơi có gia tốc trọng trường 9,8 m/s². Khi vật ở vị trí cân bằng, lò xo giãn một đoạn 2,5 cm. Tính chu kì dao động của con lắc lò xo này.

Phương pháp giải:

Vận dụng kiến thức đã học về chu kì dao động và định luật II Newton.

- Chu kì dao động của con lắc lò xo: $T = 2\pi \sqrt {\frac{m}{k}} $

- Chu kì dao động của con lắc đơn: $T = 2\pi \sqrt {\frac{l}{g}} $

Lời giải chi tiết:

Các lực tác dụng lên con lắc lò xo: ${\vec F_{dh}};\vec P.$

Theo định luật II Newton, ta có:

${\vec F_{dh}} + \vec P = m\vec a$

Ở VTCB, gia tốc của vật bằng 0, lực đàn hồi ngược chiều với trọng lực

$ = > {\rm{ }}P = {F_{dh}} < = > {\rm{ }}mg{\rm{ }} = k\left| {\Delta {l_0}} \right| < = > \frac{m}{k} = \frac{{\left| {\Delta {l_0}} \right|}}{g} = \frac{{2,{{5.10}^{ - 2}}}}{{9,8}} = 2,{55.10^{ - 3}}$

Chu kì của con lắc lò xo là: $T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {2,{{55.10}^{ - 3}}} = 0,32{\rm{ s}}$

Một số dao động điều hòa thường gặp 1.22

Một con lắc lò xo gồm vật có khối lượng 0,500 kg mắc với lò xo nhẹ có độ cứng 70,0 N/m. Con lắc dao động với biên độ 4,00 cm. Tính tốc độ của vật khi qua vị trí cân bằng.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa:

- Tần số góc : $\omega = \sqrt {\frac{k}{m}} $

- Khi vật đi qua VTCB, tốc độ của của vật : $\left| v \right| = {v_{max}}{\rm{ = }}\omega A$

Lời giải chi tiết:

Tần số góc của con lắc lò xo này là:

$\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{70}}{{0,5}}} = 11,83{\rm{ rad/s}}$

Tốc độ của vật khi qua VTCB là:

${v_{max}}{\rm{ = }}\omega A = 11,83.4 = 47,3{\rm{ cm/s}}$

Một số dao động điều hòa thường gặp 1.23

Một con lắc đơn có chiều dài dây treo 1,2 m dao động điều hoà với biên độ 5,0 cm tại nơi có gia tốc trọng trường 9,8 m/s² . Tính tốc độ và gia tốc của con lắc khi qua vị trí có li độ 2,5 cm.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa:

- Tần số góc : $\omega = \sqrt {\frac{k}{m}} $

- Mối liên hệ giữa gia tốc và li độ : ${\rm{a = - }}{\omega ^2}x$

- Mối liên hệ giữa tốc độ, li độ, biên độ và tần số góc: $\left| v \right| = \sqrt {{\omega ^2}\left( {{A^2} - {x^2}} \right)} $

Lời giải chi tiết:

Tần số góc của con lắc đơn này là:

$\omega = \sqrt {\frac{g}{l}} = \sqrt {\frac{{9,8}}{{1,2}}} = 2,9{\rm{ rad/s}}$

Khi vật có li độ 2,5 cm thì gia tốc ${\rm{a = - }}{\omega ^2}x = - 2,{9^2}.2,5 = - 21{\rm{ cm/}}{{\rm{s}}^2}$

Tốc độ của vật khi đó là:

$\left| v \right| = \sqrt {{\omega ^2}\left( {{A^2} - {x^2}} \right)} = \sqrt {2,{9^2}\left( {{5^2} - 2,{5^2}} \right)} = 13{\rm{ cm/s}}$

Một số dao động điều hòa thường gặp 1.24

Trong các máy đo gia tốc thường có một con lắc lò xo gồm vật có khối lượng m, gắn với một cặp lò xo. Vật sẽ dao động điều hoà khi máy chuyển động có gia tốc. Một máy đo gia tốc gồm vật khối lượng 0,080 kg, gắn với cặp lò xo có độ cứng 4,0.10³ N/m. Biên độ của vật khi dao động là 2,0 cm. Xác định:

a) Chu kì dao động của con lắc lò xo.

b) Gia tốc cực đại của vật.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa:

- Chu kì dao động : $T = 2\pi \sqrt {\frac{m}{k}} $

- Tần số góc : $\omega = \sqrt {\frac{k}{m}} $

- Gia tốc cực đại của vật : ${a_{max}}{\rm{ = }}{\omega ^2}A$

Lời giải chi tiết:

a) Chu kì dao động của con lắc lò xo là:

$T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{0,08}}{{{{4.10}^3}}}} = 0,028{\rm{ s}}$

b) Gia tốc cực đại của vật là:

${a_{max}}{\rm{ = }}{\omega ^2}A = \frac{k}{m}.A = \frac{{4,{{10}^3}}}{{0,08}}.2 = {10^5}{\rm{ cm/}}{{\rm{s}}^2}$

Một số dao động điều hòa thường gặp 1.25

Một vật có khối lượng 0,250 kg được gắn vào lò xo nhẹ để dao động với biên độ 0,125 m trên mặt bàn nằm ngang không ma sát. Khi vật đi qua vị trí cân bằng, tốc độ của nó là 3,00 m/s.

a) Tìm độ cứng của lò xo.

b) Tìm tốc độ của vật khi nó ở vị trí có li độ x = A/2.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa:

- Tần số góc : $\omega = \sqrt {\frac{k}{m}} $

- Tốc độ của vật: $\left| v \right| = \sqrt {{\omega ^2}\left( {{A^2} - {x^2}} \right)} $

- Tại x = 0, tốc độ của vật: ${v_{max}}{\rm{ = }}\omega A$

Lời giải chi tiết:

a) Khi đi qua VTCB, vật có tốc độ là lớn nhất: $\left| v \right| = {v_{max}}{\rm{ = }}\omega A = 3{\rm{ m/s}}$

Tần số góc của vật là : $\omega = \frac{{{v_{max}}}}{A}{\rm{ = }}\frac{3}{{0,125}}{\rm{ = 24 rad/s}}$

Độ cứng của lò xo là: $k = m{\omega ^2}{\rm{ = 0,25}}{\rm{.2}}{{\rm{4}}^2}{\rm{ = 144 N/m}}$

b) Tại vị trí có li độ x = A/2=0,0625 m, tốc độ của vật là:

$\left| v \right| = \sqrt {{\omega ^2}\left( {{A^2} - {x^2}} \right)} = \sqrt {{{24}^2}\left( {0,{{125}^2} - 0,{{0625}^2}} \right)} {\rm{ = 2,6 m/s}}$

Một số dao động điều hòa thường gặp 1.26

Một con lắc đơn gồm vật nhỏ treo vào sợi dây có chiều dài l và dao động điều hoà tại nơi có gia tốc trọng trường 9,81 m/s² . Đồ thị li độ – thời gian của vật được cho trong Hình 1.14. Xác định:

a) Biên độ và chu kì của dao động.

b) Chiều dài l của dây treo.

c) Vận tốc của vật tại thời điểm t = 2,00 s.

d) Gia tốc của vật tại thời điểm t = 3,00 s.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa:

- Chu kì dao động của con lắc đơn: $T = 2\pi \sqrt {\frac{l}{g}} $

- Tần số góc : $\omega = \frac{{2\pi }}{T}$

- Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

- Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

Lời giải chi tiết:

a) Từ đồ thị, dễ thấy biên độ A = 2 cm và chu kì T = 4 s.

b) Có $T = 2\pi \sqrt {\frac{l}{g}} $

$ \Rightarrow l = \frac{{g{T^2}}}{{4{\pi ^2}}} = \frac{{9,{{81.4}^2}}}{{4{\pi ^2}}} = 3,98{\rm{ m}}$

Vậy chiều dài l của dây treo là 3,98 m.

c) Tốc độ góc của vật là : $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{4} = \frac{\pi }{2}{\rm{ rad/s}}$

Tại t = 2 s; vật ở VTCB, chiều chuyển động ngược chiều dương.

Vận tốc của vật: $v = - {v_{max}} = - \omega A = - \frac{\pi }{2}.2 = - \pi {\rm{ cm/s}}$

d) Tại t = 3 s; vật ở vị trí biên âm.

Gia tốc của vật $a = {a_{max}} = {\omega ^2}A = {\left( {\frac{\pi }{2}} \right)^2}.2 = 4,93{\rm{ cm/}}{{\rm{s}}^2}$

Một số dao động điều hòa thường gặp 1.27

Một con lắc lò xo treo thẳng đứng gồm vật có khối lượng m = 0,20 kg gắn vào lò xo nhẹ có độ cứng k. Trong quá trình vật dao động với chu kì 0,40 s, chiều dài của lò xo thay đổi trong khoảng l_min = 0,20 m đến l_max = 0,24 m. Gia tốc trọng trường tại nơi treo con lắc là 9,8 m/s² . Xác định:

a) Biên độ của dao động.

b) Tốc độ cực đại và gia tốc cực đại của vật.

c) Chiều dài của lò xo khi chưa biến dạng.

d) Độ lớn lực đàn hồi của lò xo khi nó có chiều dài lớn nhất.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa:

- Biên độ dao động của con lắc lò xo thẳng đứng là : $A = \frac{{{l_{max}} - {l_{\min }}}}{2}$

- Độ dãn của lò xo khi vật ở VTCB là: $\Delta {l_0} = \frac{{mg}}{k}$

- Chu kì dao động: $T = 2\pi \sqrt {\frac{m}{k}} $

- Tần số góc : $\omega = \frac{{2\pi }}{T}$

- Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

- Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

- Độ lớn lực đàn hồi: ${F_{dh}} = k\Delta l$

Lời giải chi tiết:

a) Biên độ của dao động là : $A = \frac{{{l_{max}} - {l_{\min }}}}{2} = \frac{{0,24 - 0,20}}{2} = 0,02{\rm{ m}}$

b) Tần số góc của vật là: $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 15,7{\rm{ rad/s}}$

Tốc độ cực đại của vật là: ${v_{max}} = \omega A = 15,7.0,02 = 0,3{\rm{ m/s}}$

Gia tốc cực đại của vật là: ${a_{max}} = {\omega ^2}A = 15,{7^2}.0,02 = 5{\rm{ m/}}{{\rm{s}}^2}$

c) Độ dãn của lò xo khi vật ở VTCB là: $\Delta {l_0} = \frac{{mg}}{k} = \frac{g}{{{\omega ^2}}} = \frac{{9,8}}{{15,{7^2}}} = 0,04{\rm{ m}}$

Chiều dài của lò xo khi chưa biến dạng là: ${l_0} = {l_{max}} - A - \Delta {l_0} = 0,24 - 0,02 - 0,04 = 0,18{\rm{ m}}$

d) Khi lò xo có chiều dài lớn nhất, độ biến dạng của nó là:

$\Delta {l_{max}} = A + \Delta {l_0} = 0,02 + 0,04 = 0,06{\rm{ m}}$

Độ cứng k của lò con lắc lò xo là: ${\rm{k = m}}{\omega ^2} = 0,2.15,{7^2} = 49,3{\rm{ N/m}}$

Độ lớn lực đàn hồi lúc đó là: ${F_{dh}} = k\Delta {l_{max}} = 49,3.0,04 = 3{\rm{ N}}$

Một số dao động điều hòa thường gặp 1.28

Một con lắc đơn gồm vật nhỏ treo vào sợi dây có chiều dài 2,23 m tại nơi có gia tốc trọng trường g. Đồ thị vận tốc – thời gian của vật nhỏ khi con lắc dao động như ở Hình 1.15. Xác định:

a) Gia tốc trọng trường tại nơi treo con lắc.

b) Gia tốc cực đại của vật.

c) Li độ của vật tại thời điểm t = 2,00 s.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng và đồ thị trong dao động điều hòa.

- Tần số góc : $\omega = \frac{{2\pi }}{T}$

- Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

- Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

- Li độ ${\rm{x = }} \pm \sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} $

Lời giải chi tiết:

a) Từ đồ thị, dễ thấy chu kì T = 3 s.

Gia tốc trọng trường tại nơi treo con lắc là: ${\rm{g = }}\frac{{4{\pi ^2}l}}{{{T^2}}} = \frac{{4{\pi ^2}2,23}}{{{3^2}}} = 9,78{\rm{ m/}}{{\rm{s}}^2}$

b) Tần số góc $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{3}{\rm{ rad/s}}$

Biên độ dao động của vật là: $A = \frac{{{v_{{\rm{max}}}}}}{\omega } = \frac{{4.3}}{{2\pi }} = 1,91{\rm{ cm}}$

Gia tốc cực đại của vật là: ${a_{max}} = {\omega ^2}A = {\left( {\frac{{2\pi }}{3}} \right)^2}{\rm{.1,91 = 8,38 cm/}}{{\rm{s}}^2}$

c) Tại thời điểm t = 2,00 s thì vận tốc v = -3,5 cm/s.

Li độ ${\rm{x = }} \pm \sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} {\rm{ = }} \pm \sqrt {1,{{91}^2} - {{\left( {\frac{{ - 3,5}}{{2\pi /3}}} \right)}^2}} {\rm{ = }} \pm {\rm{0,925 cm}}$

Tại t = 2 s, vật đang chuyển động nhanh dần theo chiều âm của trục tọa độ

=> Vật đi từ biên dương đến VTCB

=> x > 0

=> x = 0,925 cm

Một số dao động điều hòa thường gặp 1.29

Một đồng hồ quả lắc chạy đúng giờ nếu con lắc đơn của nó có chu kì 1,000 s, khi treo ở nơi có gia tốc trọng trường 9,800 m/s² .

a) Xác định chiều dài dây treo con lắc đơn của đồng hồ.

b) Khi được vận chuyển tới một địa phương khác, đồng hồ này chạy chậm 90,00 s mỗi ngày. Xác định gia tốc trọng trường tại nơi đó.

c) Để đồng hồ chạy đúng giờ tại địa phương mới này, người ta cần điều chỉnh lại chiều dài dây treo con lắc như thế nào?

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa.

- Chu kì dao động : $T = 2\pi \sqrt {\frac{l}{g}} $

Lời giải chi tiết:

a) Chiều dài dây treo con lắc đơn của đồng hồ là: $l = \frac{{g{T^2}}}{{4{\pi ^2}}} = \frac{{9,8.1}}{{4{\pi ^2}}} = 0,248{\rm{ m}}$

b) Ở nơi ban đầu, con lắc đồng hồ dao động 86400 T trong 86400 s.

Ở nơi mới, con lắc đồng hồ dao động 86400 T’ trong 86400 + 90 = 86490 s.

$\begin{array}{l} \Rightarrow \frac{T}{{T'}} = \frac{{86400}}{{86490}} = \frac{{960}}{{961}}\\\end{array}$

Mà $T = 2\pi \sqrt {\frac{l}{g}} ;T' = 2\pi \sqrt {\frac{l}{{g'}}} $

$\begin{array}{l} \Rightarrow \frac{{g'}}{g} = {\left( {\frac{T}{{T'}}} \right)^2}\\ \Rightarrow g' = g{\left( {\frac{T}{{T'}}} \right)^2} = 9,8.{\left( {\frac{{960}}{{961}}} \right)^2} = 9,78{\rm{ m/}}{{\rm{s}}^2}\end{array}$

c) Để T’=T=1 s

$\begin{array}{l} \Rightarrow 2\pi \sqrt {\frac{{l'}}{{g'}}} = 1\\ \Rightarrow l' = \frac{{g'}}{{4{\pi ^2}}} = \frac{{9,78}}{{4{\pi ^2}}} = 0,2477{\rm{ m}}\end{array}$

Để đồng hồ chạy đúng giờ tại địa phương mới này, người ta cần điều chỉnh lại chiều dài dây treo con lắc ngắn lại với chiều dài mới là 0,2477 m.

Một số dao động điều hòa thường gặp 1.30

Một con lắc đơn gồm sợi dây có chiều dài 1,20 m và vật có khối lượng 0,500 kg. Treo con lắc tại nơi có gia tốc trọng trường 9,81 m/s² . Kéo vật ra khỏi vị trí cân bằng sao cho sợi dây tạo với phương thẳng đứng một góc α₀ rồi thả tay cho vật dao động không vận tốc đầu. Bỏ qua mọi lực cản. Tính tốc độ của vật khi nó qua vị trí cân bằng và độ lớn lực căng của dây treo khi đó trong trường hợp:

a) α₀ = 8,00^o.

b) α₀ = 30,0^o.

Phương pháp giải:

Vận dụng kiến thức đã học về:

Con lắc đơn:

- Khi α₀ < 10^o, con lắc dao động với biên độ nhỏ, nên được coi gần đúng là dao động điều hòa.

+ Tần số góc: $\omega = \sqrt {\frac{g}{l}} $

+ Biên độ của con lắc: $A = l{\alpha _o}$

+ Tốc độ của vật khi qua VTCB: ${v_{max}} = \omega A$

- Khi góc α₀ > 10^o, chuyển động của con lắc đơn không phải dao động điều hoà.

Định luật bảo toàn cơ năng.

Trong chuyển động tròn, ${\vec F_{ht}} = \vec T + \vec P$; ${F_{ht}}{\rm{ = }}\frac{{m{v^2}}}{l}$

Lời giải chi tiết:

a) Khi α₀ = 8^o < 10^o, con lắc dao động với biên độ nhỏ, nên được coi gần đúng là dao động điều hòa với tần số góc là $\omega = \sqrt {\frac{g}{l}} = \sqrt {\frac{{9,81}}{{1,2}}} = 2,86{\rm{ rad/s}}$

Biên độ của con lắc: $A = l{\alpha _o} = 1,2.8.\frac{\pi }{{180}} = 0,168{\rm{ m}}$

Tốc độ của vật khi qua VTCB: ${v_{max}} = \omega A = 2,86.0,168 = 0,48{\rm{ m/s}}$

Ở VTCB, tổng hợp trọng lực và lực căng dây treo tác dụng lên vật đóng vai trò là lực hướng tâm:

$\begin{array}{l}T - P = {F_{ht}}{\rm{ = }}\frac{{mv_{max}^2}}{l} \Rightarrow T = P + \frac{{mv_{max}^2}}{l}\\ \Rightarrow T = 0,5.9,81 + \frac{{0,5.0,{{48}^2}}}{{1,2}}{\rm{ = 5 N}}\end{array}$

b) Khi góc α₀ = 30^o, dao động của con lắc đơn không phải dao động điều hoà. Chọn gốc thế năng hấp dẫn tại điểm O, áp dụng định luật bảo toàn cơ năng cho chuyển động của con lắc đơn ở môi trường không có lực cản.

$\begin{array}{l}{{\rm{W}}_O} = {{\rm{W}}_A} \Leftrightarrow \frac{1}{2}mv_{max}^2 = mgl\left( {1 - \cos {\alpha _0}} \right)\\ \Leftrightarrow {v_{max}} = \sqrt {2gl\left( {1 - \cos {\alpha _0}} \right)} = \sqrt {2gl\left( {1 - \cos 30} \right)} = 1,78{\rm{ m/s}}{\rm{.}}\end{array}$

Lực căng dây:

$\begin{array}{l}T = P + \frac{{mv_{max}^2}}{l}\\ \Rightarrow T = 0,5.9,81 + \frac{{0,5.1,{{78}^2}}}{{1,2}}{\rm{ = 6,23 N}}\end{array}$

Năng lượng trong dao động điều hòa 1.31

Một con lắc lò xo gồm lò xo khối lượng không đáng kể, độ cứng k, một đầu cố định và một đầu gắn với viên bi nhỏ khối lượng m. Con lắc này đang dao động điều hoà có cơ năng

A. tỉ lệ nghịch với độ cứng k của lò xo.

B. tỉ lệ với bình phương biên độ dao động.

C. tỉ lệ với bình phương chu kì dao động.

D. tỉ lệ nghịch với khối lượng m của viên bi.

Phương pháp giải:

Vận dụng kiến thức đã học về cơ năng của dao động điều hòa: ${\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2} = {\rm{const}}$

Lời giải chi tiết:

Đáp án: B. tỉ lệ với bình phương biên độ dao động.

Năng lượng trong dao động điều hòa 1.32

Phát biểu nào sau đây sai? Cơ năng của vật dao động điều hoà

A. bằng thế năng khi vật ở vị trí biên.

B. bằng động năng khi vật ở vị trí cân bằng.

C. bằng động năng khi vật ở vị trí biên.

D. bằng tổng động năng và thế năng tại mọi vị trí.

Phương pháp giải:

Vận dụng kiến thức đã học về cơ năng của dao động điều hòa: ${\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}mv_{max}^2 = const$

Lời giải chi tiết:

Cơ năng của vật dao động điều hòa: ${\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}mv_{max}^2 = const$

Đáp án: C. bằng động năng khi vật ở vị trí biên.

Năng lượng trong dao động điều hòa 1.33

Treo quả cầu vào sợi dây mảnh không co giãn để tạo thành một con lắc đơn. Trong quá trình dao động điều hoà của con lắc đơn đó, có sự biến đổi qua lại giữa

A. động năng và thế năng đàn hồi.

B. thế năng đàn hồi và thế năng hấp dẫn.

C. thế năng đàn hồi và cơ năng.

D. động năng và thế năng hấp dẫn.

Phương pháp giải:

Vận dụng kiến thức đã học về cơ năng của dao động điều hòa: ${\rm{W}} = {{\rm{W}}_{\rm{d}}} + {{\rm{W}}_t} = {\rm{const}}$

Lời giải chi tiết:

Đáp án: D. động năng và thế năng hấp dẫn.

Năng lượng trong dao động điều hòa 1.34

Một vật nhỏ khối lượng 0,10 kg dao động điều hoà theo phương trình x = 8,0cos10,0t (x tính bằng cm; t tính bằng s). Động năng cực đại của vật là

A. 32 mJ.

B. 16 mJ.

C. 64 mJ.

D. 28 mJ.

Phương pháp giải:

Vận dụng kiến thức đã học về động năng cực đại của dao động điều hòa: ${{\rm{W}}_{dmax}} = \frac{1}{2}mv_{max}^2$

Lời giải chi tiết:

Động năng cực đại của vật là ${{\rm{W}}_{dmax}} = \frac{1}{2}mv_{max}^2 = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}0,{1.10^2}.0,{08^2} = 32{\rm{ mJ}}$

Đáp án: A. 32 mJ.

Năng lượng trong dao động điều hòa 1.35

Một con lắc lò xo gồm vật có khối lượng 0,20 kg gắn vào lò xo nhẹ có độ cứng 50,0 N/m. Tính cơ năng của con lắc khi nó dao động điều hoà với biên độ 4,0 cm.

Phương pháp giải:

Vận dụng kiến thức đã học về đại lượng cơ năng trong dao động điều hòa: ${\rm{W}} = \frac{1}{2}k{A^2}$

Lời giải chi tiết:

Cơ năng của vật là : ${\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}50.0,{04^2} = 0,04{\rm{ J}}$

Năng lượng trong dao động điều hòa 1.36

Đồ thị Hình 1.16 biểu diễn sự thay đổi động năng theo li độ của một vật dao động điều hoà có chu kì 0,12 s. Xác định:

a) Khối lượng của vật.

b) Thế năng khi vật ở vị trí có li độ 1,0 cm.

c) Vị trí tại đó vật có động năng bằng thế năng.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng và đồ thị của dao động điều hòa:

- Cơ năng: ${\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \frac{1}{2}k{A^2} = \frac{1}{2}mv_{max}^2 = const$

- Tần số góc : $\omega = \frac{{2\pi }}{T}$

- Tốc độ cực đại của vật: ${v_{max}} = \omega A$

- Khi W_d = nW_t thì ${{\rm{W}}_t}{\rm{ = }} \pm \frac{{\rm{W}}}{{\sqrt {n + 1} }}$

Lời giải chi tiết:

Tần số góc của vật là : $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,12}} = 52,36{\rm{ rad/s}}$

Từ đồ thị, dễ thấy A = 2 cm; W_dmax = 0,08 J.

a) Tốc độ cực đại của vật: ${v_{max}} = \omega A = 52,36.0,02 = 1,047{\rm{ m/s}}$

Khối lượng của vật là : $m = \frac{{2{W_{dmax}}}}{{v_{max}^2}} = \frac{{2.0,08}}{{1,{{047}^2}}} = 0,15{\rm{ kg}}$

b) Tại x = 1 cm, W_d = 0,06 J

Thế năng của vật là: W_t = W – W_d = W_dmax – W_d = 0,08 – 0,06 J

c) Khi vật có W_d = nW_t thì ${{\rm{W}}_t}{\rm{ = }} \pm \frac{{\rm{W}}}{{\sqrt {n + 1} }}$

$\frac{1}{2}m{\omega ^2}{x^2} = \frac{1}{{n + 1}}.\frac{1}{2}m{\omega ^2}{A^2} \Leftrightarrow x = \pm \frac{A}{{\sqrt {n + 1} }}$

Với n = 1 thì $x = \pm \frac{A}{{\sqrt 2 }} = \pm \frac{2}{{\sqrt 2 }} = \pm 1,4{\rm{ cm}}$

Năng lượng trong dao động điều hòa 1.37

Một con lắc lò xo dao động điều hoà với cơ năng 1,0 J. Biết rằng biên độ của vật dao động là 10,0 cm và tốc độ cực đại của vật là 1,2 m/s. Hãy xác định:

a) Khối lượng của vật gắn với lò xo.

b) Độ cứng của lò xo.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng của dao động điều hòa:

- Cơ năng: ${\rm{W}} = {{\rm{W}}_{tmax}}{\rm{ = }}{{\rm{W}}_{dmax}} = \frac{1}{2}k{A^2} = \frac{1}{2}mv_{max}^2 = const$

Lời giải chi tiết:

a) Ta có ${\rm{W}} = {{\rm{W}}_{dmax}} = \frac{1}{2}mv_{max}^2 \Rightarrow m = \frac{{2{\rm{W}}}}{{v_{max}^2}} = \frac{{2.1}}{{1,{2^2}}} = 1,4{\rm{ kg}}$

b) Ta có ${\rm{W}} = {{\rm{W}}_{tmax}} = \frac{1}{2}k{A^2} \Rightarrow k = \frac{{2{\rm{W}}}}{{{A^2}}} = \frac{{2.1}}{{0,{1^2}}} = 200{\rm{ N/m}}$

Năng lượng trong dao động điều hòa 1.38

Đồ thị Hình 1.17 mô tả sự thay đổi động năng của một vật dao động điều hoà có khối lượng 0,40 kg theo thời gian. Xác định:

a) Chu kì của dao động.

b) Tốc độ cực đại của vật.

c) Biên độ của dao động.

d) Gia tốc cực đại của vật dao động.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng và đồ thị của dao động điều hòa:

- Cơ năng: ${\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \frac{1}{2}k{A^2} = \frac{1}{2}mv_{max}^2 = const$

- Động năng và thế năng đều biến thiên tuần hoàn với chu kì bằng ½ chu kì dao động của vật.

- Tần số góc : $\omega = \frac{{2\pi }}{T}$

- Khi vật ở vị trí biên $(x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A$

- Khi vật ở vị trí cân bằng $(x = 0);v = {v_{max}} = \pm \omega A;a = 0$

Lời giải chi tiết:

a) Chu kì của năng lượng là T_w = 0,4 s

=> Chu kì của dao động là T = 2T_w = 2.4 = 0,8 s.

b) Ta có ${\rm{W}} = {{\rm{W}}_{dmax}} = \frac{1}{2}mv_{max}^2 \Rightarrow {v_{max}} = \sqrt {\frac{{2{\rm{W}}}}{m}} = \sqrt {\frac{{2,0.16}}{{0,4}}} = 0,28{\rm{ m/s}}$

c) Tần số góc dao động: $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,8}} = 7,9{\rm{ rad/s}}$

Ta có ${v_{max}} = \omega A{\rm{ }} \Rightarrow A = \frac{{{v_{max}}}}{\omega } = \frac{{0,28}}{{7,9}} = 0,036{\rm{ m}}$

d) Gia tốc cực đại của vật: ${a_{max}} = {\omega ^2}A{\rm{ = 7,}}{{\rm{9}}^2}.0,036 = 2,25{\rm{ m/}}{{\rm{s}}^2}$

Năng lượng trong dao động điều hòa 1.39

Một con lắc lò xo dao động điều hoà trên mặt bàn nằm ngang không ma sát với tần số 2,0 Hz. Khối lượng của vật gắn với lò xo là 0,20 kg. Tại thời điểm ban đầu, vật ở vị trí có li độ 5,0 cm và vận tốc – 0,30 m/s.

a) Viết phương trình li độ của vật.

b) Xác định tốc độ cực đại và gia tốc cực đại của vật.

c) Tìm vị trí của vật tại thời điểm 0,40 s.

d) Tìm cơ năng dao động của con lắc.

e) Tìm các vị trí mà tại đó con lắc có động năng gấp 3 lần thế năng.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà: $x = A\cos \left( {\omega t + \varphi } \right)$

- Tần số góc $\omega = 2\pi f$

- Hệ thức vuông pha trong dao động điều hòa: $\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1$

- Tốc độ cực đại của vật:${v_{max}} = \omega A$

- Gia tốc cực đại của vật: ${a_{max}} = \omega {A^2}$

- Cơ năng của vật: $W = \frac{1}{2}mv_{\max }^2 = \frac{1}{2}k{A^2}$

- Khi ${W_d} = n{W_t}$ thì $x = \pm \frac{A}{{\sqrt {n + 1} }}$

Lời giải chi tiết:

a) Tần số góc: $\omega = 2\pi f = 2\pi .2 = 4\pi {\rm{ rad/s}}$

Ta có hệ thức vuông pha giữa li độ và vận tốc:

$\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1$

$ \Rightarrow A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{5^2} + \frac{{{{\left( { - 30} \right)}^2}}}{{{{\left( {4\pi } \right)}^2}}}} = 5,54{\rm{ cm}}$

Phương trình li độ của vật có dạng: $x = A\cos \left( {\omega t + \varphi } \right) \Leftrightarrow x = 5,54\cos \left( {4\pi t + \varphi } \right)$

Tại t = 0, vật có vận tốc v < 0 => vật đang chuyển động ngược chiều dương

=> $0 < \varphi < \pi {\rm{ rad}}$

Tại t = 0, vật có li độ x = 5 cm, thay vào phương trình li độ, ta được:

$5 = 5,54\cos \varphi \Rightarrow \cos \varphi = \frac{5}{{5,54}} \Rightarrow \varphi = 0,45$

Vậy phương trình li độ của vật là: $x = 5,54\cos \left( {4\pi t + 0,45} \right){\rm{ }}\left( {{\rm{cm}}} \right)$

b) Tốc độ cực đại của vật là: ${v_{max}} = \omega A = 4\pi .5,54 = 69,62{\rm{ cm/s}}$

Gia tốc cực đại của vật là: ${a_{max}} = \omega {A^2} = 4\pi .5,{54^2} = 385,68{\rm{ cm/}}{{\rm{s}}^2}$

c) Thay t = 0,4 vào phương trình li độ:

$x = 5,54\cos \left( {4\pi .0,4 + 0,45} \right) = 3,83{\rm{ cm}}$

Vậy tại thời điểm t = 0,4 s, vật ở vị trí li độ x = 3,83 cm.

d) Cơ năng dao động của con lắc là: $W = \frac{1}{2}mv_{max}^2 = \frac{1}{2}.0,2.0,{696^2} = 0,048{\rm{ J}}$

e) Từ đề bài, ta có:

$\begin{array}{l}{W_d} = 3{W_t}\\ \Rightarrow x = \pm \frac{A}{{\sqrt {n + 1} }} = \pm \frac{{5,54}}{{\sqrt {3 + 1} }}\\ \Rightarrow x = \pm 2,77{\rm{ cm}}\end{array}$

Tại 4 vị trí tương ứng với li độ $x = \pm 2,77{\rm{ cm}}$, con lắc có động năng gấp 3 lần thế năng.

Năng lượng trong dao động điều hòa 1.40

Trong phân tử hydrochloric acid (HCl), nguyên tử clorine (Cl) và nguyên tử hydrogen (H) có thể được coi là kết nối với nhau giống như có một lò xo nối giữa chúng. Vì khối lượng của nguyên tử clorine lớn hơn nhiều so với khối lượng của nguyên tử hydrogen nên có thể coi gần đúng là nguyên tử clorine đứng yên còn nguyên tử hydrogen dao động điều hòa quanh một vị trí cân bằng.

Hình 1.18 biểu diễn thế năng tương tác giữa hai nguyên tử trong phân tử HCl. Dựa vào đồ thị hãy xác định tần số dao động của nguyên tử hydrogen. Biết rằng khối lượng của nguyên tử hydrogen là 1,67.10^–27 kg.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa.

- Biên độ dao động $A = \frac{S}{2}$với S là quỹ đạo chuyển động của vật.

- Cơ năng dao động: ${\rm{W = }}{{\rm{W}}_{t\max }}{\rm{ = }}\frac{1}{2}k{A^2}$

- Tần số dao động: $f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} $

Lời giải chi tiết:

Biên độ dao động của nguyên tử H là: $A = \frac{{0,17 - 0,09}}{2} = 0,04{\rm{ nm}}$

Cơ năng của nguyên tử H là: ${\rm{W = }}{{\rm{W}}_{t\max }}{\rm{ = }}\frac{1}{2}k{A^2} = {4.10^{ - 19}}{\rm{ J}}$

$ \Rightarrow k = \frac{{2{W_{t\max }}}}{{{A^2}}} = \frac{{{{2.4.10}^{ - 19}}}}{{{{\left( {0,{{04.10}^{ - 9}}} \right)}^2}}} = 500{\rm{ N/m}}$

=> Tần số f của nguyên tử H là: $f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} = \frac{1}{{2\pi }}\sqrt {\frac{{500}}{{1,{{67.10}^{--27}}}}} = 8,{7.10^{13}}{\rm{ Hz }}$

Năng lượng trong dao động điều hòa 1.41

Một con lắc lò xo gồm vật có khối lượng 0,500 kg gắn vào đầu tự do của một lò xo nhẹ có độ cứng 20,0 N/m. Con lắc dao động theo phương nằm ngang với biên độ 4,00 cm.

a) Tính tốc độ cực đại của vật dao động.

b) Tính cơ năng dao động của con lắc.

c) Tính động năng và tốc độ của vật khi nó ở vị trí có li độ 2,00 cm.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng trong dao động điều hòa.

- Tốc độ cực đại của vật: ${v_{\max }} = \omega A$

- Cơ năng dao động: $W = {W_{t\max }}$

- Tốc độ của vật: $\left| v \right| = \omega \sqrt {{A^2} - {x^2}} $

- Động năng của vật: ${W_d} = \frac{1}{2}m{v^2}$

Lời giải chi tiết:

Tần số góc $\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{20}}{{0,5}}} = 6,32{\rm{ rad/s}}$

a) Tốc độ cực đại của vật dao động là: ${v_{\max }} = \omega A = 6,32.4 = 25,3{\rm{ cm/s}}$

b) Cơ năng dao động của con lắc là: $W = {W_{t\max }} = \frac{1}{2}k{A^2} = \frac{1}{2}.20.0,{04^2} = 0,016{\rm{ J}}$

c) Khi vật ở vị trí li độ 2,00 cm:

Tốc độ của vật là: $\left| v \right| = \omega \sqrt {{A^2} - {x^2}} = 6,32\sqrt {{4^2} - {2^2}} = 21,9{\rm{ cm/s}}$

Động năng của vật là: ${W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.0,5.0,{219^2} = 0,012{\rm{ J}}$

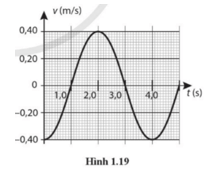
Năng lượng trong dao động điều hòa 1.42

Hình 1.19 là đồ thị vận tốc – thời gian của một con lắc đơn dao động điều hoà với cơ năng 9,6 mJ. Hãy xác định:

a) Khối lượng của vật nhỏ.

b) Biên độ của dao động.

c) Li độ của con lắc tại thời điểm 1,5 s.

Hình 1.19 là đồ thị vận tốc – thời gian của một con lắc đơn dao động điều hoà

Phương pháp giải:

Vận dụng kiến thức đã học về đồ thị và các đại lượng trong dao động điều hòa.

- Tốc độ cực đại của vật: ${v_{\max }} = \omega A$

- Cơ năng dao động: $W = {W_{t\max }} = {W_{d\max }} = \frac{1}{2}k{A^2} = \frac{1}{2}mv_{\max }^2$

- Li độ của vật: $x = \pm \sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} $

- Vận tốc góc: $\omega = \frac{{2\pi }}{T}$

Lời giải chi tiết:

a) Khối lượng của vật là: $m = \frac{{2{W_{d\max }}}}{{v_{\max }^2}} = \frac{{2.9,{{6.10}^{ - 3}}}}{{0,{4^2}}} = 0,12{\rm{ kg}}$

b) Từ đồ thị, chu kì của vật là T = 4 s.

Tần số góc của vật là: $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{4} = \frac{\pi }{2}{\rm{ rad/s}}$

Độ cứng k của vật là: $k = m{\omega ^2} = 0,12.{\left( {\frac{\pi }{2}} \right)^2} = 0,3{\rm{ N/m}}$

Biên độ của dao động là: $A = \sqrt {\frac{{2{W_{t\max }}}}{k}} = \sqrt {\frac{{2.9,{{6.10}^{ - 3}}}}{{0,3}}} = 0,25{\rm{ m}}$

c) Từ đồ thị, dễ thấy tại t = 1,5 s, vật có vận tốc v = 0,28 m/s và tăng dần lên v_max.

=> Vật đang chuyển động theo chiều dương và x < 0.

Li độ của con lắc tại thời điểm 1,5 s: \(x = - \sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} = - \sqrt {0,{{25}^2} - \frac{{0,{{28}^2}}}{{{{\left( {{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/

{\vphantom {\pi 2}}\right.\kern-\nulldelimiterspace}

\!\lower0.7ex\hbox{$2$}}} \right)}^2}}}} = - 0,18{\rm{ m}}\)

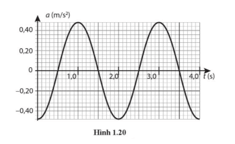
Năng lượng trong dao động điều hòa 1.43

Hình 1.20 là đồ thị gia tốc – thời gian của một vật có khối lượng 0,15 kg đang dao động điều hoà. Hãy xác định:

a) Biên độ của dao động.

b) Vận tốc của vật tại thời điểm t = 1,0 s.

c) Động năng cực đại của vật.

d) Thế năng và vị trí của vật tại thời điểm t = 2,0 s.

Hình 1.20 là đồ thị gia tốc – thời gian của một vật có khối lượng 0,15 kg

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

a) Từ đồ thị, ta thấy gia tốc cực đại a_max = 0,48 m/s² và chu kì T = 2 s.

Tần số góc của vật: $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{2} = \pi {\rm{ rad/s}}$

Mà ${a_{\max }} = {\omega ^2}A$

Biên độ dao động của vật là: $A = \frac{{{a_{\max }}}}{{{\omega ^2}}} = \frac{{0,48}}{{{\pi ^2}}} = 0,049{\rm{ m}}$

b) Vận tốc của vật tại thời điểm t = 1,0 s.

Khi t = 1 s, $a = {a_{\max }} = {\omega ^2}A$

=> Li độ x = -A, vật chuẩn bị chuyển động theo chiều dương.

=> Vận tốc v = 0, vận tốc chuẩn bị dương.

c) Tốc độ cực đại của vật là: ${v_{\max }} = \omega A = \frac{{{a_{\max }}}}{\omega } = \frac{{0,48}}{\pi } = 0,153{\rm{ m/s}}$

Động năng cực đại của vật là: ${W_{d\max }} = \frac{1}{2}mv_{_{\max }}^2 = \frac{1}{2}0,15.0,{153^2}{\rm{ = 1,8}}{\rm{.1}}{{\rm{0}}^{ - 3}}{\rm{ J}}$

d) Thế năng và vị trí của vật tại thời điểm t = 2,0 s.

Tại t = 2 s, a = - a_max => x = A = 0,049 m.

Thế năng của vật lúc này là: ${W_t} = {W_{t\max }} = {W_{d\max }}{\rm{ = 1,8}}{\rm{.1}}{{\rm{0}}^{ - 3}}{\rm{ J}}$

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.44

Khi nói về dao động tắt dần, phát biểu nào dưới đây là không đúng?

A. Biên độ giảm dần theo thời gian.

B. Cơ năng dao động không thay đổi.

C. Tác dụng của lực cản môi trường là nguyên nhân chính làm cho dao động tắt dần.

D. Sự tắt dần của dao động diễn ra nhanh hay chậm phụ thuộc vào cơ năng ban đầu của dao động và lực cản của môi trường.

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

Đáp án: B. Cơ năng dao động không thay đổi.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.45

Dao động của quả lắc đồng hồ không tắt dần là vì

A. lực cản tác dụng lên quả lắc không đáng kể.

B. quả lắc có khối lượng lớn nên cơ năng dao động lớn, vì vậy sự tắt dần xảy ra rất chậm nên không phát hiện ra dao động của nó tắt dần.

C. trong đồng hồ có một nguồn năng lượng dự trữ, năng lượng mất đi sau mỗi chu kì dao động được bù lại từ nguồn năng lượng dự trữ này.

D. trọng lực luôn thực hiện công lên quả lắc trong suốt quá trình nó dao động.

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

Đáp án: C. trong đồng hồ có một nguồn năng lượng dự trữ, năng lượng mất đi sau mỗi chu kì dao động được bù lại từ nguồn năng lượng dự trữ này.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.46

Phát biểu nào sau đây là không đúng khi nói về dao động cưỡng bức?

A. Biên độ của dao động cưỡng bức không đổi.

B. Tần số của dao động bằng tần số của ngoại lực cưỡng bức.

C. Tần số ngoại lực càng lớn thì biên độ của dao động càng lớn.

D. Với một tần số ngoại lực xác định, biên độ ngoại lực càng lớn thì biên độ của dao động càng lớn.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Đáp án: C. Tần số ngoại lực càng lớn thì biên độ của dao động càng lớn.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.47

Phát biểu nào sau đây đúng?

A. Dao động của quả lắc đồng hồ là dao động cưỡng bức.

B. Dao động cưỡng bức đang xảy ra cộng hưởng, nếu lực cản của môi trường tác dụng lên vật dao động giảm thì biên độ dao động cũng giảm.

C. Hiện tượng cộng hưởng trong dao động cưỡng bức luôn có hại.

D. Dao động cưỡng bức lúc ổn định, tốc độ cung cấp năng lượng của ngoại lực bằng tốc độ mất năng lượng của dao động.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Đáp án: D. Dao động cưỡng bức lúc ổn định, tốc độ cung cấp năng lượng của ngoại lực bằng tốc độ mất năng lượng của dao động.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.48

Một con lắc lò xo có chu kì dao động riêng T₀ = 1 s. Tác dụng các lực cưỡng bức biến đổi tuần hoàn theo phương trùng với trục của lò xo. Lực cưỡng bức nào dưới đây làm cho con lắc dao động mạnh nhất?

A. F = 3F₀cosπt.

B. F = F₀cos2πt.

C. F = 3F₀cos2πt.

D. F = 2F₀cosπt.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Đáp án: C. F = 3F₀cos2πt.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.49

Một con lắc lò xo nằm ngang, lò xo có khối lượng không đáng kể và có độ cứng k = 100,0 N/m. Vật nhỏ m có khối lượng 0,20 kg. Tác dụng vào vật m một ngoại lực F = F₀cos(2πft) với F₀ không đổi còn f thay đổi được và có phương trùng với trục của lò xo. Tìm f để biên độ dao động của vật m lớn nhất. Bỏ qua sức cản tác dụng lên vật.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Biên độ dao động của vật m lớn nhất khi xảy ra cộng hưởng:

$f = {f_0}{\rm{ = }}\frac{1}{{2\pi }}\sqrt {\frac{k}{m}} {\rm{ = }}\frac{1}{{2\pi }}\sqrt {\frac{{100}}{{0,2}}} {\rm{ = 3,6 Hz}}$

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.50

Một con lắc lò xo treo trên trần của toa tàu ngay vị trí phía trên trục bánh xe. Biết chiều dài mỗi thanh ray là L = 12 m và khi tàu chạy thẳng đều với tốc độ v = 20,0 m/s thì vật m gắn ở đầu dưới của lò xo dao động với biên độ lớn nhất. Tìm chu kì dao động riêng T₀ của con lắc.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức và thanh ray đường sắt.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

- Thanh ray: Tuyến đường ray có từ 2 đường ray trở lên, giúp định hướng và chuyển hướng bánh xe của tàu. Mỗi đường ray tách làm nhiều thanh ray để khi tàu ma sát với đường ray, sự giãn nở vì nhiệt của thanh ray không làm biến dạng tuyến đường ray.

Lời giải chi tiết:

Mỗi lần đi hết một thanh ray và chuyển sang thanh ray khác, toa tàu hạ xuống và nâng lên dưới tác dụng của trọng lực, từ đó tạo thành ngoại lực tác dụng vào vật m.

=> Thời gian đi hết một thanh ray là chu kì của ngoại lực tác dụng lên vật m.

Vật m dao động với biên độ lớn nhất.

=> Đang xảy ra hiện tượng cộng hưởng.

=> Chu kì dao động riêng của con lắc là: $T = {T_0}{\rm{ = }}\frac{L}{v}{\rm{ = }}\frac{{12}}{{20}}{\rm{ = 0,6 s}}$

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.51

Nêu một số ví dụ thực tế về dao động tắt dần. Trong ví dụ đã nêu, dao động tắt dần là có lợi hay có hại?

Phương pháp giải:

Vận dụng kiến thức đã học về dao động tắt dần.

- Dao động tắt dần có biên độ giảm dần theo thời gian.

Lời giải chi tiết:

Một số gợi ý:
– Xe chạy trên cầu, đã tác động làm cầu dao động. Khi xe vượt qua cầu, dao động của cầu sẽ tắt dần. Sự tắt dần dao động của cầu trong trường hợp này là có lợi.
– Khi em bé chơi xích đu, nếu không có lực đẩy liên tục, xích đu sẽ dao động tắt dần. Sự tắt dần dao động của xích đu trong trường hợp này là có hại.

– Do tác dụng của bộ phận giảm xóc, dao động của xe máy và người ngồi trên xe sau khi xe đi qua chỗ xóc bị tắt dần. Dao động tắt dần này là có lợi, giúp giảm sự khó chịu cho người ngồi trên xe.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.52

Nêu một số ví dụ về dao động cưỡng bức xảy ra cộng hưởng trong một thiết bị khi đang vận hành tại gia đình.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Khi máy giặt làm việc ở chế độ vắt, lồng giặt quay rất nhanh đã tác dụng một lực tuần hoàn lên vỏ máy. Nếu tần số quay của lồng giặt bằng tần số dao động riêng của vỏ máy thì máy giặt sẽ rung lắc rất mạnh.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.53

Một chiếc thuyền đang dao động bởi những con sóng xô mạn thuyền. Dao động của thuyền có phải là dao động cưỡng bức không?

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Dao động của thuyền là một dao động cưỡng bức.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.54

Hãy tìm hiểu về cấu tạo của giảm xóc xe máy và cho biết vì sao khi xe máy đi qua chỗ xóc thì dao động của hệ người đi và xe tắt rất nhanh (cỡ không quá nửa chu kì).

Phương pháp giải:

Vận dụng kiến thức đã học về dao động tắt dần và bộ phận giảm xóc xe máy.

- Dao động tắt dần có biên độ giảm dần theo thời gian.

Lời giải chi tiết:

Cấu tạo chính của bộ phận giảm xóc xe máy gồm hai phần:

– Lò xo gắn giữa khung xe và trục bánh xe.

– Pít-tông chuyển động trong xi lanh dầu.

Khi xe qua chỗ xóc, lò xo nén, dãn đàn hồi làm cho khung xe dao động lên xuống. Khi đó, pít-tông dao động trong xi lanh dầu. Lực ma sát lớn trong dầu làm cho dao động của pít-tông tắt dần rất nhanh nên dao động của khung xe cũng tắt dần theo.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.55

Trong lịch sử có những trận động đất đã phá hủy các nhịp cầu của đường cao tốc trên cao. Thực tế đã xảy ra là nhịp cầu ngang qua những nơi quan trọng được gia cố cẩn thận hơn thì bị sập; những nhịp cầu khác lại đứng vững. Bằng hiểu biết của mình, em hãy dự đoán những nguyên nhân nào dẫn đến hiện tượng trên và bài học rút ra khi xây dựng cầu.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Nếu tần số rung lắc của mặt đất khi xảy ra động đất bằng với tần số dao động riêng của nhịp cầu thì xảy ra hiện tượng cộng hưởng làm cho nhịp cầu rung lắc rất mạnh. Khi xây dựng các công trình như cầu, toà nhà cao tầng tại một vị trí, cần nghiên cứu điều kiện địa chất nơi đó (lịch sử từng xảy ra động đất, khoảng tần số rung chấn…) để thiết kế các công trình có tần số riêng khác xa với khoảng tần số rung chấn.

Một giải pháp khác là khi xây dựng các công trình ở các khu vực thường xuyên xảy ra động đất, cần có hệ thống hấp thụ năng lượng dao động khi các công trình rung lắc do địa chấn. Khi đó, các dao động sau địa chấn sẽ tắt nhanh và giảm nguy cơ sập đổ.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.56

Tháng 4 năm 1983, một lữ đoàn lính diễu hành bước đều qua cầu treo Broughton của Anh. Theo các ghi chép vào thời điểm đó, cây cầu đã bị phá hủy làm nhiều người rơi xuống nước. Hãy cho biết lí do gây ra tai nạn trên và cách phòng tránh sự cố tái diễn.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Tần số nhịp bước chân của đoàn quân trùng với tần số dao động riêng của cầu làm xảy ra hiện tượng cộng hưởng.

Cách phòng tránh: Không hành quân bước đều khi đi qua cầu.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.57

Vào năm 2007, một hiện tượng gây hoảng loạn cho người dân ở một toà nhà 14 tầng tại Hà Nội. Sàn của các phòng rung chuyển làm đĩa, cốc trên bàn dịch chuyển rơi vỡ ở một số căn nhà. Nguyên nhân sau đó được tìm ra là ở gần đó có một máy đầm đất đang thi công (Hình 1.21). Hãy giải thích tại sao một máy đầm đất nhỏ mà có thể làm rung chuyển các sàn nhà của một toà chung cư hàng ngàn tấn.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Tần số của máy đầm đất bằng tần số riêng của toà nhà làm xảy ra cộng hưởng.

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.58

Một người đi bộ mỗi bước dài ΔS = 0,4 m. Người này xách một xô nước rồi bước đi đều. Biết chu kì dao động riêng của nước trong xô là 0,5 s. Người này đi với tốc độ bằng bao nhiêu thì nước trong xô sóng sánh mạnh nhất?

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

Nước trong xô sóng sánh mạnh nhất khi xảy ra cộng hưởng, chu kì dao động riêng của nước bằng chu kì nhịp bước chân của người.

$T = \frac{{\Delta S}}{v}{\rm{ = }}{{\rm{T}}_o} \Rightarrow v = \frac{{0,4}}{{0,5}}{\rm{ = 0,8 m/s}}$

Dao động tắt dần. Dao động cưỡng bức và hiện tượng cộng hưởng 1.59

Quả lắc của đồng hồ cổ treo tường có tác dụng vận hành cho đồng hồ chạy đúng giờ (Hình 1.22). Cứ sau mỗi chu kì dao động của quả lắc, do sức cản và việc vận hành hệ thống bánh răng để các kim đồng hồ chạy nên nó tiêu hao một năng lượng là ∆E = 0,100 mJ. Năng lượng này được lấy từ một quả tạ có trọng lượng P = 50,0 N treo trong hoặc ngoài đồng hồ.

a) Vì sao sau một thời gian dài đồng hồ chạy thì quả tạ bị hạ thấp xuống và ta lại phải đưa nó lên cao.

b) Nếu chạy trong thời gian t = 10,0 ngày thì quả tạ sẽ giảm độ cao bao nhiêu mét? Biết trong N = 30,0 chu kì dao động của quả lắc thì kim giây chuyển động được một vòng.

Phương pháp giải:

Vận dụng kiến thức đã học về dao động cưỡng bức.

- Dao động gây ra bởi một ngoại lực cưỡng bức biến thiên tuần hoàn được gọi là dao động cưỡng bức. Dao động cưỡng bức có tần số bằng tần số của ngoại lực cưỡng bức.

- Hiện tượng biên độ dao động cưỡng bức tăng đến giá trị cực đại khi tần số f của lực cưỡng bức bằng tần số riêng f₀ của hệ dao động được gọi là hiện tượng cộng hưởng.

Lời giải chi tiết:

a) Quả tạ dự trữ năng lượng dưới dạng thế năng trọng trường. Mỗi chu kì dao động, thế năng này giảm dần để bù cho phần năng lượng tiêu hao của quả lắc và hệ thống bánh răng. Do đó, độ cao quả tạ giảm dần.
b) Mỗi phút, kim dây chuyển động 1 vòng và con lắc đồng hồ thực hiện N = 30 chu kì.
⇒ Số chu kì con lắc thực hiện trong 10 ngày là: $10.24.60.30 = 432000{\rm{ }}T$

⇒ Tổng năng lượng tiêu hao trong 10 ngày là: $E = 432000.0,{1.10^{ - 3}} = 43,2{\rm{ J}}$
Năng lượng này bằng độ giảm thế năng trọng trường của quả tạ, do đó, độ cao quả tạ bị giảm một đoạn: $\Delta h = \frac{E}{P} = \frac{{43,2}}{{50}}{\rm{ = 0,864 m}}$