Bài 2. Mô tả dao động điều hòa trang 6, 7 SBT Vật lí 11 Kết nối tri thức với cuộc sống
Một chất điểm dao động điều hoà có chu kì T = 1 s. Tần số góc (omega ) của dao động là
2.1
Một chất điểm dao động điều hoà có chu kì T = 1 s. Tần số góc \(\omega \) của dao động là
A. \(\pi \) (rad/s) B. 2\(\pi \) (rad/s) C. 1 (rad/s) D. 2 (rad/s).
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà.
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
Lời giải chi tiết:
Ta có tần số góc \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{1} = 2\pi (rad/s)\)
Đáp án: B
2.2
Một chất điểm dao động điều hoà có tần số góc \(\omega = 10\pi \)(rad/s). Tần số của dao động là
A. 5 Hz B. 10 Hz C. 20 Hz D. 5\(\pi \) Hz.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà.
Tần số: f là số dao động mà vật thực hiện được trong một giây
Đơn vị của tần số là Héc (Kí hiệu Hz)
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
Lời giải chi tiết:
Ta có tần số góc \(\omega = 2\pi f = 10\pi = > f = \frac{\omega }{{2\pi }} = \frac{{10\pi }}{{2\pi }} = 5(Hz)\)
Đáp án :A
2.3
Một chất điểm dao động điều hoà trong thời gian 1 phút vật thực hiện được 30 dao động. Chu kì dao động của vật là
A. 2 s B. 30 s C. 0,5 s D. 1 s
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà.
Chu kì: T là khoảng thời gian để vật thực hiện được một dao động.
Tần số: f là số dao động mà vật thực hiện được trong một giây \(f = \frac{1}{T}\)
Đơn vị của tần số là Héc (Kí hiệu Hz)
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
Lời giải chi tiết:
1s vật thực hiện được số dao động là : \(30:60 = 0,5\)(dao động )
\( = > f = 0,5(Hz) = > T = \frac{1}{f} = \frac{1}{{0,5}} = 2\left( s \right)\)
Đáp án :A
2.4
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là:
\(x = 5\sqrt 3 \cos \left( {10\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\). Tần số của dao động là:
A. 10 Hz B. 20 Hz C. 10 Hz D . 5 Hz.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\).
Tần số: f là số dao động mà vật thực hiện được trong một giây \(f = \frac{1}{T}\)
Đơn vị của tần số là Héc (Kí hiệu Hz)
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
Lời giải chi tiết:
Từ phương trình ta có : \(\omega = 10\pi = > f = \frac{\omega }{{2\pi }} = \frac{{10\pi }}{{2\pi }} = 5(Hz)\)
Đáp án :D
2.5
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là:
\(x = 6\cos \left( {4\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\). Chu kì của dao động bằng:
A. 4 s B. 2 s C.0,25 s D. 0,5 s.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Chu kì: T là khoảng thời gian để vật thực hiện được một dao động.
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
Lời giải chi tiết:
Từ phương trình ta có : \(\omega = 4\pi = > T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,5(s)\)
Đáp án :D
2.6
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian
\(x = 10\cos \left( {\frac{\pi }{3}t + \frac{\pi }{2}} \right)\left( {cm} \right)\). Tại thời điểm t vật có li độ 6 cm và đang hướng về vị trí cân bằng. Sau 9 s kể từ thời điểm t thì vật đi qua li độ:
A. 3 cm đang hướng về vị trí cân bằng.
B.\( - 3\) cm đang hướng về vị trí biên.
C. 6 cm đang hướng về vị trí biên.
D. \( - 6\) cm đang hướng về vị trí cân bằng.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:
+ \(x\) là li độ dao động.
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+\(\varphi \) là pha ban đầu.
Chu kì: T là khoảng thời gian để vật thực hiện được một dao động.
Tần số: f là số dao động mà vật thực hiện được trong một giây \(f = \frac{1}{T}\)
Đơn vị của tần số là Héc (Kí hiệu Hz)
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
Lời giải chi tiết:
Từ phương trình ta có :\(\omega = \frac{\pi }{3} = > T = \frac{{2\pi }}{\omega } = \frac{{2\pi .3}}{\pi } = 6(s)\)
Tại thời điểm t vật có li độ 6 cm và đang hướng về vị trí cân bằng
=> sau \(t = 9(s) = \frac{9}{6}T = 1,5T\) \( = T + \frac{T}{2}\) thì vật ở có li độ bằng -6 cm và đang hướng về VTCB
Đáp án :D
2.7
Phương trình dao động điều hoà là \(x = 5\cos \left( {10\pi t - \frac{\pi }{2}} \right)\left( {cm} \right)\).Tính thời gian để vật đi được quãng đường 2,5 cm kẻ từ thời điểm t = 0.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Chu kì: T là khoảng thời gian để vật thực hiện được một dao động.
Quãng đường trong một dao động \(S = 4A\)
Lời giải chi tiết:
Từ phương trình ta có : \(\omega = 10\pi = > T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{10\pi }} = 0,2(s)\)
Và biên độ dao động A= 5 (cm)
Ta có \(S = 2,5 = \frac{A}{2}\)
Tại thời điểm t=0 vật ở VTCB đi ra biên dương . Để đi hết quãng đường \(S = \frac{A}{2}\)thì nó đi từ VTCB \(x = \frac{A}{2}\) => \(t = \frac{T}{{12}}\)\( = \frac{{0,2}}{{12}} = \frac{1}{{60}}(s)\)
2.8
Đồ thị li độ theo thời gian của một chất điềm dao động điều hoà được mô tả như Hình 2.1
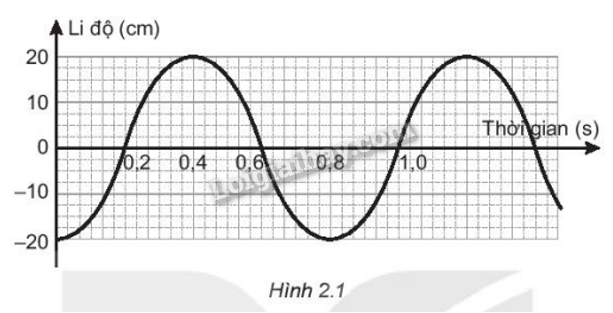
a) Xác định biên độ, chu kì và pha ban đầu của dao động.
b) Viết phương trình dao động.
c) Xác định li độ của vật ở các thời điểm 0,4 s ; 0,6 s và 0,8 s.
Phương pháp giải:
1. Vận dụng kiến thức đã học trong phần 1. Đồ thị dao động điều hoà.
2. Để tìm li độ tại thời điểm t ta thay t vào phương trình dao động hoặc quan sát đồ thị.
Lời giải chi tiết:
a) Từ đồ thị ta có
Biên độ dao động của vật : \(A = x\max = 20(cm)\)
Từ vị trí thấp nhất đến vị trí cao nhất là \(\frac{T}{2} = 0,4 = > T = 0,8(s)\)
Tại thời điểm t = 0 , vật ở vị trí biên âm : \(x = - A = - 20(cm)\)
=> \(x = A\cos \varphi \) \( = > \cos \varphi = \frac{x}{A} = - 1 = > \varphi = \pi \)
b) Ta có chu kì dao động của vật : \(T = 0,8 = > \omega = \frac{{2\pi }}{{0,8}} = 2,5\pi (rad/s)\)
Vậy phương trình dao động : \(x = 20\cos \left( {2,5\pi t + \pi } \right)\)
c) Lúc t= 0,4 (s) vật đang ở vị trí biên dương : \(x = A = 20(cm)\)
Lúc t= 0,6 (s) vật đang ở VTCB : \(x = 0\)
Lúc t= 0,8 (s) vật đang ở vị trí biên âm : \(x = - A = - 20(cm)\)
2.9
Đồ thị li độ theo thời gian \({x_1},{x_2}\) của hai chất điểm dao động điều hoà được mô tả như Hình 2.2:
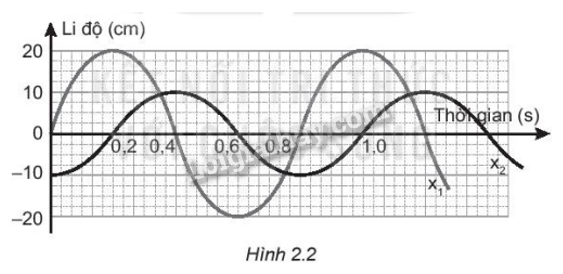
a) Xác định độ lệch pha của hai dao dao động.
b) Viết phương trình dao động của \({x_1},{x_2}\)
Phương pháp giải:
1. Vận dụng kiến thức đã học trong phần 1. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Đồ thị dao động điều hoà.
2. Độ lệch pha giữa hai dao động cùng chu kì
- Độ lệch pha là đại lượng không đổi, không phụ thuộc vào thời điểm quan sát
\({\varphi _1} > {\varphi _2}\)thì dao động 1 sớm pha hơn dao động 2
\({\varphi _1} < {\varphi _2}\)thì dao động 1 trễ pha hơn dao động 2
\({\varphi _1} = {\varphi _2}\)thì dao động 1 cùng (đồng) pha với dao động 2
\({\varphi _1} = {\varphi _2} + \varphi \) thì dao động 1 ngược pha với dao động 2
Lời giải chi tiết:
a) Từ đồ thị ta có :
Tại thời điểm t=0 , vật \({x_1}\) ở vị trí cân bằng \(x = 0\)
=> \({x_1} = {A_1}\cos {\varphi _1} < = > \cos {\varphi _1} = 0 = > {\varphi _1} = \frac{\pi }{2}\)
Biên độ dao động của \({x_2}\): \(A = x\max = 10(cm)\)
Tại thời điểm t=0 , vật \({x_2}\) ở vị trí biên âm \(x = - A\)
\( = > {x_2} = A\cos {\varphi _2} < = > \cos {\varphi _2} = - 1 = > {\varphi _2} = \pi \)
=> độ lệch pha của hai dao dao động \(\Delta \varphi = \ {{\varphi _2} - {\varphi _1}} \ = \frac{\pi }{2}\)
=> hai dao động vuông pha với nhau hoặc x1 sớm pha hơn x2 là \(\Delta \varphi = \frac{\pi }{2}\)
b) Từ đồ thị ta có :
Xét \({x_1}\)
Biên độ dao động của \({x_1}\) : \(A = x\max = 20(cm)\)
Từ vị trí thấp nhất đến vị trí cao nhất là \(\frac{T}{2} = 0,4 = > T = 0,8(s)\)\( = > \omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,8}} = 2,5\pi \)(rad/s)
Tại t = 0 vật có li độ x = 0 và đang chuyển động theo chiều dương nên \({\varphi _1} = - \frac{\pi }{2}\)
=> Phương trình dao động \({x_1} = 20\cos \left( {2,5\pi t - \frac{\pi }{2}} \right)\)
Xét \({x_2}\)
Biên độ dao động của \({x_2}\) : \(A = x\max = 10(cm)\)
Từ vị trí thấp nhất đến vị trí cao nhất là \(\frac{T}{2} = 0,4 = > T = 0,8(s)\)\( = > \omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,8}} = 2,5\pi \)(rad/s)
Tại t = 0 vật có li độ x = -10 cm và đang chuyển động theo chiều dương nên \({\varphi _2} = - {\pi }\)
=> Phương trình dao động \({x_2} = 10\cos \left( {2,5\pi t - \pi } \right)\)
2.10
Một chất điểm dao động điều hoà với chu khí T = 2s. trong 3 s vật đi được quãng đường 60 cm. Khi t = 0 vật đi qua vị trí cân bằng và hướng về vị trí biên dương. Hãy viết phương trình dao động của vật.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Chu kì: T là khoảng thời gian để vật thực hiện được một dao động.
Quãng đường trong một dao động \(S = 4A\)
Đồ thị dao động điều hoà.
Lời giải chi tiết:
Ta có chu kì dao động : \(T = 2s = > \omega = \frac{{2\pi }}{T} = \pi \left( {rad/s} \right)\)
Ta có : \(\frac{t}{T} = \frac{3}{2} = 1,5 = > t = 1,5T = T + \frac{T}{2}\) \( = > S = 4A + 2A = 6A = 60cm\) \( = > A = 10\left( {cm} \right)\)
Khi t = 0 vật đi qua vị trí cân bằng \(x\)\(x = 0\) và \(v > 0\)
\({x_1} = {A_1}\cos {\varphi _1} < = > \cos {\varphi _1} = 0 = > {\varphi _1} = - \frac{\pi }{2}\)
Vậy phương trình dao động của vật là : \(x = 10\cos \left( {\pi t - \frac{\pi }{2}} \right)\)
2.11
Một chất điểm dao động điều hoà theo phương trình \(x = 10\cos \left( {2\pi t + \frac{{5\pi }}{6}} \right)\left( {cm} \right)\). Tính quãng đường vật đi được trong khoảng thời gian từ t= 1 s đến t = 2,5 s.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Chu kì: T là khoảng thời gian để vật thực hiện được một dao động.
Quãng đường trong một dao động \(S = 4A\)
Lời giải chi tiết:
Từ phương trình ta có :
Biên độ dao động \(A = 10cm\)
Biên độ góc \(\omega = 2\pi = > T = \frac{{2\pi }}{\omega } = 1s\)
Khoảng thời gian từ t= 1 s đến t = 2,5 s \( = > \Delta t = 1,5s = 1,5T = T + \frac{T}{2}\)
=> Quãng đường vật đi được trong 1,5 T là \(S = 4A + 2A = 6A = 60cm\)
- Bài 3. Vận tốc, gia tốc trong dao động điều hòa trang 8, 9 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 5. Động năng. Thế năng. Sự chuyển hóa năng lượng trong dao động điều hòa trang 9, 10, 11, 12 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 6. Dao động tắt dần. Dao động cưỡng bức. Hiện tượng cộng hưởng trang 12, 13 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài ôn tập cuối chương I trang 14, 15, 16 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 1. Dao động điều hòa trang 4, 5 SBT Vật lí 11 Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Lí 11 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Bài tập cuối chương IV trang 64, 65, 66, 67 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 25. Năng lượng và công suất điện trang 61, 62, 63, 64 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 24. Nguồn điện trang 58, 59, 60, 61 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài tập cuối chương III trang 47, 48, 49 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 23. Điện trở. Định luật Ohm trang 53, 54, 55, 56, 57 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài tập cuối chương IV trang 64, 65, 66, 67 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 25. Năng lượng và công suất điện trang 61, 62, 63, 64 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 24. Nguồn điện trang 58, 59, 60, 61 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài tập cuối chương III trang 47, 48, 49 SBT Vật lí 11 Kết nối tri thức với cuộc sống
- Bài 23. Điện trở. Định luật Ohm trang 53, 54, 55, 56, 57 SBT Vật lí 11 Kết nối tri thức với cuộc sống













Danh sách bình luận