Giải bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều
Một doanh nghiệp dự định sản xuất các hộp dựng nước giải khát có dạng hình trụ với dung tích là 500 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\) (Hình 5). Hãy tính bán kính đáy và chiều cao của chiếc hộp để diện tích vỏ hộp là nhỏ nhất (Hình 6).
Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa
Đề bài
Một doanh nghiệp dự định sản xuất các hộp dựng nước giải khát có dạng hình trụ với dung tích là 500 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\) (Hình 5). Hãy tính bán kính đáy và chiều cao của chiếc hộp để diện tích vỏ hộp là nhỏ nhất (Hình 6).
Phương pháp giải - Xem chi tiết
+) Từ thể tích của hộp đựng nước giải khát ta sẽ biểu diễn được chiều cao của hộp nước theo bán kính đáy của nó \(h = \frac{{500}}{{\pi {r^2}}}\)
+) Diện tích vỏ hộp chính là diện tích toàn phần của hộp nước hình trụ.
+) Ta sẽ biểu diễn được diện tích vỏ hộp bằng một hàm số \(S(r)\)ẩn r
+) Yêu cầu bài toán đồng nghĩa với việc ta phải đi tìm bán kính, chiều cao mà ở đó hàm số \(S(r)\)đạt giá trị nhỏ nhất.
Lời giải chi tiết
Chiều cao \(h\) của hộp đứng nước có dạng hình trụ là \(h = \frac{{500}}{{\pi {r^2}}}\) (cm).
Diện tích mặt đáy của hộp đựng nước là \({S_{\rm{d}}} = \pi {r^2}\) (\({\rm{c}}{{\rm{m}}^{\rm{2}}}\)).
Diện tích xung quanh của hộp đựng nước là \({S_{xq}} = 2\pi rh = 2\pi r.\frac{{500}}{{\pi {r^2}}} = \frac{{1000}}{r}{\rm{(c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Diện tích vỏ hộp là \(S = 2\pi {r^2} + \frac{{1000}}{r}({\rm{c}}{{\rm{m}}^{\rm{2}}})\).
Xét hàm số \(S(r) = 2\pi {r^2} + \frac{{1000}}{r},r \in (0; + \infty ).\)
Ta có \(S'(r) = 4\pi r - \frac{{1000}}{{{r^2}}}.\) Do đó \(S'(r) = 0 \Leftrightarrow r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}.\)
Ta có bảng biến thiên của hàm số \(S(r)\) như sau:
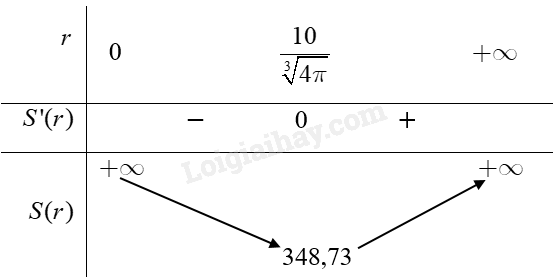
Căn cứ vào bảng biến thiên ta có \(\mathop {\min }\limits_{(0; + \infty )} S(r) \approx 348,73\) tại \(r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}\) (cm).
Vậy để diện tích vỏ hộp là nhỏ nhất thì bán kính của chiếc hộp là \(r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}\) (cm) và chiều cao của chiếc hộp là \(h = \frac{{500}}{{\pi {{\left( {\frac{{10}}{{\sqrt[3]{{4\pi }}}}} \right)}^2}}} = \frac{{5{{\left( {\sqrt[3]{{4\pi }}} \right)}^2}}}{\pi }\) (cm).
Bình luận
Chia sẻ
- Giải bài 9 trang 37 Chuyên đề học tập Toán 12 - Cánh diều
- Giải bài 7 trang 37 Chuyên đề học tập Toán 12 - Cánh diều
- Giải bài 6 trang 36 Chuyên đề học tập Toán 12 - Cánh diều
- Giải bài 5 trang 36 Chuyên đề học tập Toán 12 - Cánh diều
- Giải bài 4 trang 36 Chuyên đề học tập Toán 12 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Cánh diều - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
