Giải bài 6.40 trang 77 SGK Toán 8 - Cùng khám phá

Đề bài

Cho $\Delta ABC$ có $AD$ là đường trung tuyến. Một đường thẳng $d$ song song với $BC$ cắt $AB,AC$ và $AD$ lần lượt tại $M,N$ và $O$ .

a) Chứng minh rằng $O$ là trung điểm của $MN.$

b) Cho tỉ số của diện tích $\Delta AMN$ và $\Delta ABC$ là $\frac{4}{9}$ . Chứng minh rằng $O$ là trọng tâm của $\Delta ABC.$ 

Lời giải chi tiết

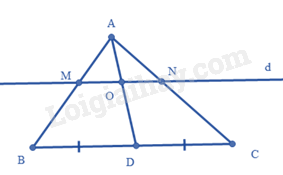
a) Xét tam giác $ABD$ và tam giác $AMO$ , ta có:

 $\frac{{AM}}{{AB}} = \frac{{AO}}{{AD}}$ (do $MO//BD$ áp dụng định lí Thales)

 $\widehat A$ là góc chung

=> $\Delta ABD$ ∽ $\Delta AMO$ (cạnh-góc-cạnh)

Ta có tỉ số đồng dạng:

 $\frac{{AM}}{{AB}} = \frac{{AO}}{{AD}} = \frac{{MO}}{{BD}}$ (1)

Chứng minh tương tự với tam giác $ANO$ và tam giác $ACD$ , ta được:

 $\Delta ANO$ ∽ $\Delta ACD$ (cạnh-góc-cạnh)

 $\frac{{AO}}{{AD}} = \frac{{AN}}{{AC}} = \frac{{ON}}{{DC}}$ (2)

Từ (1) và (2) suy ra:

 $\frac{{MO}}{{BD}} = \frac{{NO}}{{CD}} = \frac{{AO}}{{AD}}$

Mà $BD = CD$ (do $D$ là trung điểm)

=> $MO = NO$

=> O là trung điểm của $MN$ .

b)

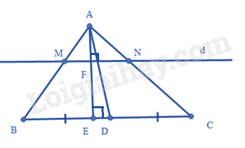
Kẻ đường cao $AE$ cắt $MN$ tại $F$ và cắt $BC$ tại $E$ .

Ta có $\Delta AMN$ ∽ $\Delta ABC$

=> $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{{AF}}{{AE}}$

Diện tích tam giác $AMN$ là: $\frac{1}{2}AF.MN$

Diện tích tam giác $ABC$ là: $\frac{1}{2}AE.BC$

Ta có tỉ số diện tích: $\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}AF.MN}}{{\frac{1}{2}AE.BC}} = \frac{4}{9}$

$\frac{{AF.MN}}{{AE.BC}} = \frac{4}{9}$

Mà $\frac{{AF}}{{AE}} = \frac{{MN}}{{BC}}$

=>

 $\begin{array}{l}\frac{{AF.MN}}{{AE.BC}} = \frac{4}{9}\\ \frac{{2AF}}{{2AE}} = \frac{4}{9}\\ \Rightarrow \frac{{AF}}{{AE}} = \frac{2}{3}\end{array}$

=> $\frac{{AO}}{{AD}} = \frac{2}{3}$

Vậy $O$ là trọng tâm của tam giác $ABC$