Giải bài 2.3 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức

Một nhà máy hóa chất sản xuất hai hợp chất X và Y. Khi sản xuất một đơn vị hợp chất X sẽ có 2 dm3 khí CO (carbon monoxide) và 6 dm3 khí SO2 (sulfur dioxide) phát tán ra môi trường. Khi sản xuất một đơn vị hợp chất Y sẽ có 4 dm3 khí CO và 3 dm3 khí SO2 phát tán ra môi trường. Các yêu cầu về khí thải chỉ cho phép nhà máy phát thải ra môi trường mỗi tuần không quá 3 000 dm3 khí CO và không quá 5 400 dm3 khí SO2. Nhà máy có thể bán hết tất cả các đơn vị hợp chất X và Y sản xuất ra với giá 36 000 đồn

Đề bài

Một nhà máy hóa chất sản xuất hai hợp chất X và Y. Khi sản xuất một đơn vị hợp chất X sẽ có 2 dm³ khí CO (carbon monoxide) và 6 dm³ khí SO₂ (sulfur dioxide) phát tán ra môi trường. Khi sản xuất một đơn vị hợp chất Y sẽ có 4 dm³ khí CO và 3 dm³ khí SO₂ phát tán ra môi trường. Các yêu cầu về khí thải chỉ cho phép nhà máy phát thải ra môi trường mỗi tuần không quá 3 000 dm³ khí CO và không quá 5 400 dm³ khí SO₂. Nhà máy có thể bán hết tất cả các đơn vị hợp chất X và Y sản xuất ra với giá 36 000 đồng một đơn vị hợp chất X và 24 000 đồng một đơn vị hợp chất Y. Xác định số đơn vị hợp chất X và Y mỗi loại cần sản xuất trong một tuần để thu được lợi nhuận cao nhất mà vẫn đảm bảo các yêu cầu về khí thải môi trường.

Phương pháp giải - Xem chi tiết

F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các điểm cực biên

Lời giải chi tiết

Gọi x và y lần lượt là số đơn vị hợp chất X và Y cần sản xuất.

Lợi nhuận thu được là: F(x; y) = 36 000x + 24 000y (đồng).

Ta có hệ bất phương trình sau:

\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\2{\rm{x}} + 4y \le 3{\rm{ }}000\\6{\rm{x}} + 3y \le {\rm{5 400}}\end{array} \right.\)

Miền nghiệm của hệ bất phương trình này là miền tứ giác OABC được tô màu như hình vẽ dưới đây:

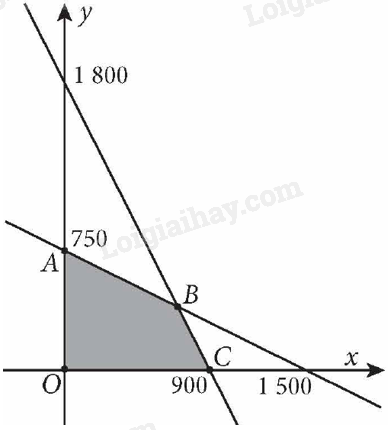
Các điểm cực biên là: O(0; 0), A(0; 750), B(700; 400), C(900; 0).

Ta có:

F(0; 0) = 36 000.0 + 24 000.0 = 0;

F(0; 750) = 36 000.0 + 24 000.750 = 18 000 000;

F(700; 400) = 36 000.700 + 24 000.400 = 34 800 000;

F(900; 0) = 36 000.900 + 24 000.0 = 32 400 000.

Giá trị lớn nhất của F(x; y) bằng 34 800 tại điểm cực biên B(700; 400).

Vậy cần sản xuất 700 đơn vị hợp chất X và 400 đơn vị hợp chất Y trong một tuần để thu được lợi nhuận cao nhất mà vẫn đảm bảo các yêu cầu về khí thải môi trường.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức
Chế độ ăn của một người yêu cầu mỗi ngày tối thiểu 400 đơn vị vitamin, 500 đơn vị khoáng chất và 1 400 đơn vị calo. Có hai loại thức ăn F1 và F2 mỗi đơn vị F1 giá 1 200 đồng và mỗi đơn vị F2 giá 720 đồng. Mỗi đơn vị thức ăn F1 chứa 2 đơn vị vitamin, 1 đơn vị khoáng chất và 4 đơn vị calo. Mỗi đơn vị thức ăn F2 chứa 1 đơn vị vitamin, 2 đơn vị khoáng chất và 4 đơn vị calo. Tìm chế độ hỗn hợp F1 và F2 sao cho chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng.
Giải bài 2.5 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức
Một hãng bán gà rán nghiên cứu thấy rằng để làm ra món gà rán có chất lượng tốt nhất thì thức ăn cho gà cần được bổ sung thêm 4 loại vitamin V1, V2, V3 và V4. Tổng lượng vitamin tối thiểu phải bổ sung cho mỗi 100 gam thức ăn cho gà là: V1 cần 50 đơn vị, V2 cần 100 đơn vị, V3 cần 60 đơn vị và V4 cần 180 đơn vị. Có hai loại thức ăn S1 và S2 cung cấp 4 loại vitamin này. Loại S1 có giá 720 đồng một gam và mỗi gam S1 có chứa 5 đơn vị V1, 25 đơn vị V2, 10 đơn vị V3 và 35 đơn vị V4. Loại S2 có giá 960
Giải bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức
Một cơ sở sản xuất hai loại sữa chua X và Y. Nguyên liệu chính để sản xuất hai loại sữa chua này dâu tây, sữa và đường. Để sản xuất một đơn vị sữa chua X và một đơn vị sữa chua Y cần lượng nguyên liệu như trong bảng: Nguồn nguyên liệu dự trữ dâu tây, sữa và đường lần lượt là 1,2 tấn; 0,8 tấn và 0,3 tấn. Giá bán mỗi đơn vị sữa chua X và Y lần lượt là 800 nghìn đồng và 1,2 triệu đồng. Cơ sở sản xuất cần sản xuất bao nhiêu đơn vị sữa chua X và Y để lợi nhuận thu được là lớn nhất?
Giải bài 2.1 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức
Một trung tâm tổ chức sự kiện có một phòng tổ chức lễ cưới với hai kiểu bàn ăn: bàn hình chữ nhật ngồi 6 người với giá thuê 200 nghìn đồng và bàn tròn ngồi 10 người với giá thuê 300 nghìn đồng. Anh Nam muốn thuê phòng để tổ chức đám cưới với 250 khách mời. Căn phòng chỉ chứa được tối đa 35 bàn các loại và chỉ có 15 bàn hình chữ nhật. Hỏi anh Nam phải thuê mỗi loại bàn bao nhiêu để giảm thiểu tối đa chi phí mà vẫn đáp ứng được các yêu cầu trên.
Giải mục 3 trang 29, 30, 31, 32 Chuyên đề học tập Toán 12 - Kết nối tri thức
Xét bài toán quy hoạch tuyến tính F(x; y) = 3x + 4y → min với các ràng buộc (left{ begin{array}{l}x ge 0,y ge 0\x + 2y ge 4\x + y ge 3end{array} right.) a) Kiểm tra lại rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán. b) Tìm tập hợp các điểm M(x; y) thoả mãn F(x; y) = 3x + 4y = 12. c) Với mỗi số thực m, xét đường thẳng dm: 3x + 4y = m. Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅. d) Từ phần c suy ra giá trị nhỏ nhất của F(x; y) trên miền chấp nhận
Giải mục 2 trang 26, 27, 28, 29 Chuyên đề học tập Toán 12 - Kết nối tri thức
Ta giải bài toán Tình huống mở đầu. Từ HĐ1 ta có bài toán quy hoạch tuyến tính sau: F(x; y) = 40x + 30y → max Với các ràng buộc (left{ begin{array}{l}x + 2y le 100\2x + y le 80\x ge 0,y ge 0end{array} right.) Miền chấp nhận được S của bài toán là miền tứ giác tô màu trong Hình 2.3. a) Tìm tập hợp các điểm M(x; y) thỏa mãn F(x; y) = 40x + 30y = 1 200. b) Với mỗi số thực m xét đường thẳng dm¬: 40x + 30y = m. Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅. c) Từ câu b suy ra gi
Giải mục 1 trang 24, 25, 26 Chuyên đề học tập Toán 12 - Kết nối tri thức
Trong bài toán mở đầu, gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất. a) Kí hiệu F(x; y) là lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II. Viết biểu thức tính F(x; y) theo x và y. b) Lập hệ bất phương trình bậc nhất hai ẩn ràng buộc x và y thỏa mãn yêu cầu của bài toán. c) Biểu diễn trên mặt phẳng toạ độ để thấy rằng miền nghiệm của hệ bất phương trình tìm được trong ý b là một miền tứ giác. Tìm toạ độ các đỉnh của miền tứ giác