 Đề thi toán 10, đề kiểm tra toán 10 chân trời sáng tạo có đáp án và lời giải chi tiết
Đề thi toán 10, đề kiểm tra toán 10 chân trời sáng tạo có đáp án và lời giải chi tiết
 Đề thi giữa kì 1 Toán 10 - Chân trời sáng tạo
Đề thi giữa kì 1 Toán 10 - Chân trời sáng tạo Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 1
Câu 1. Mệnh đề nào sau đây là phủ định của mệnh đề: “(exists x in mathbb{R}|{x^2} - 3x + 2 > 0)”
Đề bài
I. PHẦN TRẮC NGHIỆM
Câu 1. Mệnh đề nào sau đây là phủ định của mệnh đề: “\(\exists x \in \mathbb{R}|{x^2} - 3x + 2 > 0\)”
A. \(\exists x \in \mathbb{R}|{x^2} - 3x + 2 < 0\)
B. \(\exists x \in \mathbb{R}|{x^2} - 3x + 2 \le 0\)
C. \(\forall x \in \mathbb{R}|{x^2} - 3x + 2 \le 0\)
D. \(\forall x \in \mathbb{R}|{x^2} - 3x + 2 > 0\)
Câu 2. Cho tập hợp \(A = \{ 1;2;5;7;8\} \) và \(B = \{ x \in \mathbb{N}|x \le 3\} \). Tập hợp \(A \cap B\) là:
A. \(\{ 1;2\} \). B. \(\{ 1\} \). C. \(\{ 2\} \). D. \(\emptyset \)
Câu 3. Mỗi học sinh của lớp 10A đều thích môn Toán hoặc môn Tiếng Anh, biết rằng có 30 học sinh thích môn Toán, 25 học sinh thích môn Tiếng Anh và 15 em học sinh thích cả hai môn. Hỏi lớp 10A có tất cả bao nhiêu học sinh?
A. \(70\). B. \(60\). C. \(50\). D. \(40\).
Câu 4. Số tập hợp con của tập hợp A có 5 phần tử là :
A. \(20\). B. \(25\). C. \(32\) D. \(35\).
Câu 5. Cặp số nào sau đây là nghiệm của bất phương trình \(3(x - 1) + 4(y - 2) < 5x + 3\)
A. \((2;5)\). B. \(( - 2;3)\). C. \((0;6)\). D. \((4;5)\).
Câu 6. Miền nghiệm của bất phương trình \(x - 2y < 4\) là:
A. 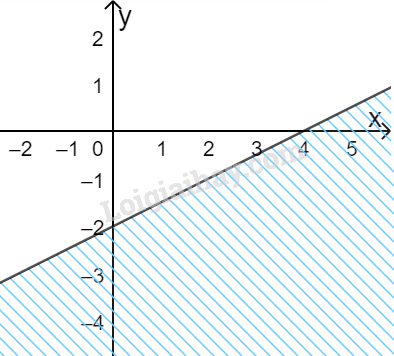 B.
B. 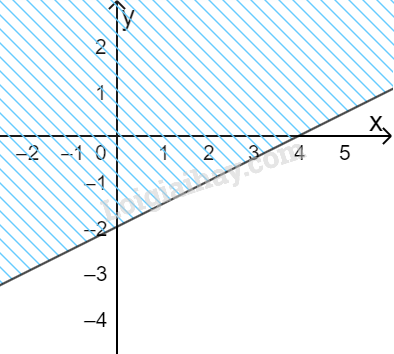
C. 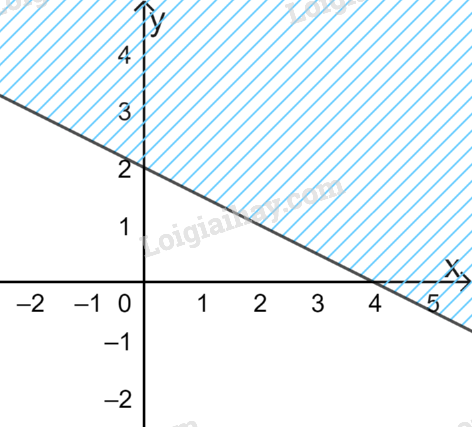 D.
D. 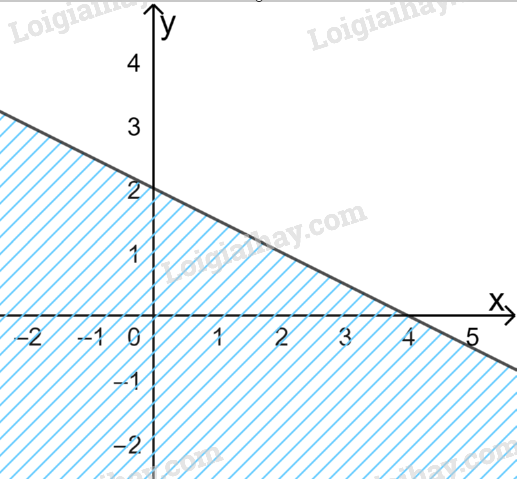
Câu 7. Giá trị nhỏ nhất của \(F(x;y) = x - 3y\), với điều kiện \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\)
A.\(2\) B. \( - 6\) C.\( - \frac{{34}}{3}\) D. \( - 15\)
Câu 8. Tập xác định của hàm số \(y = \frac{{x + 1}}{{{x^2} - 4}}\)
A. \(\mathbb{R}\). B. \(\mathbb{R}{\rm{\backslash }}\{ 2\} \) C. \(\mathbb{R}{\rm{\backslash }}\{ - 2;2\} \). D. \(\mathbb{R}{\rm{\backslash }}\{ - 2; - 1;2\} \).
Câu 9. Parabol \((P):y = {x^2} - 6x + 9\) có số điểm chung với trục hoành là
A.\(0\) B. \(1\). C. \(2\). D. \(3\).
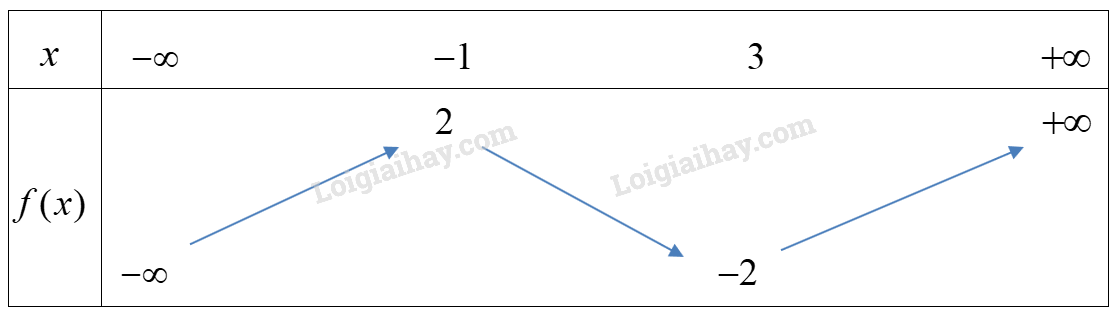
Câu 10. Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. \(f( - 3) > f( - 2)\) B. \(f(2) < f(\sqrt 5 )\)
C. \(f(1) < f(0)\) D. \(f(2020) > f(2022)\)
Câu 11. Đường thẳng nào dưới đây song song với đường thẳng \(y = \sqrt 3 x + 1\)
A. \(y = - \sqrt 3 x + 1\) B. \(y = \frac{{\sqrt 3 }}{3}x - 2\) C. \(y = \sqrt 3 x + 5\). D. \(y = \sqrt 3 - 5x\).
Câu 12. Cho hàm số \(f(x) = {x^2} - 4x + 10\). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(( - \infty ;2)\), đồng biến trên \((2; + \infty )\).
B. Hàm số nghịch biến trên \(\mathbb{R}\).
C. Hàm số nghịch biến trên \((2; + \infty )\), đồng biến trên \(( - \infty ;2)\).
D. Hàm số đồng biến trên \(\mathbb{R}\).
II. PHẦN TỰ LUẬN
Câu 1. Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - \infty ;1) \cap ( - 2; + \infty )\) b) \((3;7] \cup ( - 1;5]\) c) \(( - 4;7]{\rm{\backslash }}[2; + \infty )\)
Câu 2. Cô Lan dự định mua tối đa 210 bông hoa gồm hoa tươi và hoa sáp về bán ngày lễ. Biết số hoa tươi cần mua ít nhất là 50 bông, số hoa sáp tối đa là 100 bông và số hoa sáp chiếm ít nhất \(\frac{1}{3}\) tổng số hoa. Lợi nhuận trung bình là 4 nghìn với một bông hoa tươi và 3 nghìn cho một bông hoa sáp. Vậy cô Lan cần mua bao nhiêu hoa mỗi loại để lợi nhuận thu được là lớn nhất?
Câu 3.
a) Xác định parabol (P) biết \((P):y = a{x^2} + bx + 2\) đi qua A(1;0) và có trục đối xứng \(x = \frac{3}{2}\)
b) Xét sự biến thiên và vẽ đồ thị hàm số trên.
Lời giải chi tiết
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM
I. PHẦN TRẮC NGHIỆM
|
1. C |
2. A |
3. D |
4. C |
5. D |
6. A |
|
7. D |
8. C |
9. B |
10. C |
11. C |
12. A |
Câu 1:
Phương pháp:
Mệnh đề phủ định của mệnh đề “\(\exists x \in \mathbb{R}|P(x)\)” là “\(\forall x \in \mathbb{R}|\overline {P(x)} \)”
Cách giải:
Mệnh đề phủ định của mệnh đề: “\(\exists x \in \mathbb{R}|{x^2} - 3x + 2 > 0\)” là “\(\forall x \in \mathbb{R}|{x^2} - 3x + 2 \le 0\)”
Chọn C.
Câu 2:
Phương pháp:
Tập hợp \(A \cap B = \{ x \in A|x \in B\} \)
Cách giải:
\(A = \{ 1;2;5;7;8\} \) và \(B = \{ x \in \mathbb{N}|x \le 3\} = \{ 0;1;2;3\} \).
Tập hợp \(A \cap B = \{ 1;2\} \)
Chọn A.
Câu 3:
Phương pháp:
Gọi A là tập hợp các học sinh thích môn Toán của lớp 10A.
B là là tập hợp các học sinh thích môn Tiếng Anh của lớp 10A.
Cách giải:
Gọi A là tập hợp các học sinh thích môn Toán của lớp 10A.
B là là tập hợp các học sinh thích môn Tiếng Anh của lớp 10A.
Suy ra : \(A \cup B\) là tập hợp các học sinh thích môn Toán và Tiếng Anh (hay là tập hợp HS lớp 10A)
\(A \cap B\) là tập hợp các học sinh thích cả hai môn Toán và Tiếng Anh
Ta có : \(n(A) = 30;n(B) = 25;n(A \cap B) = 15\)
\( \Rightarrow \) Số học sinh lớp 10A là : \(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 30 + 25 - 15 = 40\)
Vậy lớp 10A có 40 học sinh.
Chọn D.
Câu 4:
Phương pháp:
Số tập hợp con của tập hợp A có n phần tử là : \({2^n}\)
Cách giải:
Số tập hợp con của tập hợp A có 5 phần tử là : \({2^5} = 32\)
Chọn C.
Câu 5:
Phương pháp:
Thay cặp số vào BPT, cặp số nào cho ta mệnh đề đúng thì cặp số đó là nghiệm của BPT đã cho.
Cách giải:
Xét bất phương trình :\(3(x - 1) + 4(y - 2) < 5x + 3\)
\(\begin{array}{l} \Leftrightarrow 3x - 3 + 4y - 8 - 5x - 3 < 0\\ \Leftrightarrow - 2x + 4y - 14 < 0\\ \Leftrightarrow x - 2y + 7 > 0\end{array}\)
Lần lượt thay các cặp số vào BPT, ta được:
+ \(2 - 2.5 + 7 = - 1 > 0\)sai nên \((2;5)\) không là nghiệm của bất phương trình
+ \( - 2 - 2.3 + 7 = - 1 > 0\) sai nên \(( - 2;3)\) không là nghiệm của bất phương trình
+ \(0 - 2.6 + 7 = - 5 > 0\) sai nên \((0;6)\) không là nghiệm của bất phương trình
+ \(4 - 2.5 + 7 = 1 > 0\) đúng nên \((4;5)\) là nghiệm của bất phương trình
Chọn D.
Câu 6:
Phương pháp:
Xác định đường thẳng \(x - 2y = 4\) và xét một điểm (không thuộc đường thẳng) xem có thuộc miền nghiệm hay không.
Cách giải:
Miền nghiệm của bất phương trình \(x - 2y < 4\) là:
Đường thẳng \(x - 2y = 4\) đi qua điểm có tọa độ (4;0) và (0; -2) => Loại C, D.
Xét điểm O(0;0), ta có: \(0 - 2.0 = 0 < 4\) nên O thuộc miền nghiệm.
Chọn A.
Câu 7:
Phương pháp:
Bước 1: Biểu diễn miền nghiệm, xác định các đỉnh của miền nghiệm
Bước 2: Thay tọa độ các đỉnh vào \(F(x;y) = x - 3y\), kết luận giá trị nhỏ nhất.
Cách giải:
Xét hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\)
Biểu diễn miền nghiệm của hệ, ta được
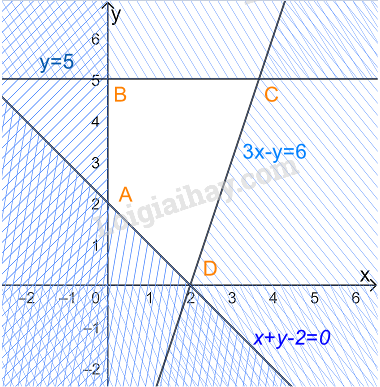
Miền nghiệm là miền tứ giác ABCD trong đó \(A\left( {0;2} \right),{\rm{ }}B\left( {0;5} \right),{\rm{ }}C\left( {\frac{{11}}{3};5} \right),D(2;0)\)
Thay tọa độ các điểm A, B, C, D vào \(F(x;y) = x - 3y\) ta được
\(F(0;2) = 0 - 3.2 = - 6\)
\(F(0;5) = 0 - 3.5 = - 15\)
\(F\left( {\frac{{11}}{3};5} \right) = \frac{{11}}{3} - 3.5 = - \frac{{34}}{3}\)
\(F(2;0) = 2 - 3.0 = 2\)
Vậy giá trị nhỏ nhất của F bằng -15.
Chọn D.
Câu 8:
Phương pháp:
\(\frac{{f(x)}}{{g(x)}}\) xác định khi \(g(x) \ne 0\)
Cách giải:
Hàm số \(y = \frac{{x + 1}}{{{x^2} - 4}}\) xác định khi \({x^2} - 4 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne - 2\end{array} \right.\)
Tập xác định là \(\mathbb{R}{\rm{\backslash }}\{ - 2;2\} \)
Chọn C.
Câu 9:
Phương pháp:
Số giao điểm của Parabol \((P):y = f(x)\) với trục hoành là số nghiệm của phương trình \(f(x) = 0\).
Cách giải:
Xét phương trình hoành độ giao điểm của (P) với trục hoành là:
\(\begin{array}{l}{x^2} - 6x + 9 = 0\\ \Leftrightarrow {\left( {x - 3} \right)^2} = 0\\ \Leftrightarrow x - 3 = 0\\ \Leftrightarrow x = 3\end{array}\)
PT có nghiệm duy nhất \(x = 3\) nên parabol có đúng 1 điểm chung với trục hoành
Chọn B.
Câu 10:
Cách giải:
Từ bảng biến thiên ta suy ra
Hàm số đồng biến trên \(( - \infty ; - 1)\) và \((3; + \infty )\)
Hàm số nghịch biến trên \(( - 1;3)\)
+ Vì \( - 3, - 2 \in ( - \infty ; - 1)\) và \( - 3 < - 2\) nên \(f( - 3) < f( - 2)\) => A sai.
+ Vì \(2,\sqrt 5 \in ( - 1;3)\) và \(2 < \sqrt 5 \) nên \(f(2) > f(\sqrt 5 )\) => B sai.
+ Vì \(0,1 \in ( - 1;3)\) và \(0 < 1\) nên \(f(0) > f(1)\) => C đúng.
+ Vì \(2000,2022 \in (3; + \infty )\) và \(2000 < 2022\) nên \(f(2020) < f(2022)\) => D sai.
Chọn C.
Câu 11:
Phương pháp:
Đường thẳng song song với đường thẳng \(y = ax + b\) có dạng \(y = ax + b'\) với \(b \ne b'\)
Cách giải:
Đường thẳng song song với đường thẳng \(y = \sqrt 3 x + 1\) có dạng \(y = \sqrt 3 x + b'\) với \(b' \ne 1\)
Chọn C.
Câu 12:
Cách giải:
Xét hàm số \(f(x) = {x^2} - 4x + 10\), có \(a = 1 > 0,b = - 4,c = 10\)
\( \Rightarrow \frac{{ - b}}{{2a}} = 2;\frac{{ - \Delta }}{{4a}} = \frac{{ - {{( - 4)}^2} + 4.1.10}}{4} = 6\)
Bảng biến thiên:
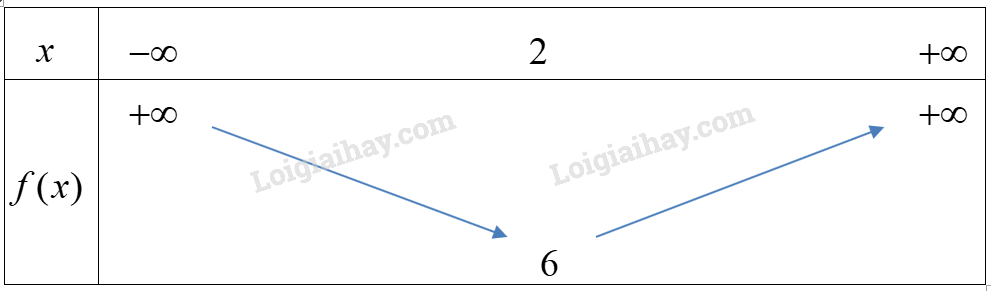
Hàm số đồng biến trên \((2; + \infty )\) và nghịch biến trên \(( - \infty ;2)\).
Chọn A.
II. PHẦN TỰ LUẬN
Câu 1 (TH):
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Biểu diễn hai tập \(( - \infty ;1)\) và \(( - 2; + \infty )\) trên trục số, ta được:
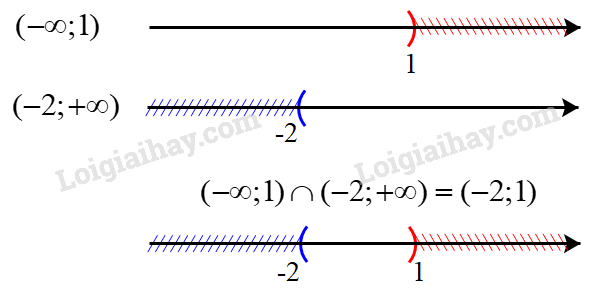
Giao của hai tập hợp: \(( - \infty ;1) \cap ( - 2; + \infty ) = ( - 2;1)\)
b) Biểu diễn hai tập \((3;7]\) và \(( - 1;5]\) trên trục số, ta được:
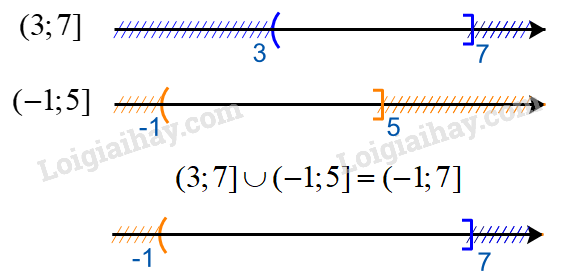
Hợp của hai tập hợp: \((3;7] \cup ( - 1;5] = ( - 1;7]\)
c) Biểu diễn hai tập \(( - 4;7]\) và \([2; + \infty )\) trên trục số, ta được:
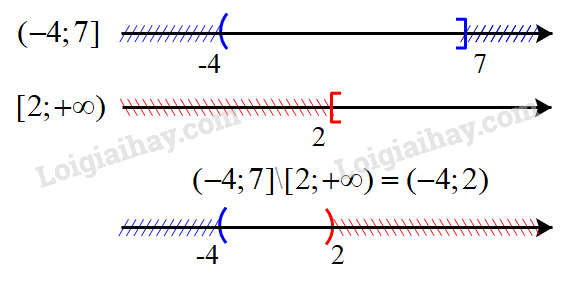
Hiệu của hai tập hợp: \(( - 4;7]{\rm{\backslash }}[2; + \infty ) = ( - 4;2)\)
Câu 2 (VD):
Cách giải:
Gọi số hoa tươi và hoa sáp cần mua lần lượt là x, y (bông). \((x,y \in \mathbb{N})\)
Mua tối đa 210 bông nên ta có: \(x + y \le 210\)
Số hoa tươi cần mua ít nhất là 50 bông, số hoa sáp tối đa là 100 bông hay \(x \ge 50;0 \le y \le 100\)
Số hoa sáp chiếm ít nhất \(\frac{1}{3}\) tổng số hoa nên \(y \ge \frac{1}{3}(x + y)\) hay \(x - 2y \le 0\)
Lợi nhuận thu được là: \(F(x;y) = 4x + 3y\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}x \ge 50\\0 \le y \le 100\\x + y \le 210\\x - 2y \le 0\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:

Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(50;25),B(50;100),C(110;100),D(140;70)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 4x + 3y\) ta được:
\(\begin{array}{l}F(50;25) = 4.50 + 3.25 = 275\\F(50;100) = 4.50 + 3.100 = 500\\F(110;100) = 4.110 + 3.100 = 740\\F(140;70) = 4.140 + 3.70 = 770\end{array}\)
Do đó F đạt giá trị lớn nhất bằng 770 tại \(x = 140;y = 70\)
Vậy cô Lan cần mua 140 bông hoa tươi và 70 bông hoa sáp.
Câu 3:
Cách giải:
a) Parabol \((P):y = a{x^2} + bx + 2\) đi qua A(1;0) nên \(0 = a{.1^2} + b.1 + 2 \Leftrightarrow a + b = - 2\)
Lại có: (P) có trục đối xứng \(x = - \frac{b}{{2a}} = \frac{3}{2}\)\( \Rightarrow 3a = - b\)
Từ đây ta tìm được \(a = 1,b = - 3\)
Vậy parabol đó là \((P):y = {x^2} - 3x + 2\)
b) Parabol \((P):y = {x^2} - 3x + 2\) có \(a = 1 > 0,b = - 3\)
Bảng biến thiên
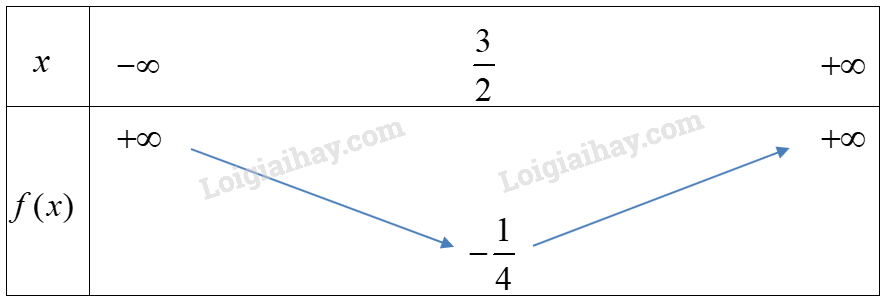
Hàm số đồng biến trên \((\frac{3}{2}; + \infty )\) và nghịch biến trên \(( - \infty ;\frac{3}{2})\).
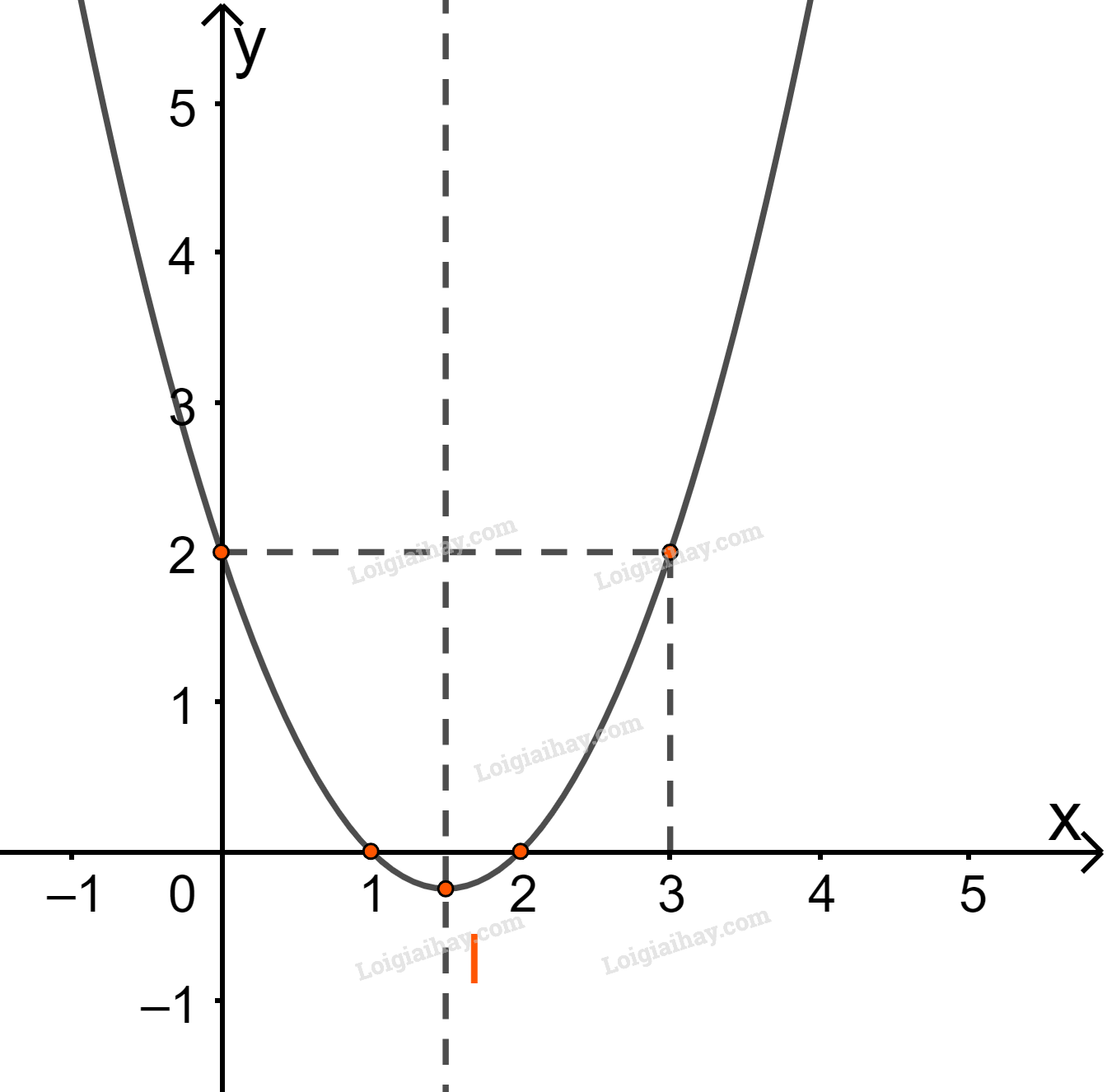
+ Vẽ đồ thị
Đỉnh \(I(\frac{3}{2};2)\)
(P) giao Ox tại \(A\left( {1;0} \right)\) và \(B(2;0)\)
(P) giao Oy tại điểm C(0;2)
Điểm D(3;2) đối xứng với C(0;2) qua trục đối xứng.
- Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 2
- Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 3
- Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 4
- Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 5
- Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 6
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục












Danh sách bình luận