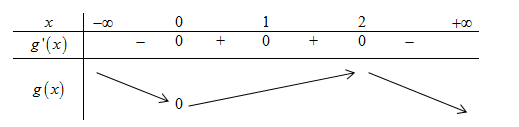Câu hỏi
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) có \(f\left( 0 \right) = 0\) và đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên. Hàm số \(y = \left| {3f\left( x \right) - {x^3}} \right|\)đồng biến trên khoảng
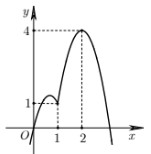
- A \(\left( {2;\, + \infty } \right)\)
- B \(\left( { - \infty ;2} \right)\)
- C \(\left( {0;2} \right)\)
- D \(\left( {1;3} \right)\)
Phương pháp giải:
+) Đặt \(y = g\left( x \right) = 3f\left( x \right) - {x^2}\), lập BBT của đồ thị hàm số \(y = g\left( x \right)\).
+) Từ đồ thị hàm số \(y = g\left( x \right)\) suy ra đồ thị hàm số \(y = \left| {g\left( x \right)} \right|\) và kết luận các khoảng đơn điệu của hàm số
Lời giải chi tiết:
Xét hàm số \(y = g\left( x \right) = 3f\left( x \right) - {x^3}\) ta có \(g'\left( x \right) = 3f'\left( x \right) - 3{x^2} = 0 \Leftrightarrow f'\left( x \right) = {x^2}\,\,\left( * \right)\).
Vẽ đồ thị hàm số \(y = {x^2}\) trên cùng mặt phẳng tọa độ với đồ thị hàm số \(y = f'\left( x \right)\) ta được:
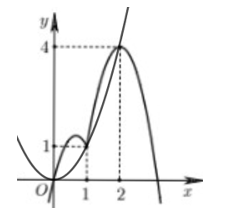
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đồ thị hàm số \(y = {x^2}\).
Dựa vào đồ thị hàm số ta thấy \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 2\end{array} \right.\).
BBT:
Do \(f\left( 0 \right) = 0 \Rightarrow g\left( 0 \right) = 3f\left( 0 \right) - {0^2} = 0\).
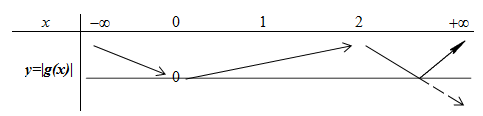
Từ đó ta suy ra BBT của đồ thị hàm số \(y = \left| {g\left( x \right)} \right|\) như sau:
Dựa vào BBT ta thấy hàm số \(y = \left| {g\left( x \right)} \right|\) đồng biến trên \(\left( {0;2} \right)\) và \(\left( {{x_0}; + \infty } \right)\) với \({x_0} > 2\).
Chọn C.