Phương pháp giải:

Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình nón đã cho.

Lời giải chi tiết:

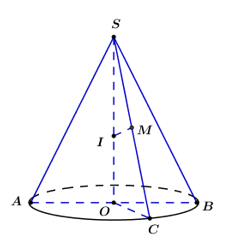
Gọi \(SC\) là một đường sinh của hình nón.

Khi đó xác định đường kính mặt cầu ngoại tiếp hình nón chính là ta cần tìm đường kính mặt cầu ngoại tiếp hình chóp \(SABC.\)

Ta có: \(SO\) là trục của hình chóp \(SABC.\)

Dựng đường thẳng trung trực của \(SC,\) cắt \(SO\) tại \(I \Rightarrow I\) là tâm mặt cầu cần tìm, bán kính là \(R = SI.\)

Ta có: \(\Delta SMI \sim \Delta SOC\,\,\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{SM}}{{SO}} = \dfrac{{SI}}{{SC}} \Leftrightarrow \dfrac{1}{1} = \dfrac{{SI}}{2} \Leftrightarrow SI = 2.\)

\( \Rightarrow \)Đường kính mặt cầu cần tìm là: \(d = 2SI = 4.\)  

Chọn A.