Câu hỏi
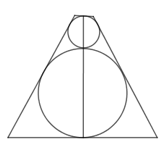
Người ta sản xuất một vật lưu niệm \(\left( N \right)\) bằng thủy tinh trong suốt có dạng khối tròn xoay mà thiết diện qua trục của nó là một hình thang cân (xem hình vẽ). Bên trong \(\left( N \right)\) có hai khối cầu ngũ sắc với bán kính lần lượt là \(R = 3cm,\,\,r = 1cm\) tiếp xúc với nhau và cùng tiếp xúc với mặt xung quanh của \(\left( N \right)\), đồng thời tiếp xúc với hai mặt đáy của \(\left( N \right)\). Tính thể tích của vật lưu niệm đó.
- A \(\dfrac{{485\pi }}{6}\left( {c{m^3}} \right)\)
- B \(81\pi \left( {c{m^3}} \right)\)
- C \(72\pi \left( {c{m^3}} \right)\)
- D \(\dfrac{{728\pi }}{9}\left( {c{m^3}} \right)\)
Phương pháp giải:
Sử dụng công thức tính thể tích khối nón cụt \(V = \dfrac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\) trong đó \(h\) là chiều cao của khối nón, \(R,\,\,r\) lần lượt là 2 bán kính đáy của nón cụt.
Lời giải chi tiết:
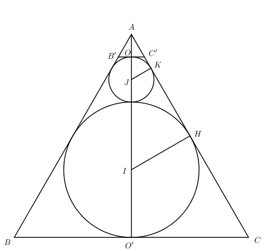
Gọi \(I,\,\,J\) lần lượt là tâm hai khối cầu, \(O;\,\,O'\) lần lượt là tâm 2 mặt đáy của khối \(\left( N \right)\).
Gọi \(H,\,\,K\) là hai tiếp điểm của hai khối cầu và hai mặt bên của khối \(\left( N \right)\) như hình vẽ ta có \(IH//JK\).
Dễ dàng nhận thấy:
\(\Delta AJK \sim \Delta AIH\,\,\left( {g.g} \right) \Rightarrow \dfrac{{AJ}}{{AI}} = \dfrac{{JK}}{{IH}} = \dfrac{1}{3} \Rightarrow AJ = \dfrac{1}{2}IJ = \dfrac{1}{2}.\left( {1 + 3} \right) = 2\)
\( \Rightarrow AO = AJ - OJ = 2 - 1 = 1\).
\( \Rightarrow AO' = 1 + 2 + 6 = 9 = h\).
Lại có \(\Delta AJK \sim \Delta ACO' \Rightarrow \dfrac{{JK}}{{O'C}} = \dfrac{{AJ}}{{AC}}\)
\(\begin{array}{l} \Rightarrow O'C = \dfrac{{JK.AC}}{{AJ}} = \dfrac{{1.\sqrt {{9^2} + O'{C^2}} }}{2} \Leftrightarrow 4O'{C^2} = {9^2} + O'{C^2}\\ \Leftrightarrow 3O'{C^2} = 81 \Leftrightarrow O'{C^2} = 27 \Leftrightarrow O'C = 3\sqrt 3 = R\end{array}\).
\(\Delta AOC' \sim \Delta AO'C\,\,\left( {g.g} \right) \Rightarrow \dfrac{{OC'}}{{O'C}} = \dfrac{{AO}}{{AO'}} = \dfrac{1}{9} \Leftrightarrow OC' = \dfrac{1}{9}O'C = \dfrac{{\sqrt 3 }}{3} = r\).
Vậy thể tích khối nón cụt là \(V = \dfrac{1}{3}\pi \left( {{R^2} + {r^2} + Rr} \right)h = \dfrac{1}{3}\pi \left( {27 + \dfrac{1}{3} + 3\sqrt 3 .\dfrac{{\sqrt 3 }}{3}} \right).8 = \dfrac{{728\pi }}{9}\,\,\left( {c{m^3}} \right)\).
Chọn D.