Câu hỏi
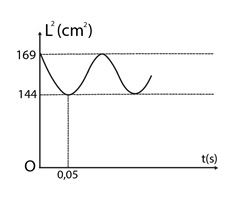
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là điểm bụng gần A nhất. Gọi L là khoảng cách giữa A và B ở thời điểm t. Biết rằng giá trị của L2 phụ thuộc vào thời gian được mô tả bởi đồ thị như hình bên. Điểm N trên dây có vị trí cân bằng là trung điểm của AB khi dây duỗi thẳng. Gia tốc dao động của N có giá trị lớn nhất bằng
- A 5π2 m/s2
- B 2,5π2 m/s2
- C \(2,5\sqrt{2}{{\pi }^{2}}\) m/s2
- D \(10\sqrt{2}{{\pi }^{2}}\)m/s2
Phương pháp giải:
Khoảng cách giữa nít và bụng sóng liền kề trong sóng dừng là λ/4
Biên độ dao động của điểm cách nút sóng gần nhất đoạn d là \({{a}_{N}}=\left| {{A}_{b}}\text{cos}\frac{2\pi d}{\lambda } \right|\)
Thời gian ngắn nhất để điểm B ở VTCBđến khi tới biên là T/4
Gia tốc lớn nhất của dao động : amax = ω2A
Liên hệ giữa tần số góc và chu kỳ dao động điều hòa : \(\omega =\frac{2\pi }{T}\)
Lời giải chi tiết:
Vì A là điểm nút nên uA = 0
Khoảng cách ngắn nhất giữa A và B là khi điểm B dao động qua VTCB.
Khi đó \(AB=\frac{\lambda }{4}=\sqrt{144}=12cm\Rightarrow \lambda =48cm\) ở thời điểm t = 0,05s
Khoảng cách lớn nhất giữa A và B là khi B dao động cực đại (là điểm bụng). Khi đó :
\(AB=\sqrt{{{\left( \frac{\lambda }{4} \right)}^{2}}+{{A}^{2}}}=\sqrt{169}=13cm\)
=> Biên độ dao động ở bụng sóng : A = 5cm
N có vị trí cân bằng là trung điểm AB nên vị trí cân bằng của N cách A đoạn d = AB/2 = 6cm
Biên độ dao động tại N là : \({{a}_{N}}=\left| {{A}_{b}}\text{cos}\frac{2\pi d}{\lambda } \right|=\left| \text{5cos}\frac{2\pi 6}{48} \right|=2,5\sqrt{2}cm\)
Thời gian ngắn nhất từ lúc điểm B ở VTCB đến khi tới biên là T/4 = 0,05s => T = 0,2s
Tần số góc của dao động \(\omega =\frac{2\pi }{T}=10\pi rad/s\)
Gia tốc lớn nhất của N là amax = ω2aN = \({{10}^{2}}{{\pi }^{2}}.2,5\sqrt{2}=250{{\pi }^{2}}\sqrt{2}cm/{{s}^{2}}=2,5{{\pi }^{2}}\sqrt{2}m/{{s}^{2}}\)
Chọn C