Câu hỏi
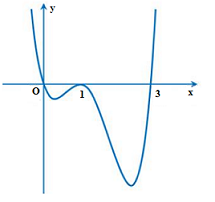
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) trên tập số thực \(\mathbb{R}\) và đồ thị của hàm số \(y = f\left( x \right)\) như hình vẽ. Khi đó, đồ thị của hàm số \(y = {\left( {f\left( x \right)} \right)^2}\) có
- A \(2\) điểm cực đại, \(2\) điểm cực tiểu
- B
\(2\) điểm cực tiểu, \(3\) điểm cực đại
- C \(1\) điểm cực đại, \(3\) điểm cực tiểu
- D \(2\) điểm cực đại, \(3\) điểm cực tiểu
Phương pháp giải:
+ Từ đồ thị của hàm \(y = f\left( x \right)\) ta suy ra các điểm mà tại đó \(f\left( x \right) = 0\) (các giao điểm với trục hoành) và các điểm là cho \(f'\left( x \right) = 0\) (chính là các điểm cực trị của hàm số \(y = f\left( x \right)\) )
+ Sử dụng đạo hàm hàm hợp \({\left( {u\left( x \right)} \right)^2} = 2u\left( x \right).u'\left( x \right)\)
+ Lập bảng xét dấu của hàm \(y = {\left( {f\left( x \right)} \right)^2}\)
+ Từ đó xác định các điểm cực đại và điểm cực tiểu.
- Nếu \(y'\) đổi dấu từ âm sang dương tại \({x_0}\) thì \({x_0}\) là điểm cực tiểu của hàm số
- Nếu \(y'\) đổi dấu từ dương sang âm tại \({x_0}\) thì \({x_0}\) là điểm cực đại của hàm số
Lời giải chi tiết:
Từ đồ thị hàm số \(f\left( x \right)\) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \(x = 0;x = 1;x = 3\) nên \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 3\end{array} \right.\).
Lại thấy đồ thị hàm số \(y = f\left( x \right)\) có ba điểm cực trị nên \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = {x_1} \in \left( {0;1} \right)\\x = {x_2} \in \left( {1;3} \right)\end{array} \right.\)
Hàm số \(y = {\left( {f\left( x \right)} \right)^2}\) có đạo hàm \(y' = 2f\left( x \right).f'\left( x \right)\)
Xét phương trình \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f'\left( x \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 3\\x = {x_1}\\x = {x_2}\end{array} \right.\)
Ta có BXD của \(y'\) như sau

Nhận thấy hàm số \(y = {\left( {f\left( x \right)} \right)^2}\) có \(y'\) đổi dấu từ âm sang dương tại ba điểm \(x = 0;x = 1;x = 3\) nên hàm số có ba điểm cực tiểu. Và \(y'\) đối dấu từ dương sang âm tại hai điểm \(x = {x_1};x = {x_2}\) nên hàm số có hai điểm cực đại.
Chọn D.







