Câu hỏi
Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ góc α0 nhỏ. Lấy mốc thế năng ở vị trí cân bằng, khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng thì li độ góc α của con lắc bằng:
- A \( - \frac{{{\alpha _0}}}{{\sqrt 3 }}\)
- B \( - \frac{{{\alpha _0}}}{{\sqrt 2 }}\)
- C \(\frac{{{\alpha _0}}}{{\sqrt 2 }}\)
- D \(\frac{{{\alpha _0}}}{{\sqrt 3 }}\)
Phương pháp giải:
Phương pháp:
+ Sử dụng công thức tính thế năng và cơ năng của con lắc đơn: \({{\rm{W}}_t} = \frac{1}{2}mgl{\alpha ^2};{{\rm{W}}_{\rm{d}}} = \frac{1}{2}mgl{\alpha _0}^2\)
+ Áp dụng công thức tính cơ năng dao động: \({\rm{W}} = {{\rm{W}}_{\rm{d}}} + {{\rm{W}}_t}\)
+ Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
Hướng dẫn giải:
Ta có: Thế năng và cơ năng của con lắc: \({{\rm{W}}_t} = \frac{1}{2}mgl{\alpha ^2};{{\rm{W}}_{\rm{d}}} = \frac{1}{2}mgl{\alpha _0}^2\)
Khi \({{\rm{W}}_{\rm{d}}} = {{\rm{W}}_t} \to {\rm{W}} = {{\rm{W}}_{\rm{d}}} + {{\rm{W}}_t} = 2{{\rm{W}}_t} \leftrightarrow \frac{1}{2}mgl{\alpha _0}^2 = 2.\frac{1}{2}mgl{\alpha ^2} \to \alpha = \pm \frac{{{\alpha _0}}}{{\sqrt 2 }}\)
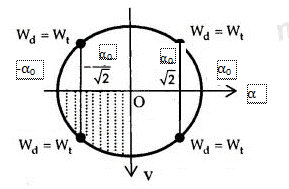
Con lắc chuyển động nhanh dần theo chiều dương khi con lắc chuyển động từ biên âm về VTCB theo chiều dương (vùng 3) => \(\alpha = - \frac{{{\alpha _0}}}{{\sqrt 2 }}\)
=> Chọn B







