Câu hỏi
Cho tứ diện \(ABCD\) có \(AC = AD = BC = BD = a,\,\,\left( {ACD} \right) \bot \left( {BCD} \right)\) và \(\left( {ABC} \right) \bot \left( {ABD} \right)\). Tính độ dài cạnh \(CD\).
- A \(\frac{{2\sqrt 3 }}{3}a\)
- B \(2\sqrt 2 a\)
- C \(\sqrt 2 a\)
- D \(\frac{{\sqrt 3 }}{3}a\)
Phương pháp giải:
+) Gọi \(M,N\) lần lượt là trung điểm của \(CD,AB\). Chứng minh \(\Delta CDN\) và \(ABM\) vuông cân và \(MN \bot AB,\,\,\,MN \bot CD\).
+) Đặt \(CD=x.\) Áp dụng định lí Pytago tính \(x\).
Lời giải chi tiết:
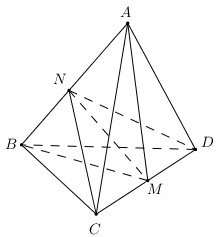
Gọi \(M,N\) lần lượt là trung điểm của \(CD,AB\).
\(\Delta ACD\) và \(\Delta BCD\) cân \( \Rightarrow AM \bot CD,\,\,BM \bot CD\).
Ta có :
\(\left\{ \begin{array}{l}
\left( {ACD} \right) \cap \left( {BCD} \right) = CD\\
\left( {ACD} \right) \supset AM \bot CD\\
\left( {BCD} \right) \supset BM \bot CD
\end{array} \right. \Rightarrow \angle \left( {\left( {ACD} \right);\left( {BCD} \right)} \right) = \angle \left( {AM;BM} \right) = {90^0}\)
\( \Rightarrow AM \bot BM\)
Và ta dễ dàng chứng minh được \(\Delta ACD=\Delta BC\,\,\left( c.c.c \right)\Rightarrow AM=BM\).
\( \Rightarrow \Delta ABM\) vuông cân tại \(M\Rightarrow MN\bot AB\).
Chứng minh tương tự ta có \(\Delta CDN\) vuông cân tại \(N\) và \(MN\bot CD\).
Đặt \(CD=x\). Áp dụng định lí Pytago ta có: \(A{M^2} = {a^2} - \dfrac{{{x^2}}}{4}\).
\(\Delta ABM\) vuông cân tại \(M\Rightarrow A{{B}^{2}}=2A{{M}^{2}}=2{{a}^{2}}-\dfrac{{{x}^{2}}}{2}\Rightarrow A{{N}^{2}}=\dfrac{1}{4}A{{B}^{2}}=\dfrac{{{a}^{2}}}{2}-\dfrac{{{x}^{2}}}{8}\).
Áp dụng định lí Pytago ta có: \(D{{N}^{2}}=A{{D}^{2}}-A{{N}^{2}}={{a}^{2}}-\dfrac{{{a}^{2}}}{2}+\dfrac{{{x}^{2}}}{8}=\dfrac{{{a}^{2}}}{2}+\dfrac{{{x}^{2}}}{8}\)
\(\Delta CDN\) vuông cân tại \(N\Rightarrow C{{D}^{2}}=2D{{N}^{2}}={{a}^{2}}+\dfrac{{{x}^{2}}}{4}={{x}^{2}}\Leftrightarrow x=\dfrac{2\sqrt{3}a}{3}\)
Chọn A.







