Câu hỏi
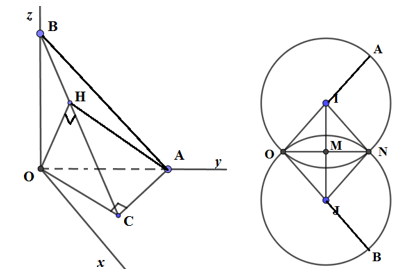
Trong không gian \(Oxyz\), cho các điểm \(A\left( {0;4\sqrt 2 ;0} \right),\,\,B\left( {0;0;4\sqrt 2 } \right)\), điểm \(C \in mp\left( {Oxy} \right)\) và tam giác \(OAC\) vuông tại \(C\); hình chiếu vuông góc của \(O\) trên \(BC\) là điểm \(H\). Khi đó điểm \(H\) luôn thuộc đường tròn cố định có bán kính bằng:
- A \(2\sqrt 2 \)
- B \(4\)
- C \(\sqrt 3 \)
- D \(2\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}AC \bot OC\\AC \bot OB\end{array} \right.\,\, \Rightarrow AC \bot \left( {OBC} \right) \Rightarrow AC \bot OH\)
Mà \(OH \bot BC \Rightarrow OH \bot \left( {ABC} \right) \Rightarrow OH \bot AH \Rightarrow H\) di động trên mặt cầu đường kính OA.
Mặt khác \(OH \bot BH \Rightarrow H\) di động trên mặt cầu đường kính OB.
\( \Rightarrow H\) di động trên đường tròn cố định là giao tuyến của hai mặt cầu trên (mặt cầu đường kính OA và mặt cầu đường kính OB)
Bán kính cần tìm là: \(r = OM = \dfrac{{OI}}{{\sqrt 2 }} = \dfrac{{\dfrac{{4\sqrt 2 }}{2}}}{{\sqrt 2 }} = 2\) (do tam giác OIM vuông cân tại M)
Chọn: D