Phương pháp giải:

Thể tích khối trụ là: \(V = \pi {r^2}h\).

Diện tích toàn phần của hình trụ: \({S_{tp}} = 2\pi {r^2} + 2\pi rh\).

Lời giải chi tiết:

Ta có: \(V = \pi {r^2}h \Leftrightarrow h = \dfrac{V}{{\pi {r^2}}}\)

Diện tích vật liệu để làm vỏ hộp là: \({S_{tp}} = 2\pi {r^2} + 2\pi rh = 2\pi {r^2} + 2\pi r.\dfrac{V}{{\pi {r^2}}} = 2\pi {r^2} + \dfrac{{2V}}{r} = f\left( r \right)\), \(r > 0\)

Ta có :  \(f'\left( r \right) = 4\pi r - \dfrac{{2V}}{{{r^2}}},\,\,f'\left( r \right) = 0 \Leftrightarrow {r^3} = \dfrac{V}{{2\pi }} \Leftrightarrow r = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\)

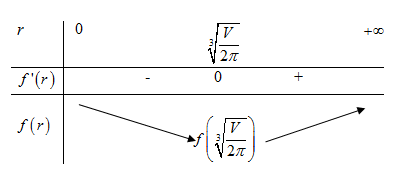
Bảng biến thiên:

Vậy, để tiết kiệm vật liệu nhất thì bán kính đáy phải bằng \(\sqrt[3]{{\dfrac{V}{{2\pi }}}}\).

Chọn A.