Câu hỏi
Cần phải làm cái cửa sổ mà phía trên là hình bán nguyệt, phía dưới là hình chữ nhật, có chu vi là a mét (a chính là chu vi hình bán nguyệt cộng với chu vi hình chữ nhật trừ đi đường kính của hình bán nguyệt). Gọi d là đường kính của hình bán nguyệt. Hãy xác định d để diện tích cửa sổ là lớn nhất.
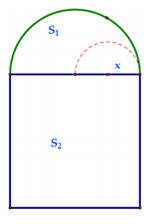
- A \(d = \dfrac{a}{{4 + \pi }}\).
- B \(d = \dfrac{{2a}}{{4 + \pi }}\)
- C \(d = \dfrac{a}{{2 + \pi }}\).
- D \(d = \dfrac{{2a}}{{2 + \pi }}\).
Phương pháp giải:
+) Gọi bán kính hình bán nguyệt là \(x\) , xác định độ dài các cạnh hình chữ nhật theo \(a,\,x\).
+) Tính diện tích cửa số, sử dụng phương pháp khảo sát hàm số để tìm GTLN của hàm diện tích.
Lời giải chi tiết:
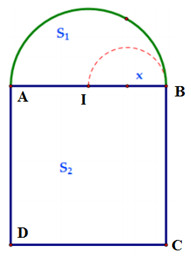
Gọi độ dài đoạn IB là x mét. Khi đó: độ dài hình bán nguyệt là \(\pi x\) (mét).
Ta có \(AB = 2x,\,\,\)\(BC = \dfrac{{a - \pi x - 2x}}{2}\)\( = \dfrac{{a - \left( {\pi + 2} \right)x}}{2}\)
Diện tích cửa số:
\(\begin{array}{l}S = {S_1} + {S_2} = \dfrac{1}{2}\pi {x^2} + 2x.\dfrac{{a - \left( {\pi + 2} \right)x}}{2}\\\,\,\,\, = \dfrac{1}{2}\pi {x^2} + ax - \left( {\pi + 2} \right){x^2} = - \dfrac{{\left( {\pi + 4} \right){x^2}}}{2} + ax\end{array}\)
Xét hàm số \(f\left( x \right) = - \dfrac{{\left( {\pi + 4} \right){x^2}}}{2} + ax,\,\,\left( {x > 0} \right)\) có \(f'\left( x \right) = - \left( {\pi + 4} \right)x + a,\,\,f'\left( x \right) = 0 \Leftrightarrow x = \dfrac{a}{{\pi + 4}}\)
Bảng biến thiên:
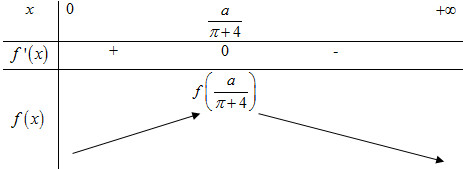
Vậy để diện tích cửa sổ là lớn nhất thì \(x = \dfrac{a}{{\pi + 4}} \Rightarrow d = 2x = \dfrac{{2a}}{{\pi + 4}}\).
Chọn: B







