Câu hỏi
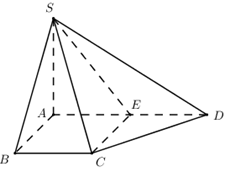
Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại \(A\)và \(B\). Biết \(SA \bot \left( {ABCD} \right)\), \(AB = BC = a\), \(AD = 2a\), \(SA = a\sqrt 2 \). Gọi \(E\) là trung điểm của \(AD\). Tính bán kính mặt cầu đi qua các điểm \(S\), \(A\), \(B\), \(C\), \(E\).
- A \(\frac{{a\sqrt 3 }}{2}\).
- B \(a\).
- C \(\frac{{a\sqrt 6 }}{3}\).
- D \(\frac{{a\sqrt {30} }}{6}\).
Phương pháp giải:
Khối chóp có cạnh bên vuông góc với đáy, sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp \(R = \sqrt {\frac{{{h^2}}}{4} + R_d^2} \) trong đó \(h\) là chiều cao khối chóp, \({R_d}\) là bán kính đường tròn ngoại tiếp đáy.
Lời giải chi tiết:
Xét tứ giác \(ABCE\) có \(AE//BC,\,\,AE = BC = a \Rightarrow ABCE\) là hình bình hành.
Lại có \(\angle BAE = {90^0}\,\left( {\,gt} \right),\,\,AB = BC \Rightarrow ABCE\) là hình vuông cạnh \(a\).
\( \Rightarrow \) Bán kính đường tròn ngoại tiếp hình vuông \(ABCE\) là \({R_d} = \frac{{a\sqrt 2 }}{2}\).
Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp \(S.ABCE\) là : \(R = \sqrt {\frac{{S{A^2}}}{4} + R_d^2} = \sqrt {\frac{{2{a^2}}}{4} + \frac{{2{a^2}}}{4}} = a\)
Chọn B.