Phương pháp giải:

Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp có các cạnh bên bằng nhau là \(R = \dfrac{{{{\left( {canh\,\,ben} \right)}^2}}}{{2h}}\) trong đó h là chiều cao của chóp.

Lời giải chi tiết:

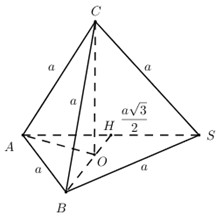
Ta có \(CA = CB = CS = a \Rightarrow \) Hình chiếu của \(C\) trên \(\left( {SAB} \right)\) trùng với tâm đường tròn ngoại tiếp \(\Delta SAB\).

Gọi \(O\) là tâm đường tròn ngoại tiếp \(\Delta SAB\) \( \Rightarrow SO \bot \left( {SAB} \right)\).

Gọi \(H\) là trung điểm của \(SA\). Tam giác \(SAB\) cân tại \(B \Rightarrow BH \bot SA \Rightarrow O \in BH\).

Ta có:

\(BH = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{4}} \right)}^2}}  = \dfrac{{a\sqrt {13} }}{4} \Rightarrow {S_{\Delta SAB}} = \dfrac{1}{2}BH.SA = \dfrac{1}{2}.\dfrac{{a\sqrt {13} }}{4}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt {39} }}{{16}}\).

Gọi \(R\) là bán kính ngoại tiếp \(\Delta SAB\) \( \Rightarrow R = \dfrac{{AB.SB.SA}}{{4{S_{\Delta ABC}}}} = \dfrac{{a.a.\dfrac{{a\sqrt 3 }}{2}}}{{4.\dfrac{{{a^2}\sqrt {39} }}{{16}}}} = \dfrac{{2a}}{{\sqrt {13} }} = OA\).

\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {{a^2} - \dfrac{{4{a^2}}}{{13}}}  = \dfrac{{3a}}{{\sqrt {13} }}\)

\( \Rightarrow {R_{cau}} = \dfrac{{{{\left( {canh\,\,ben} \right)}^2}}}{{2h}} = \dfrac{{{a^2}}}{{2.\dfrac{{3a}}{{\sqrt {13} }}}} = \dfrac{{a\sqrt {13} }}{6}\).

Chọn D.