Phương pháp giải:

Sử dụng định lý Ta-lét tính các tỉ lệ cạnh

Sử dụng tỉ số thể tích: Cho chóp \(S.ABC\) và các điểm \(D;E;F\) lần lượt thuộc các cạnh \(SA,SB,SC\). Khi đó ta có \(\dfrac{{{V_{S.DEF}}}}{{{V_{S.ABC}}}} = \dfrac{{SD}}{{SA}}.\dfrac{{SE}}{{SB}}.\dfrac{{SF}}{{SC}}\)

Lời giải chi tiết:

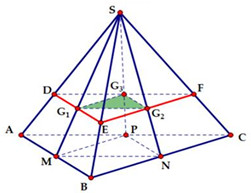
Gọi \(M,N,P\) lần lượt là trung điểm các cạnh \(AB,BC,AC\) và \({G_1};{G_2};{G_3}\) lần lượt là trọng tâm các tam giác \(SAB;SBC;SAC.\)

Theo tính chất trọng tâm ta có \(\dfrac{{S{G_1}}}{{SM}} = \dfrac{{S{G_2}}}{{SN}} = \dfrac{{S{G_3}}}{{SP}} = \dfrac{2}{3}\)

Trong \(\left( {SBC} \right)\), qua \({G_2}\) kẻ đường thẳng song song với \(BC\) cắt \(SB,SC\) lần lượt tại \(E\) và \(F.\)

Trong \(\left( {SAC} \right)\), đường thẳng \(F{G_3}\) cắt \(SA\) tại \(D.\)

Lúc này \(\left( {{G_1}{G_2}{G_3}} \right) \equiv \left( {DEF} \right)\)

Vì \(EF//BC \Rightarrow \dfrac{{SE}}{{SB}} = \dfrac{{SF}}{{SC}} = \dfrac{{S{G_2}}}{{SN}} = \dfrac{2}{3}\)  (theo định lý Ta-lét)

Lại có trong \(\Delta SPC\) có \(\dfrac{{S{G_3}}}{{SP}} = \dfrac{{SF}}{{SC}} = \dfrac{2}{3} \Rightarrow F{G_3}//PC \Rightarrow DF//BC \Rightarrow \dfrac{{SD}}{{SA}} = \dfrac{{SF}}{{SC}} = \dfrac{2}{3}\)

Từ đó ta có \(\dfrac{{{V_{S.DEF}}}}{{{V_{S.ABC}}}} = \dfrac{{SD}}{{SA}}.\dfrac{{SE}}{{SB}}.\dfrac{{SF}}{{SC}} = \dfrac{2}{3}.\dfrac{2}{3}.\dfrac{2}{3} = \dfrac{8}{{27}} \Rightarrow {V_{S.DEF}} = \dfrac{8}{{27}}V\)

Nên phần chứa đáy của hình chóp là \(V - \dfrac{8}{{27}}V = \dfrac{{19}}{{27}}V\)

Chọn C.